Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Преобразования графиков тригонометрических функций y=sinx и y=cosx
Содержание
- 1. Преобразования графиков тригонометрических функций y=sinx и y=cosx
- 2. Пристальное, глубокое изучение природы есть источник самых плодотворных открытий математики. Жан Батист Жозеф Фурье
- 3. «Синус» (от латинского sinus - «перегиб», которое,
- 4. p 3,14Назовите функции, графики которых изображены на
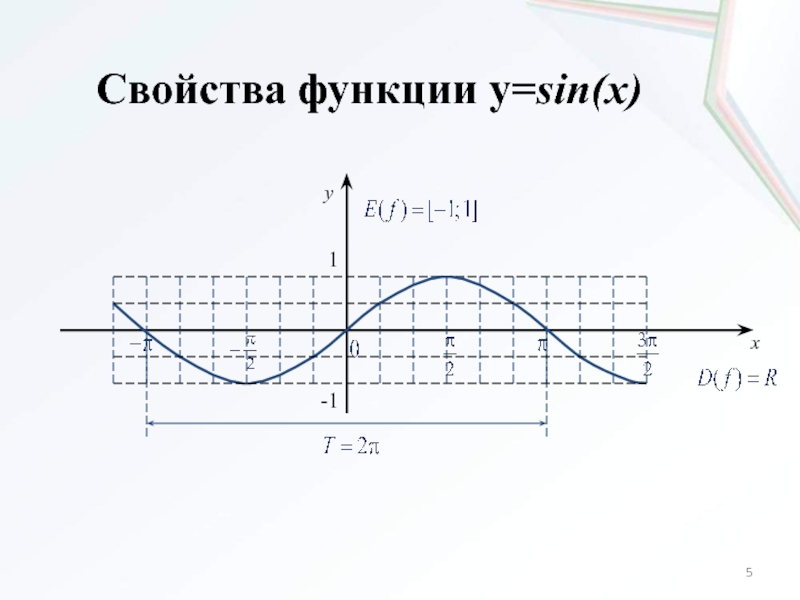
- 5. Свойства функции y=sin(x)xy1-1
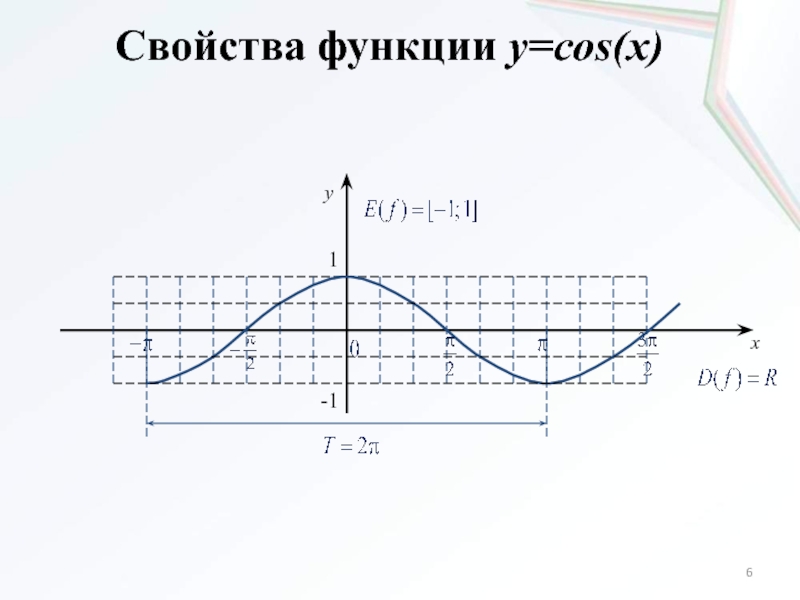
- 6. Свойства функции y=cos(x)xy1-1
- 7. Виды преобразований графиков функций y =
- 8. 1. Параллельный перенос вдоль оси Oy
- 9. yx0y=f(x)+bb0y=f(x)
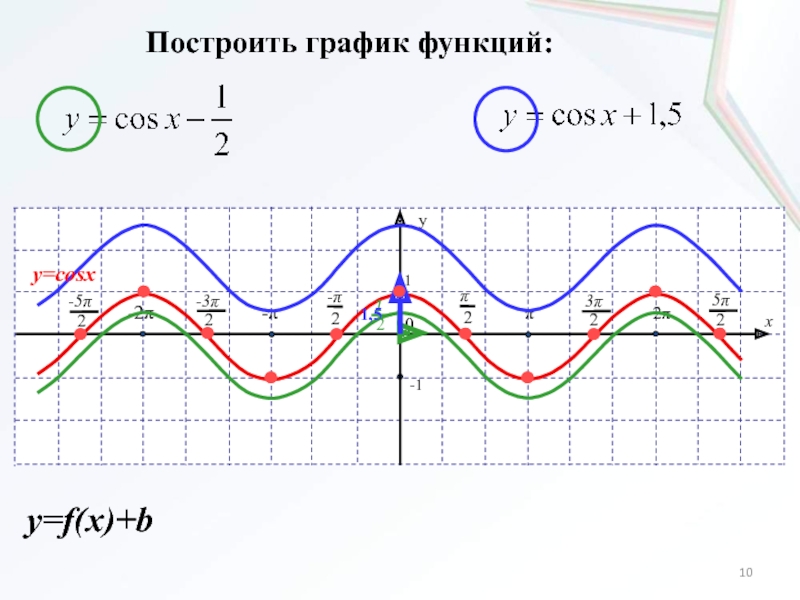
- 10. Построить график функций:y=cosxy=f(x)+b
- 11. 2. Параллельный перенос вдоль оси Ox
- 12. yx0y=f(x - а)а0а0y=f(x)
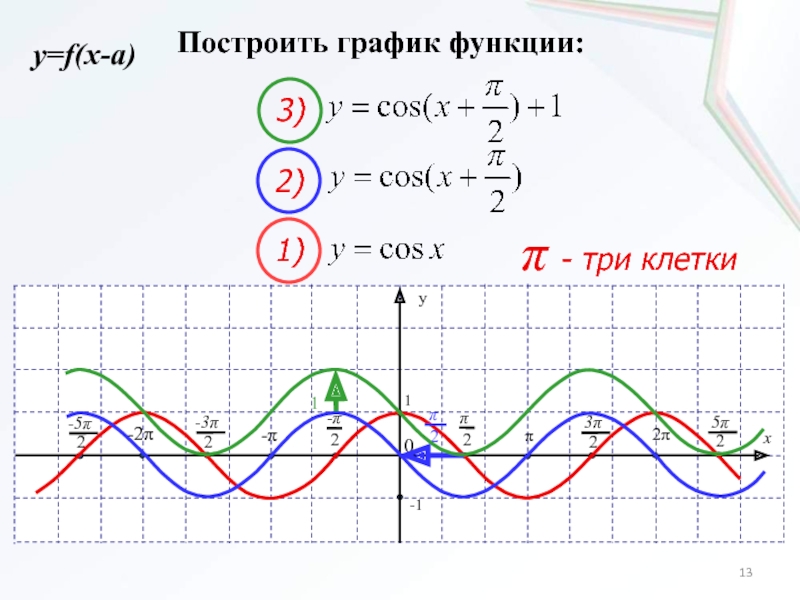
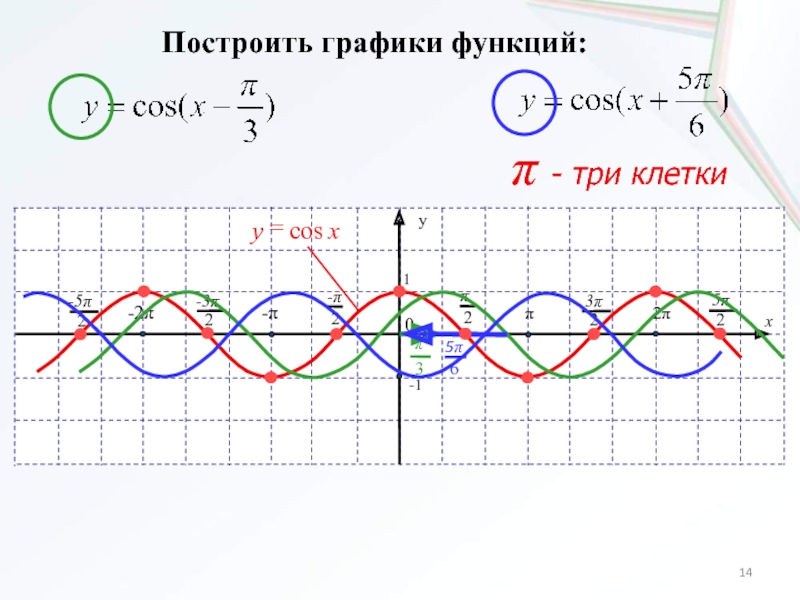
- 13. Построить график функции: p - три клетки2) 1) 3) y=f(x-a)
- 14. Построить графики функций:p - три клетки
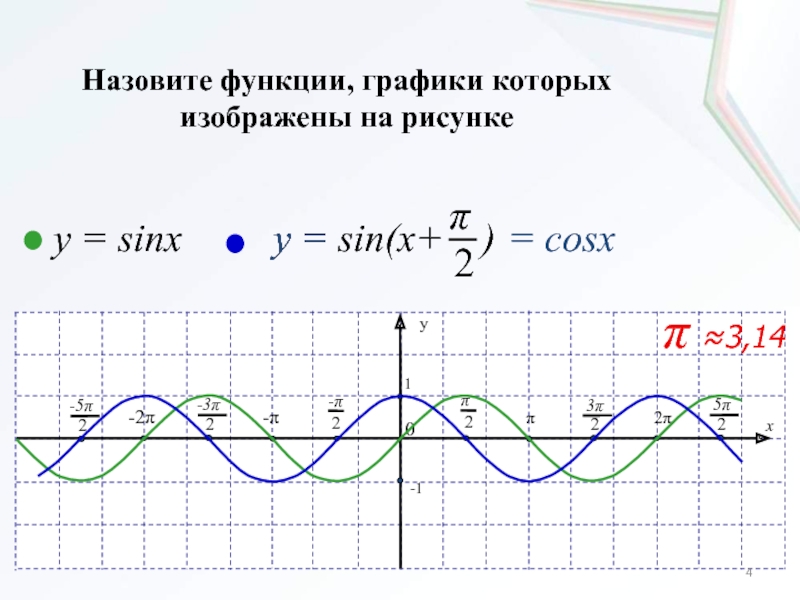
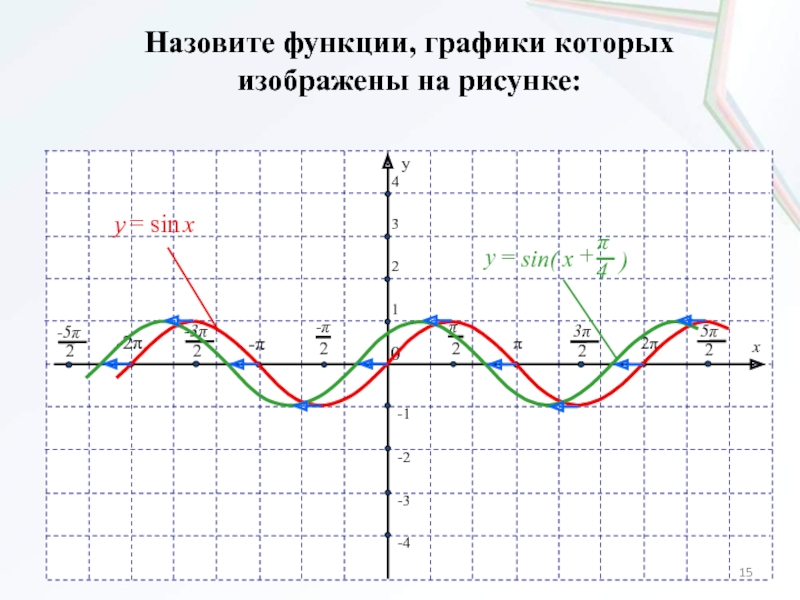
- 15. Назовите функции, графики которых изображены на рисунке:
- 16. 3. Растяжение (сжатие) в k раз
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. 4. Растяжение (сжатие) в k раз
- 22. Слайд 22
- 23. Слайд 23
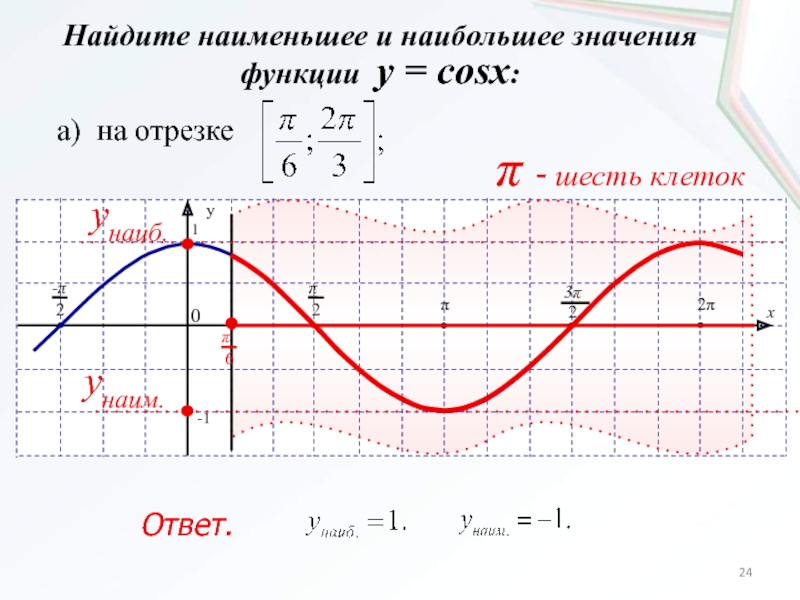
- 24. Найдите наименьшее и наибольшее значения функции y = cosx:а) на отрезке p - шесть клетокyнаиб.yнаим.Ответ.
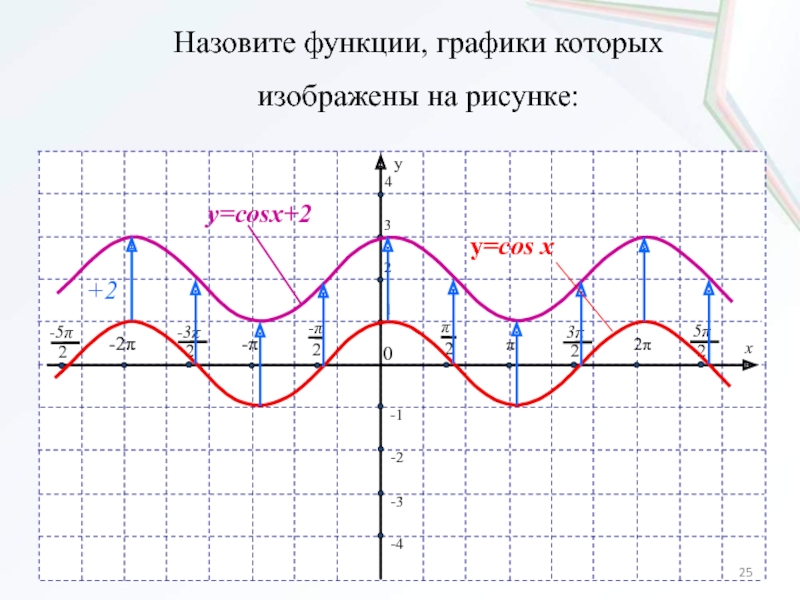
- 25. Назовите функции, графики которых изображены на рисунке:
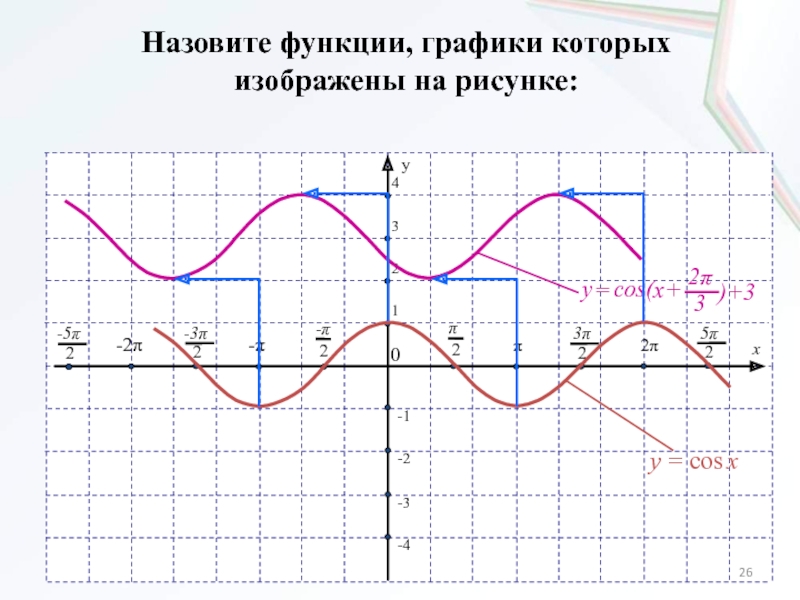
- 26. Назовите функции, графики которых изображены на рисунке:
- 27. Найдите наименьшее и наибольшее значения функции y
- 28. Практическая работаЗадания выполняются в программе Trigon;Максимальная оценка 5 баллов.
- 29. Постройте график функции и определите D(f), E(f)
- 30. Проверьте результат:1. у =7cos х1) (-∞; ∞)
- 31. Скачать презентанцию
Пристальное, глубокое изучение природы есть источник самых плодотворных открытий математики. Жан Батист Жозеф Фурье
Слайды и текст этой презентации
Слайд 1Преобразования графиков тригонометрических функций
y=sinx и y=cosx
Подготовила учитель математики
I категории
Н.В. Руцынская
Слайд 2Пристальное, глубокое изучение природы есть источник самых плодотворных открытий математики. Жан
Батист
Жозеф Фурье
Слайд 3«Синус»
(от латинского sinus - «перегиб», которое, в свою очередь,
происходит от арабского слова «джива» - «тетива лука»)
«Косинус»
(сокращение
словосочетания complementi sinus - «синус дополнения») «Тангенс»
(от латинского tangens - «касательная», «касательная к окружности»)
Слайд 7Виды преобразований графиков функций y = sinx и y =
cosx:
Параллельный перенос вдоль оси Oy;
Параллельный перенос вдоль оси Ox;
Растяжение (сжатие)
в k раз вдоль оси Oy;Растяжение (сжатие) в k раз вдоль оси Ox;
Пример построения графика сложной функции.
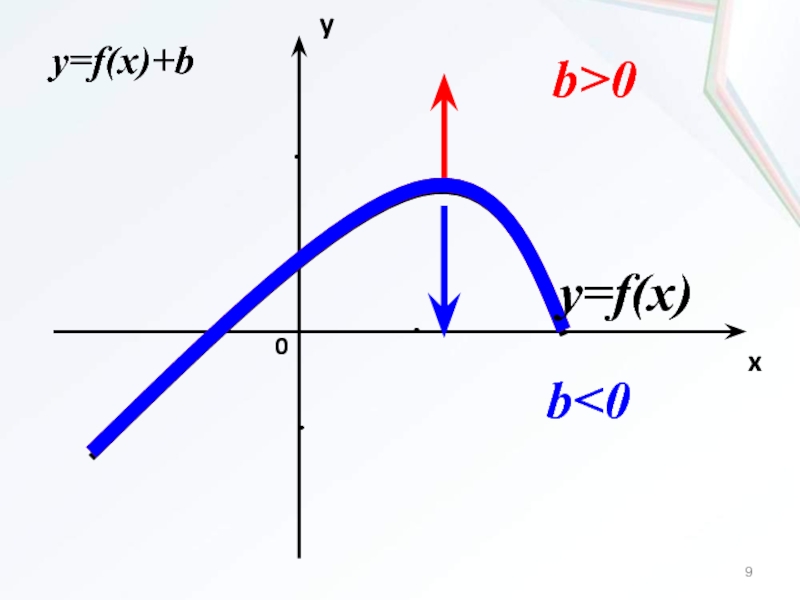
Слайд 81. Параллельный перенос
вдоль оси Oy
Для построения графика функции
y=f(x)+b, где b - const надо:
если b0, то перенести
график функции y=f(x) параллельно на b отрезков вверх вдоль оси Oy;если b0, то перенести график функции y=f(x) параллельно на b отрезков вниз вдоль оси Oy.
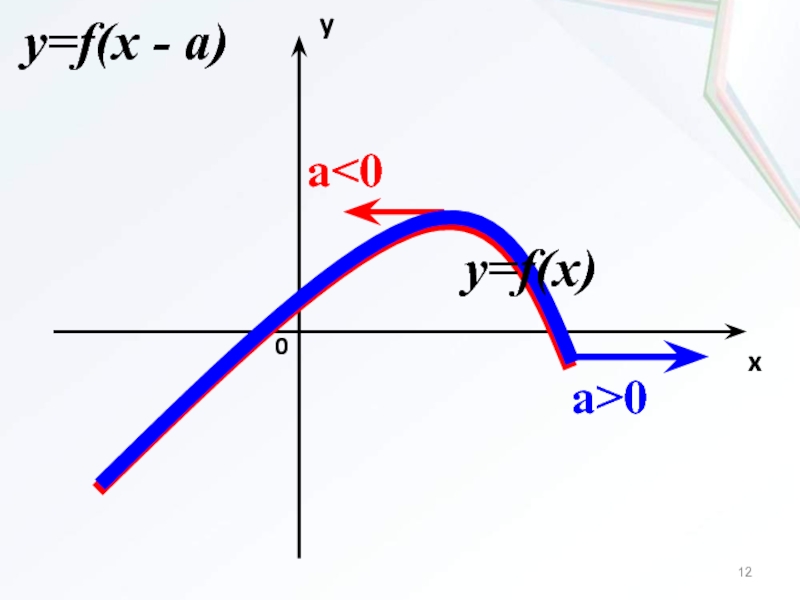
Слайд 112. Параллельный перенос
вдоль оси Ox
Для построения графика
функции y=f(x-a) надо:
если a0, то перенести график функции y=f(x)
вправо на а отрезков вдоль оси Ox;если a0, то перенести график функции y=f(x) влево на а отрезков вдоль оси Ox.
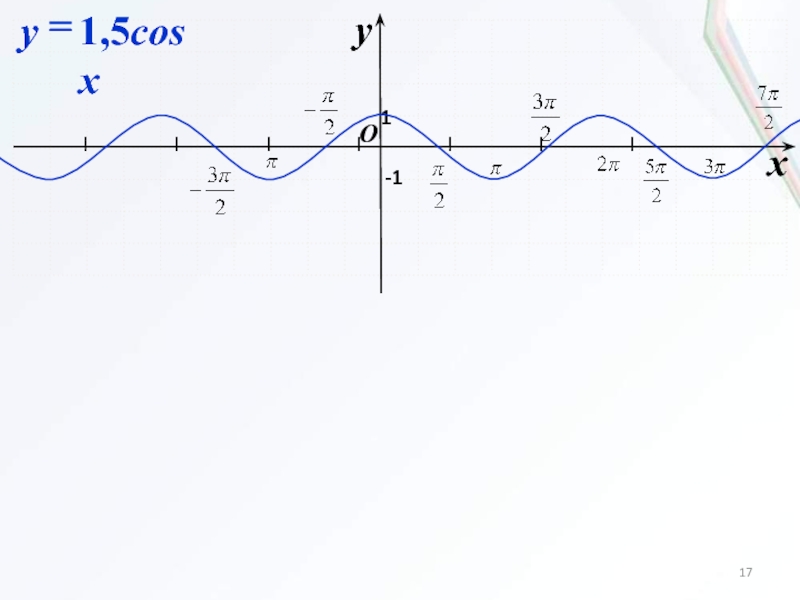
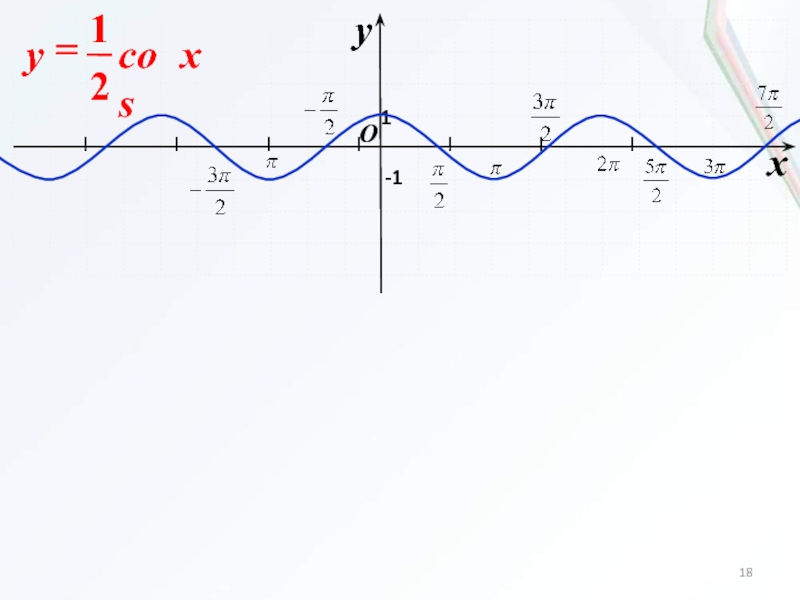
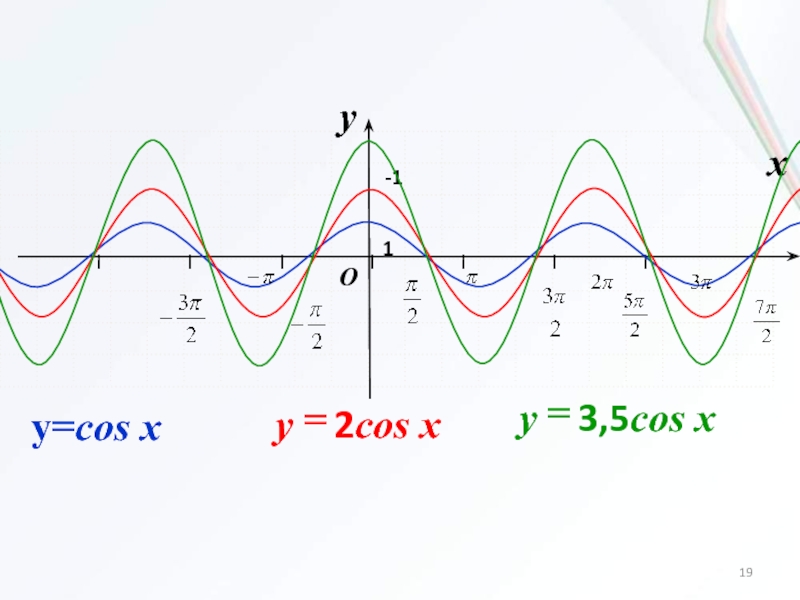
Слайд 163. Растяжение (сжатие)
в k раз вдоль оси Oy
Для построения графика функции y=kf(x) надо:
если k0, то растянуть
график функции y=f(x) в k раз вдоль оси Oy;если 0k1, то сжать график функции y=f(x) в k раз вдоль оси Oy.
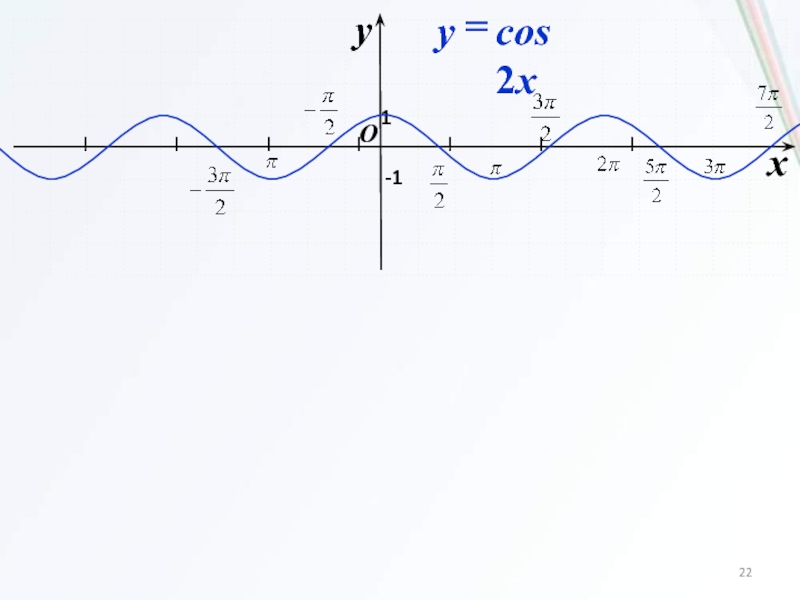
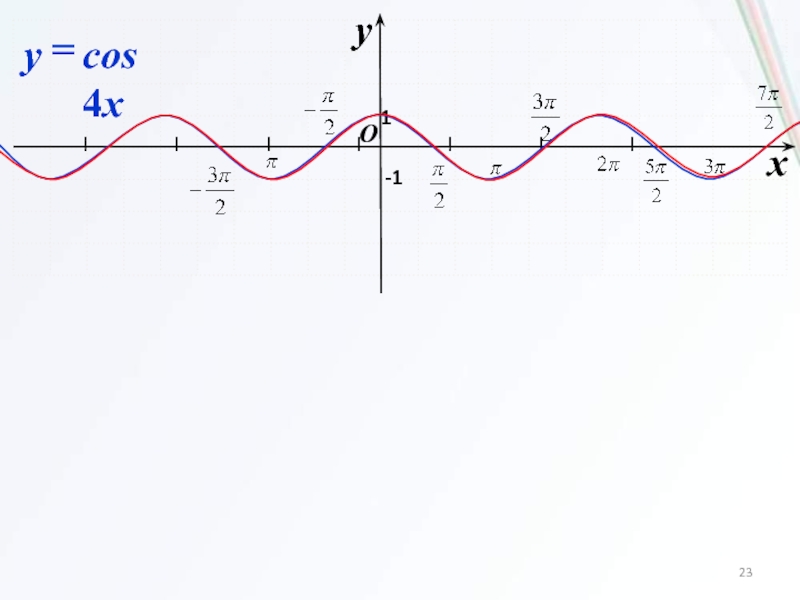
Слайд 214. Растяжение (сжатие)
в k раз вдоль оси Ox
Для построения графика функции y=f(x/k) надо подвергнуть график функции f
растяжению с коэффициентом k вдоль оси Ox.
Слайд 24Найдите наименьшее и наибольшее значения функции y = cosx:
а) на
отрезке
p - шесть клеток
yнаиб.
yнаим.
Ответ.
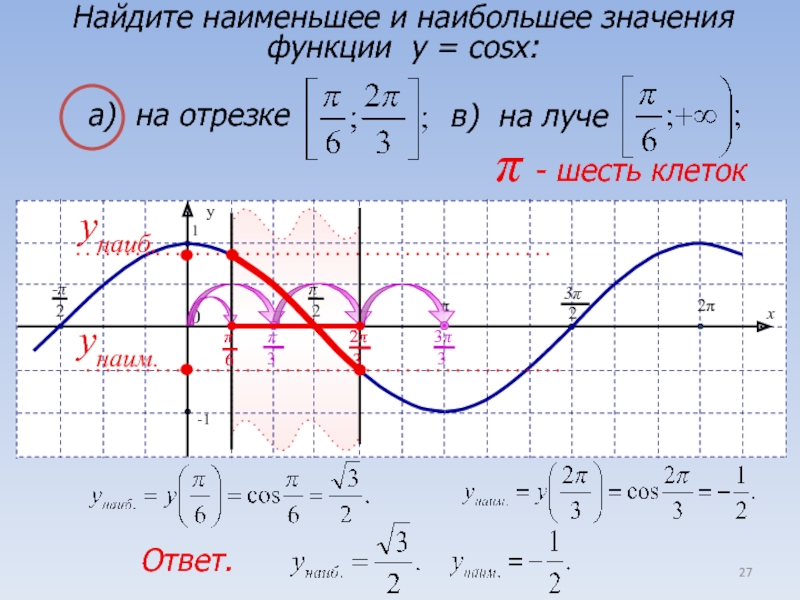
Слайд 27Найдите наименьшее и наибольшее значения функции y = cosx:
а) на
отрезке
в) на луче
p - шесть клеток
yнаиб.
yнаим.
Ответ.
Слайд 29Постройте график функции и определите D(f), E(f) и T:
1. у
=7cos х
1) (-∞; ∞) 2) [ 0;
7] 3) [-1; 1] 4) [-7; 7]
1. у = - 4cos x
1) [-1; 1] 2) [ -4; 0]
3) [-4; 4] 4) (-∞; ∞)
2. y = 9sin х
1) [-1; 1] 2) [ 8;10]
3) [-9; 9] 4) [0; 9]
2. у =cos 2x
1) [-1/2; 1/2] 2) [ 0; 2]
3) [-2; 2] 4) [-1; 1]
3. y = 7sin2 x
1) [-7; 7] 2) (-∞; ∞)
3) [-3,5; 3,5] 4) [- 2/7; 2/7]
3. y = sin x – 2
1) [ -3; -1] 2) (-∞; ∞)
3) [-1; 1] 4) [-3; 0]
4. y = 3sin x/2 – 4
1) [-1,5; 1,5] 2) [ -3; 3]
3) (-3; 3) 4) [-1; 1]
4. y = - 1/5sin 2x
1) [-1; 1] 2) [ -2/5; 2/5]
3) [-1/5; 1/5] 4) (-1; 1)
5. у = cos x + 3
1) [ 0; 4] 2) [-1; 1]
3) [ 2; 4] 4) [0; 3]
5. y = 3sin x +2
1) [ -3; 5] 2) [2; 5]
3) [ -1; 5] 4) [-3; 3]
1 вариант
2 вариант
Слайд 30Проверьте результат:
1. у =7cos х
1) (-∞; ∞)
2) [ 0; 7]
3) [-1; 1]
4) [-7; 7]1. у = - 4cos x
1) [-1; 1] 2) [ -4; 0]
3) [-4; 4] 4) (-∞; ∞)
2. y = 9sin х
1) [-1; 1] 2) [ 8;10]
3) [-9; 9] 4) [0; 9]
2. у = cos 2x
1) [-1/2; 1/2] 2) [ 0; 2]
3) [-2; 2] 4) [-1; 1]
3. y = 7sin2 x
1) [-7; 7] 2) (-∞; ∞)
3) [-3,5; 3,5] 4) [- 2/7; 2/7]
3. y = sin x – 2
1) [ -3; -1] 2) (-∞; ∞)
3) [-1; 1] 4) [-3; 0]
4. y = 3sin x/2 – 4
1) [-1,5; 1,5] 2) [ -3; 3]
3) (-3; 3) 4) [-7; -1]
4. y = - 1/5sin 2x
1) [-1; 1] 2) [ -2/5; 2/5]
3) [-1/5; 1/5] 4) (-1; 1)
5. у = cos x + 3
1) [ 0; 4] 2) [-1; 1]
3) [ 2; 4] 4) [0; 3]
5. y = 3sin x +2
1) [ -3; 5] 2) [2; 5]
3) [ -1; 5] 4) [-3; 3]
1 вариант
2 вариант
![Проверьте результат:1. у =7cos х1) (-∞; ∞) 2) [ 0; 7] 3) [-1;](/img/thumbs/ea068c553b47a629d4f4a6b00fa8533a-800x.jpg "Преобразования графиков тригонометрических функций y=sinx и y=cosx Проверьте результат:1. у =7cos х1) (-∞; ∞) 2) [ 0;")
