Равнобедренный треугольник (7 класс)

Содержание

1. Равнобедренный треугольник (7 класс)
2. Цель урока: ввести определение равнобедренного
3. Отгадайте ребус Треугольник
4. Из трёх точек состоит из века в
5. Классификация треугольников по величине углов Узнает
6. Равенство треугольниковКакое условие необходимо добавить, чтобы доказать равенство треугольников по первому признаку равенства треугольников.21
7. Треугольник – самая простая замкнутаяпрямолинейная фигура,
8. Треугольник называется
9. Равнобедренный треугольникВ равнобедренном треугольнике АМК АМ
10. Какие из треугольников, изображённых на рисунке, являются
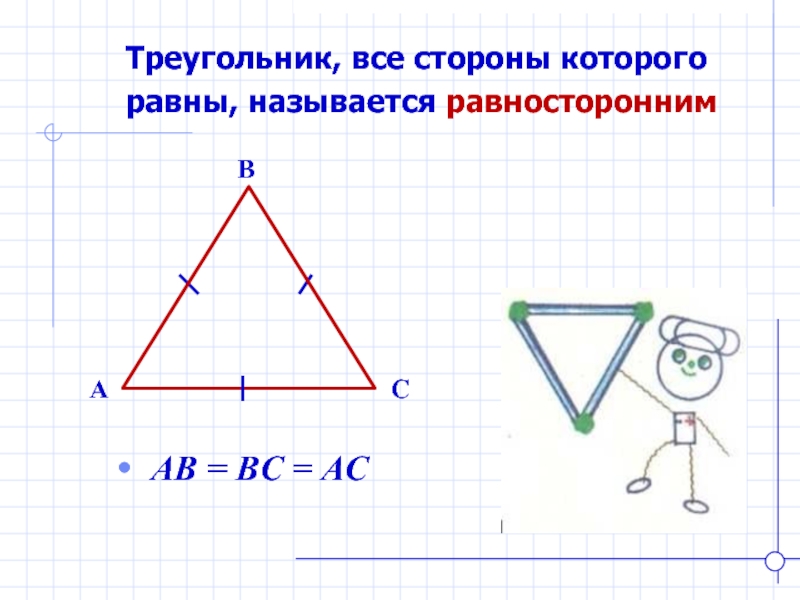
11. Треугольник, все стороны которого
12. Зовусь я треугольник, Со мной хлопот
13. KNMПеречислите равные элементы треугольников, если ∆CDE =
14. Теорема. В равнобедренном треугольнике углы при основании
15. Решение задач В равнобедренном треугольнике
16. Решение задачНайдите угол KBA.ےKBA = 70° ےKBA = 40° ےKBA = 110°12 3
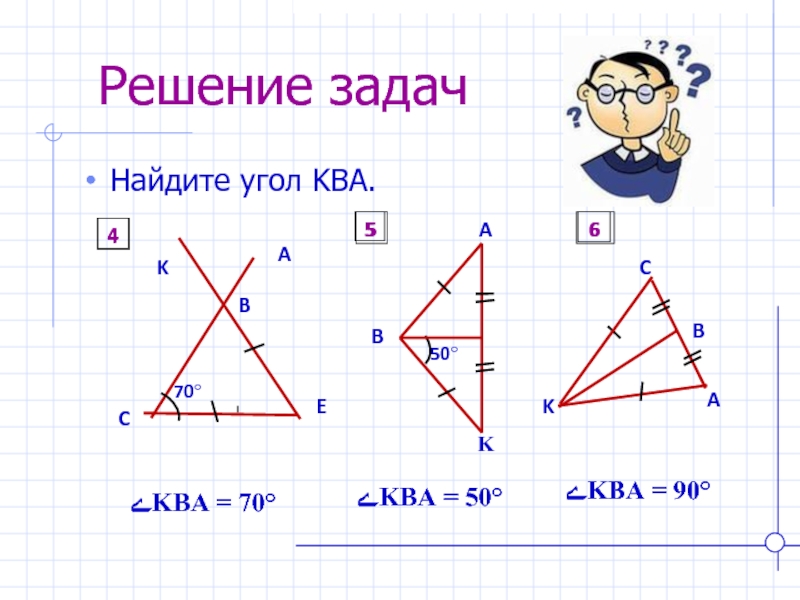
17. Решение задачНайдите угол KBA.ےKBA = 70°ےKBA = 50° ےKBA = 90°456
18. Решение задачДокажите, что ∆
19. Решение задачAFB = ∆ CFD. Докажите, что ∆ AFD – равнобедренный.
20. Решение задач ∆ ABC -равнобедренный,
21. Контрольные вопросыКакой треугольник называется равнобедренным?Какой треугольник называется
22. Домашнее заданиеИзучить
23. Удачи!
24. Информационные источники
25. Скачать презентанцию

Цель урока: ввести определение равнобедренного треугольника и его элементов; познакомится со свойством углов равнобедренного треугольника;научиться пользоваться доказанным свойством при решении задач.

Главная
Математика
Равнобедренный треугольник (7 класс)

Слайды и текст этой презентации

Слайд 1Равнобедренный треугольник
Геометрия 7 класс
Яковлева Любовь Викторовна
МБОУ «Самосдельская СОШ им. Шитова

В. А.»

Слайд 2 Цель урока:
ввести определение равнобедренного треугольника и

его элементов;
познакомится со свойством углов равнобедренного треугольника;
научиться пользоваться

доказанным свойством при решении задач.

Цель урока: ввести определение равнобедренного треугольника и его элементов; познакомится со свойством углов

Слайд 3 Отгадайте ребус
Треугольник

Слайд 4Из трёх точек состоит из века в век,

Потому что

так придумал человек.
Не лежат при этом точки на прямой,
Хоть и хочется друг к другу им домой.
Три отрезка их всю жизнь соединяют.
И вершинами те точки называют,
А отрезки сторонами величают.

Треугольник

Слайд 5Классификация треугольников по величине углов
Узнает очень просто меня

любой дошкольник.
Я тупо -, прямо -, остро – угольный

треугольник.

Остроугольные
Тупоугольные
Прямоугольные

Слайд 6Равенство треугольников
Какое условие необходимо добавить, чтобы доказать равенство треугольников по

первому признаку равенства треугольников.

2
1

Равенство треугольниковКакое условие необходимо добавить, чтобы доказать равенство треугольников по первому признаку равенства треугольников.21

Слайд 7 Треугольник – самая простая замкнутая
прямолинейная фигура, одна из первых,
свойства

которой человек узнал ещё в
глубокой древности. Например, то, что в
равнобедренном

треугольнике углы при
основании равны, было известно ещё
древним вавилонянам 4000 лет назад.
Равнобедренный треугольник обладает
ещё рядом геометрических свойств,
которые всегда имели широкое
применение в практической жизни.

Треугольник – самая простая замкнутаяпрямолинейная фигура, одна из первых,свойства которой человек узнал ещё вглубокой древности. Например,

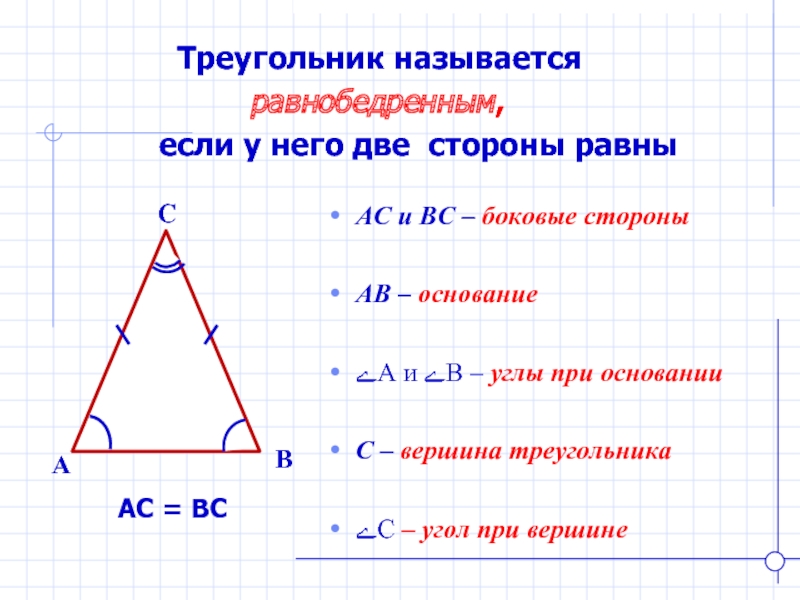
Слайд 8 Треугольник называется

равнобедренным,
если

у него две стороны равны

АС и ВС – боковые стороны

АВ – основание

ےА и ےВ – углы при основании

С – вершина треугольника

ےС – угол при вершине

АС = ВС

Слайд 9Равнобедренный треугольник
В равнобедренном треугольнике АМК АМ = АК. Назовите

основание и углы при основании этого треугольника.

(МК, ےМ, ےК)
Дан равнобедренный треугольник СОР c основанием СР. Назовите боковые стороны и углы при основании этого треугольника.
(СО и ОР, ےС, ےР)

Слайд 10Какие из треугольников, изображённых на рисунке, являются равнобедренными, почему?

У равнобедренных треугольников назовите: боковые стороны, основание, углы при основании,

угол, противолежащий основанию (угол при вершине равнобедренного треугольника).

Какие из треугольников, изображённых на рисунке, являются равнобедренными, почему? У равнобедренных треугольников назовите: боковые стороны, основание,

Слайд 11 Треугольник, все стороны которого
равны,

называется равносторонним

B
A
C
АВ = ВС = АС

Треугольник, все стороны которого равны, называется равносторонним BAC АВ =

Слайд 12 Зовусь я треугольник,
Со мной хлопот не оберётся

школьник …
По – разному всегда я называюсь,
Бываю я

равносторонним, когда все стороны равны.
Когда ж все разные даны, то я зовусь разносторонним.
И если, наконец, равны две стороны,
То равнобедренным я величаюсь.

Классификация треугольников по сторонам:
разносторонние,
равнобедренные,
равносторонние.

Зовусь я треугольник, Со мной хлопот не оберётся школьник … По – разному всегда я называюсь,

Слайд 13K
N
M

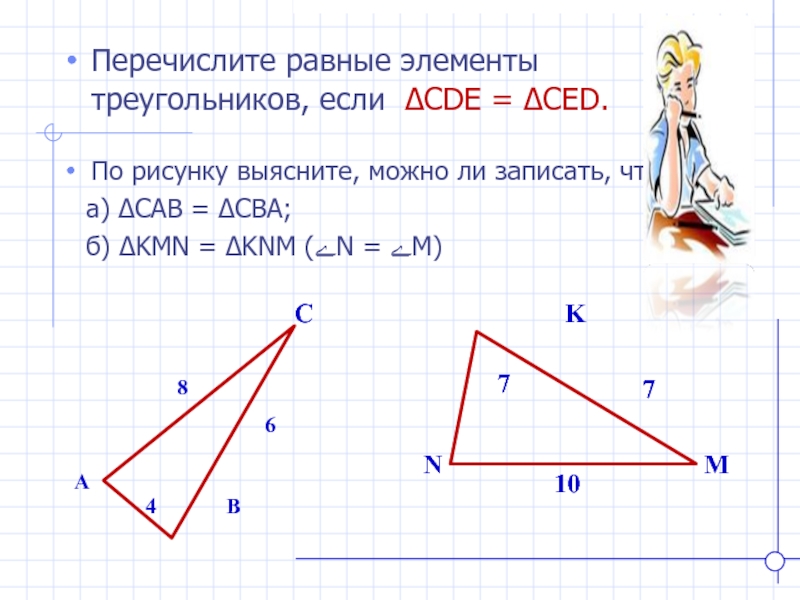
Перечислите равные элементы треугольников, если ∆CDE = ∆CED.

A
B
C
4
8
6
7
7
10
По рисунку выясните,

можно ли записать, что:
а) ∆CAB = ∆CBA;

б) ∆KMN = ∆KNM (ےN = ےM)

KNMПеречислите равные элементы треугольников, если ∆CDE = ∆CED.ABC4867710По рисунку выясните, можно ли записать, что: а) ∆CAB

Слайд 14Теорема. В равнобедренном треугольнике углы при основании равны.

Дано: ∆ABC,

CA = CB.
Доказать: в ∆ ABC ےA = ےB.

Доказательство.
∆CAB = ∆CBA по двум сторонам
и углу между ними. Действительно,
у них CA = CB, CB = CA по условию,
угол при вершине С – общий.
Из равенства треугольников
следует равенство соответствующих
углов, т. е. ے А = ےВ.
Теорема доказана.

Теорема. В равнобедренном треугольнике углы при основании равны. Дано: ∆ABC, CA = CB. Доказать: в ∆ ABC

Слайд 15 Решение задач
В равнобедренном треугольнике боковая сторона равна

9см, а основание 5см. Вычислите периметр треугольника.
В равнобедренном треугольнике основание

равно 7см, а периметр равен 17см. Вычислите боковую сторону треугольника.
В равнобедренном треугольнике боковая сторона равна 6см, а периметр 22см. Вычислите основание треугольника.
В равностороннем треугольнике периметр равен 21см. Вычислите сторону треугольника.

Решение задач В равнобедренном треугольнике боковая сторона равна 9см, а основание 5см. Вычислите периметр треугольника.В

Слайд 16 Решение задач
Найдите угол KBA.

ےKBA = 70°
ےKBA = 40°

ےKBA = 110°
1
2
3

Слайд 17 Решение задач
Найдите угол KBA.

ےKBA = 70°
ےKBA = 50°

ےKBA = 90°
4
5
6

Слайд 18 Решение задач
Докажите, что
∆ BAM = ∆

BCN. Определите вид
∆ BMN.

Решение задачДокажите, что ∆ BAM = ∆ BCN. Определите вид ∆

Слайд 19 Решение задач
AFB = ∆ CFD. Докажите, что
∆

AFD – равнобедренный.

Слайд 20 Решение задач
∆ ABC -равнобедренный,
∆BCD -

равносторонний.
P∆ABC = 40см,
P∆BCD = см.

Найдите AB и BC.

Решение задач ∆ ABC -равнобедренный, ∆BCD - равносторонний. P∆ABC = 40см,

Слайд 21Контрольные вопросы
Какой треугольник называется равнобедренным?
Какой треугольник называется равносторонним?
Является ли равносторонний

треугольник равнобедренным?
Каким свойством обладают углы в равнобедренном треугольнике?

Контрольные вопросыКакой треугольник называется равнобедренным?Какой треугольник называется равносторонним?Является ли равносторонний треугольник равнобедренным?Каким свойством обладают углы в равнобедренном

Слайд 22 Домашнее задание
Изучить п. 23.
Контрольные вопросы

3 – 5 на стр. 37.
Выполнить упр. 9, 10 на

стр. 39.

Домашнее заданиеИзучить п. 23.Контрольные вопросы 3 – 5 на стр. 37.Выполнить упр.

Слайд 23 Удачи!

Слайд 24Информационные источники

Литература.

Погорелов А.В. Геометрия: учебник для 7 – 9 кл. общеобразовательных учреждений/ А. В. Погорелов. М.: Просвещение, 2010.
Геометрия. 7 класс: поурочные планы по учебнику А. В. Погорелова/
авт. – сост. Е. П. Моисеева.- Волгоград: Учитель, 2006.
Геометрия в 6 классе: Пособие для учителей/ Н. Б. Мельникова, И. Л. Никольская, Л. Ю. Чернышева. – М.: Просвещение, 1982.
Геометрия. Рабочая тетрадь для 7 класса/Мищенко Т. М. – М.:
Издательский Дом «Генжер»,2000.
Тематический контроль по геометрии. 7 -9 класс/Мищенко Т. М. – М.: Издательский Дом «Генжер», 1997

Интернет – ресурсы.
www.testent.ru
http://www.uchportal.ru/load/24-1-0-22420
festival.1september.ru/articles/534282/

Скачать презентацию

Теги

Разделы презентаций

Равнобедренный треугольник (7 класс)

Содержание

Слайды и текст этой презентации

Слайд 1Равнобедренный треугольникГеометрия 7 классЯковлева Любовь ВикторовнаМБОУ «Самосдельская СОШ им. Шитова

В. А.»

Слайд 2 Цель урока: ввести определение равнобедренного треугольника и

его элементов; познакомится со свойством углов равнобедренного треугольника;научиться пользоваться

Слайд 3 Отгадайте ребус Треугольник

Слайд 4Из трёх точек состоит из века в век,

Потому что

Слайд 5Классификация треугольников по величине углов Узнает очень просто меня

любой дошкольник. Я тупо -, прямо -, остро – угольный

Слайд 6Равенство треугольниковКакое условие необходимо добавить, чтобы доказать равенство треугольников по

первому признаку равенства треугольников.21

Слайд 7 Треугольник – самая простая замкнутаяпрямолинейная фигура, одна из первых,свойства

которой человек узнал ещё вглубокой древности. Например, то, что вравнобедренном

Слайд 8 Треугольник называется

равнобедренным, если

Слайд 9Равнобедренный треугольникВ равнобедренном треугольнике АМК АМ = АК. Назовите

основание и углы при основании этого треугольника.

Слайд 10Какие из треугольников, изображённых на рисунке, являются равнобедренными, почему?

У равнобедренных треугольников назовите: боковые стороны, основание, углы при основании,

Слайд 11 Треугольник, все стороны которого равны,

называется равносторонним BAC АВ = ВС = АС

Слайд 12 Зовусь я треугольник, Со мной хлопот не оберётся

школьник … По – разному всегда я называюсь, Бываю я

Слайд 13KNMПеречислите равные элементы треугольников, если ∆CDE = ∆CED.ABC4867710По рисунку выясните,

можно ли записать, что: а) ∆CAB = ∆CBA;

Слайд 14Теорема. В равнобедренном треугольнике углы при основании равны. Дано: ∆ABC,

CA = CB. Доказать: в ∆ ABC ےA = ےB.

Слайд 15 Решение задач В равнобедренном треугольнике боковая сторона равна

9см, а основание 5см. Вычислите периметр треугольника.В равнобедренном треугольнике основание

Слайд 16 Решение задачНайдите угол KBA.ےKBA = 70° ےKBA = 40°

ےKBA = 110°12 3

Слайд 17 Решение задачНайдите угол KBA.ےKBA = 70°ےKBA = 50°

ےKBA = 90°456

Слайд 18 Решение задачДокажите, что ∆ BAM = ∆

BCN. Определите вид ∆ BMN.

Слайд 19 Решение задачAFB = ∆ CFD. Докажите, что ∆