Разные задачи повышенного уровня сложности на многогранники, цилиндры, косинус и шар

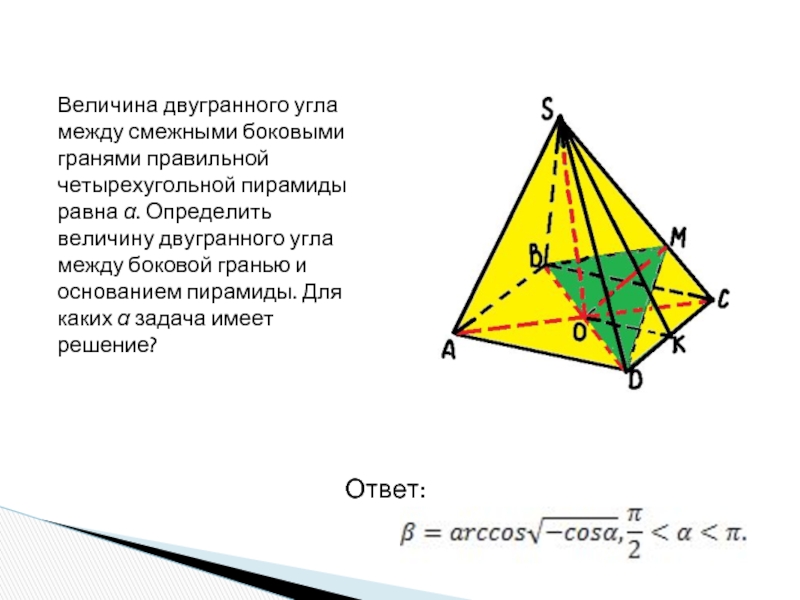
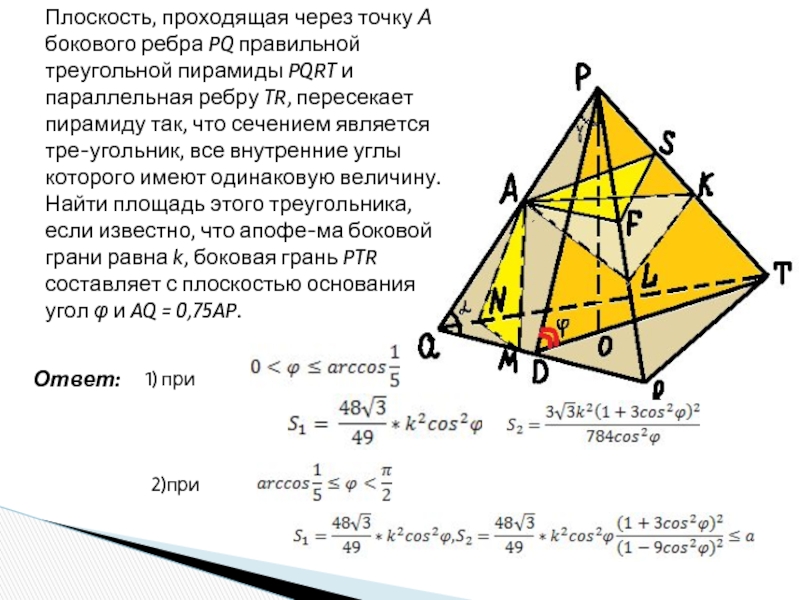
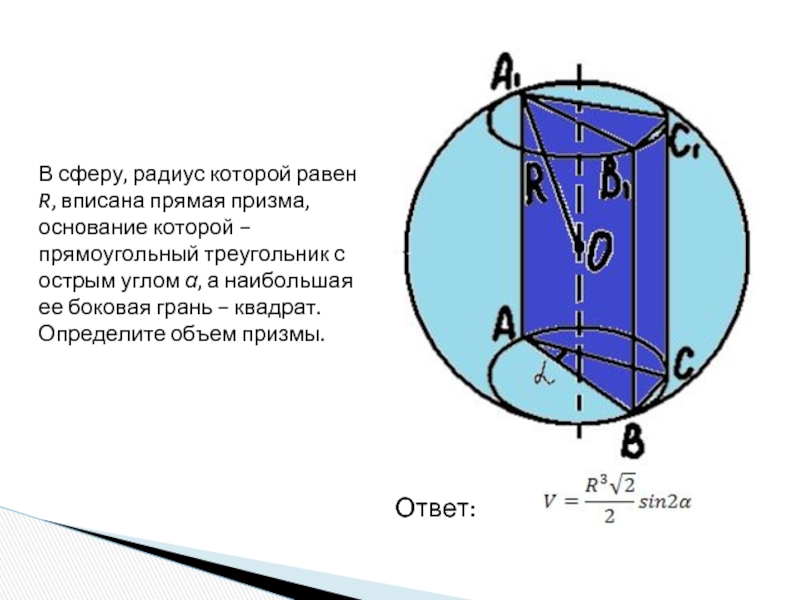
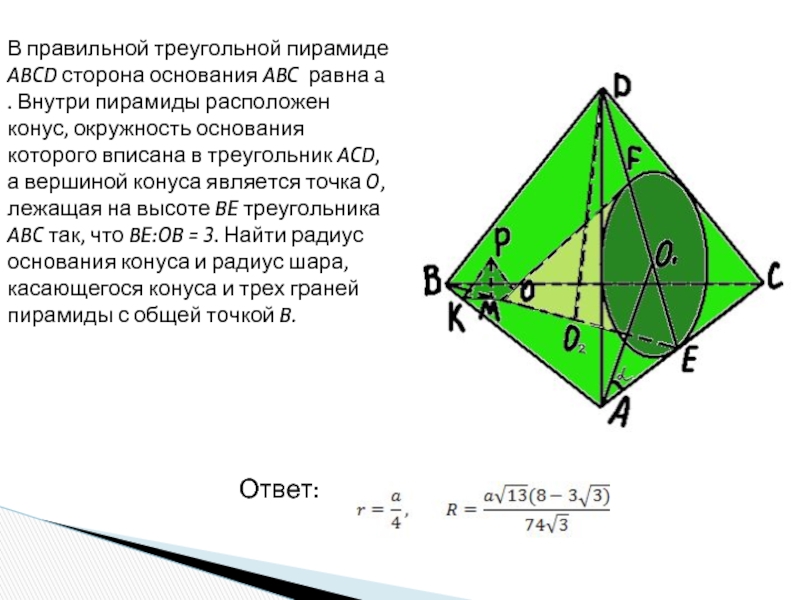
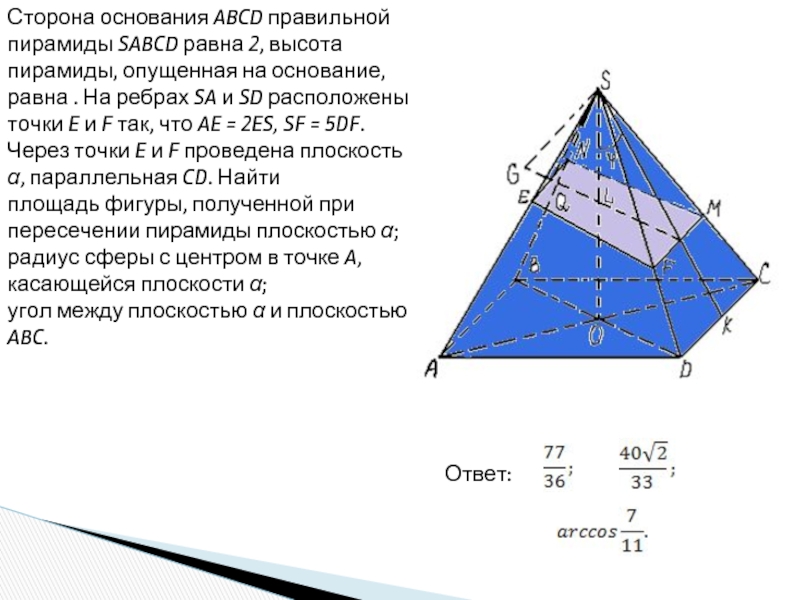
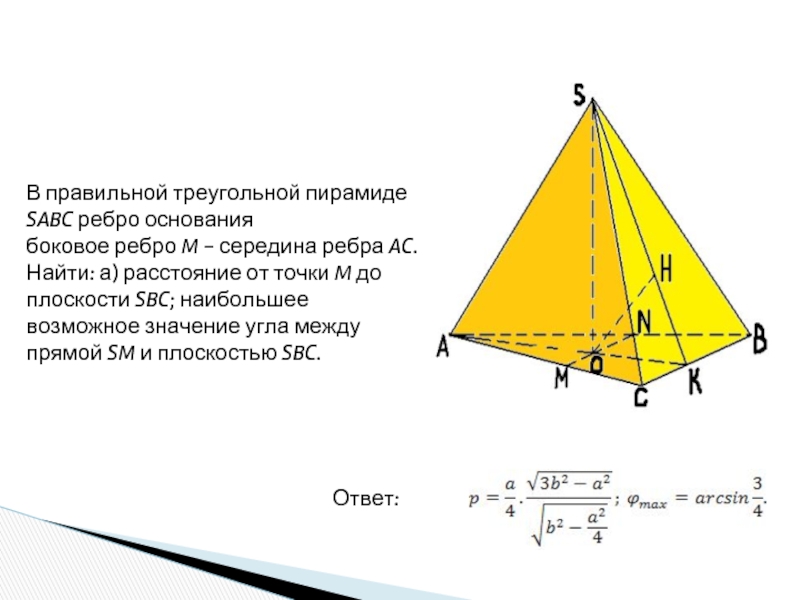
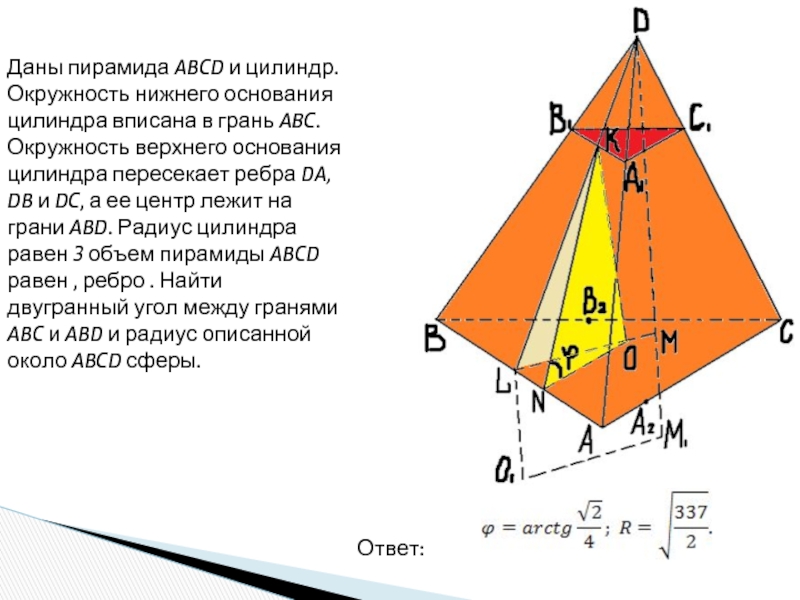
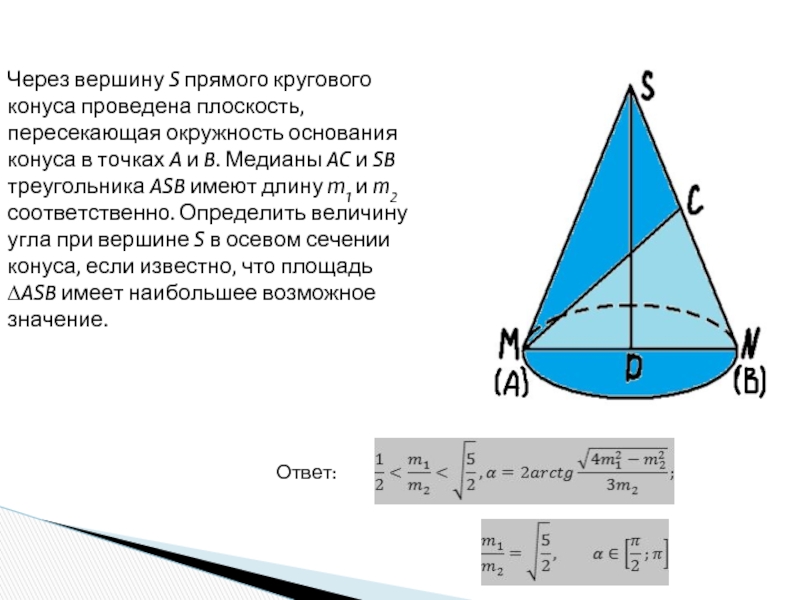
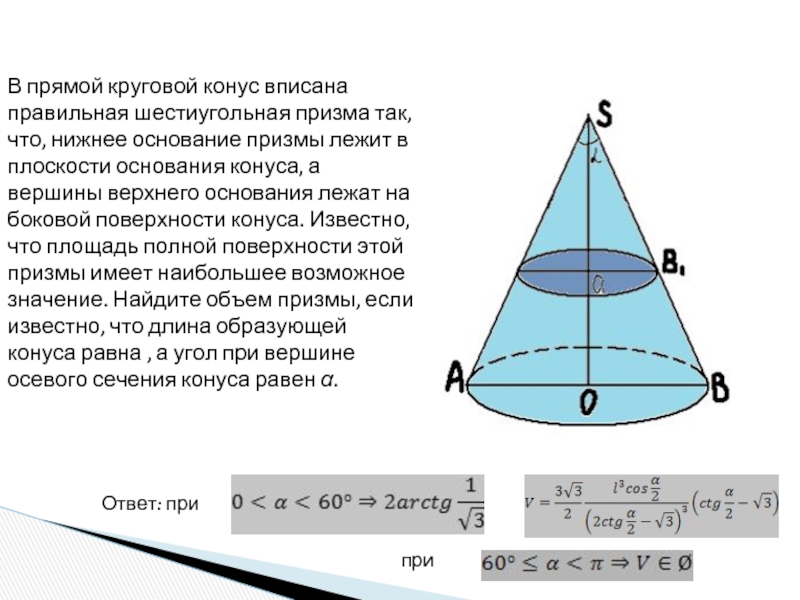
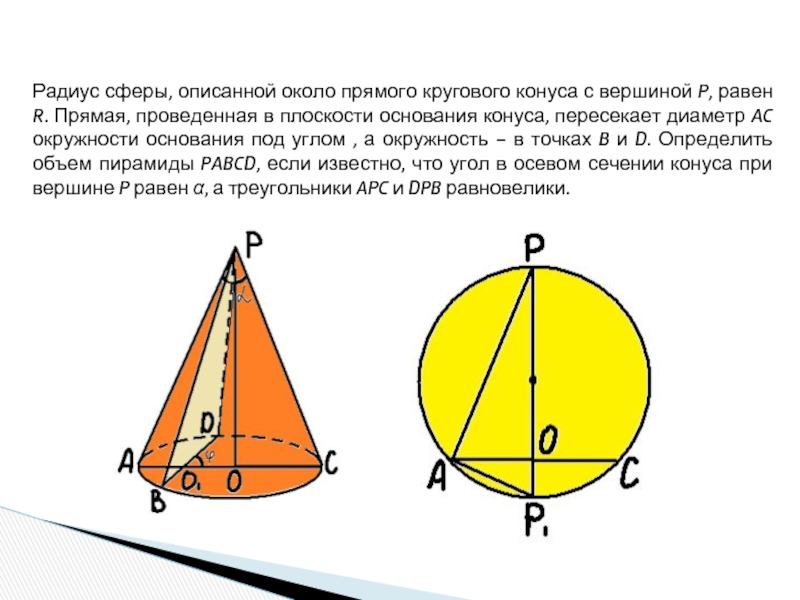
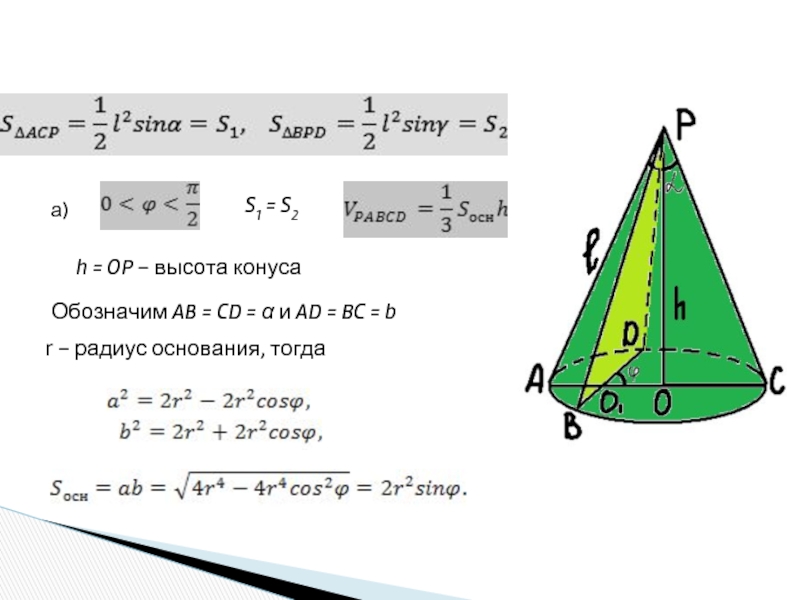
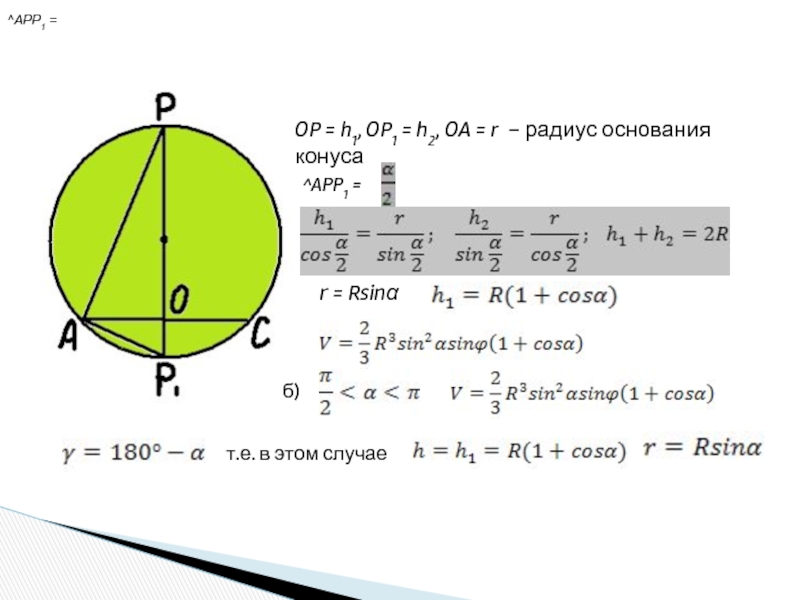
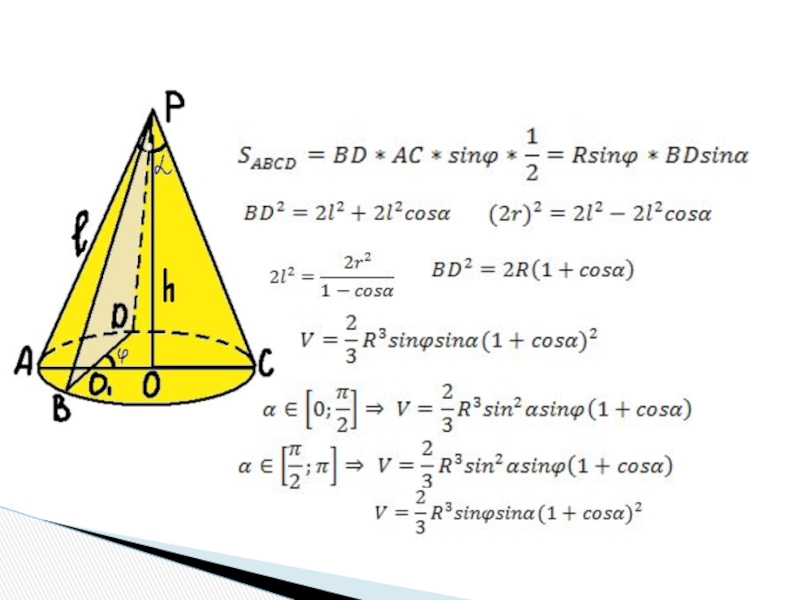
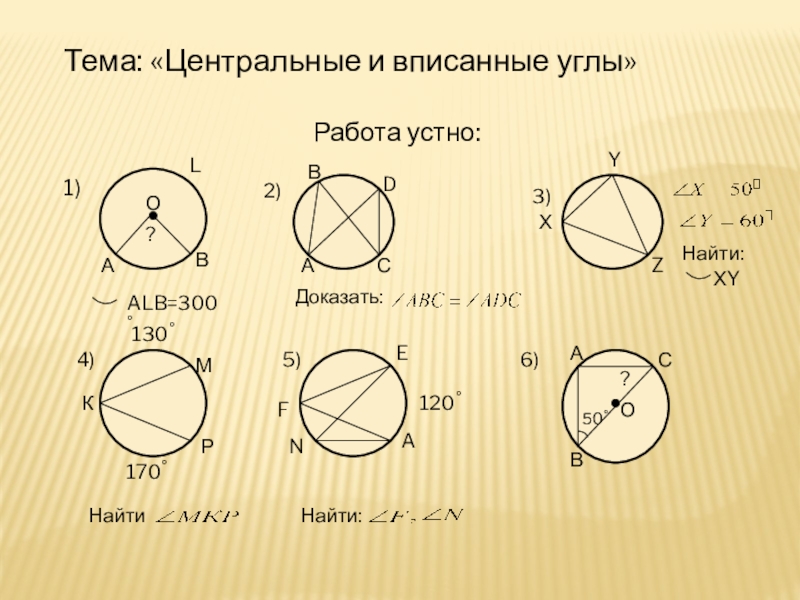
шар.
Выполнил:

ученик 10 «Б» класса
МБОУ лицей №3 г. Воронежа
Козловский Никита.

Руководитель:
Орлова О.В.
учитель высшей категории,
учитель математики
МОУ СОШ с углубленным изучением отдельных предметов
№78 городского округа город Воронеж

равна α. Определить величину двугранного угла между боковой гранью и

основанием пирамиды. Для каких α задача имеет решение?

Ответ:

пирамиды PQRT и параллельная ребру TR, пересекает пирамиду так, что

сечением является тре­угольник, все внутренние углы которого имеют одинаковую величину. Найти площадь этого треугольника, если известно, что апофе­ма боковой грани равна k, боковая грань PTR составляет с плоскостью основания угол φ и AQ = 0,75AP.

Ответ:

2)при

1) при

которой – прямоугольный треугольник с острым углом α, а наибольшая

ее боковая грань – квадрат. Определите объем призмы.

Ответ:

. Внутри пирамиды расположен конус, окружность основания которого вписана в

треугольник ACD, а вершиной конуса является точка O, лежащая на высоте BE треугольника ABC так, что BE:OB = 3. Найти радиус основания конуса и радиус шара, касающегося конуса и трех граней пирамиды с общей точкой B.

Ответ:

ребра AB, точка E лежит на ребре CD и EC:ED

= 1:2, точка F – центр грани ABC. Найти угол между прямыми КC и KE, расстояние между этими прямыми и радиус сферы, проходящей через точки A, B, E, F.

Ответ:

опущенная на основание, равна . На ребрах SA и SD

расположены точки E и F так, что AE = 2ES, SF = 5DF. Через точки E и F проведена плоскость α, параллельная CD. Найти
площадь фигуры, полученной при пересечении пирамиды плоскостью α;
радиус сферы с центром в точке A, касающейся плоскости α;
угол между плоскостью α и плоскостью ABC.

Ответ:

- середина ребра AC. Найти: а) расстояние от точки M

до плоскости SBC; наибольшее возможное значение угла между прямой SM и плоскостью SBC.

Ответ:

в грань ABC. Окружность верхнего основания цилиндра пересекает ребра DA,

DB и DC, а ее центр лежит на грани ABD. Радиус цилиндра равен 3 объем пирамиды ABCD равен , ребро . Найти двугранный угол между гранями ABC и ABD и радиус описанной около ABCD сферы.

Ответ:

основания конуса в точках A и B. Медианы AC и

SB треугольника ASB имеют длину m1 и m2 соответственно. Определить величину угла при вершине S в осевом сечении конуса, если известно, что площадь ∆ASB имеет наибольшее возможное значение.

Ответ:

нижнее основание призмы лежит в плоскости основания конуса, а вершины

верхнего основания лежат на боковой поверхности конуса. Известно, что площадь полной поверхности этой призмы имеет наибольшее возможное значение. Найдите объем призмы, если известно, что длина образующей конуса равна , а угол при вершине осевого сечения конуса равен α.

Ответ: при

при

равен R. Прямая, проведенная в плоскости основания конуса, пересекает диаметр

AC окружности основания под углом , а окружность – в точках B и D. Определить объем пирамиды PABCD, если известно, что угол в осевом сечении конуса при вершине P равен α, а треугольники APC и DPB равновелики.

CD = α и AD = BC = b
r –

радиус основания, тогда

радиус основания конуса
^APP1 =
^APP1 =
r = Rsinα
,
б)

т.е. в этом случае