СЕЧЕНИЕ ЦИЛИНДРА ПЛОСКОСТЬЮ. ЭЛИПС.

№ 54 имени П.М. ВОСТРУХИНА
Презентация
СЕЧЕНИЕ ЦИЛИНДРА ПЛОСКОСТЬЮ. ЭЛИПС.
Выполнил:
Студент группы 12РТООР1
Лядник

Алексей

Руководитель:
Преподаватель математики Т.Н. Рудзина

Москва.
2016г.

некоторой плокости α, и некоторую прямую S, пересекающую эту плоскость.

Через все точки данной линии l проведем прямые, параллельные прямой S; образованная этими прямыми поверхность α называется цилиндрической поверхностью. Линия l называется направляющей этой поверхности, прямые s1, s2, s3,... − ее образующими.

а с торцов двумя плоскими параллельными основаниями. Оба основания цилиндра

равны, также равны между собой и все образующие цилиндра, т.е. отрезки образующих цилиндрической поверхности между плоскостями оснований. Цилиндром (точнее, круговым цилиндром) называется  геометрическое тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов (рис. 1).

кругов, − образующими цилиндра. Так как параллельный перенос есть движение,

то основания цилиндра равны. Так как при параллельном переносе плоскость переходит в параллельную плоскость (или в себя), то у цилиндра основания лежат в параллельных плоскостях. Так как при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние, то у цилиндра образующие параллельны и равны. Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих. Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований. Прямой цилиндр наглядно можно представить себе как геометрическое тело, которое описывает прямоугольник при вращении его около стороны как оси (рис. 2).

3, а). Две его стороны − образующие цилиндра, а две

другие − параллельные хорды оснований. а)                б)     в)                   г) 
Рис. 3 – Сечения цилиндра
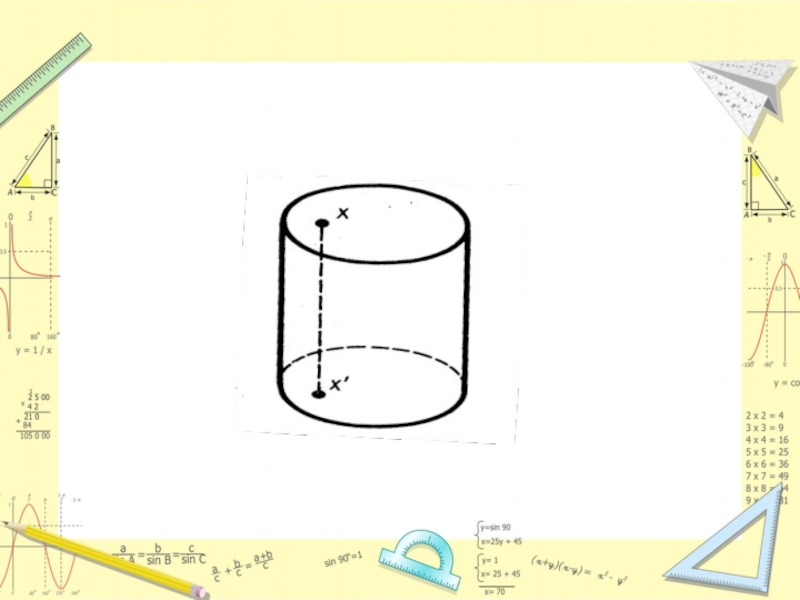
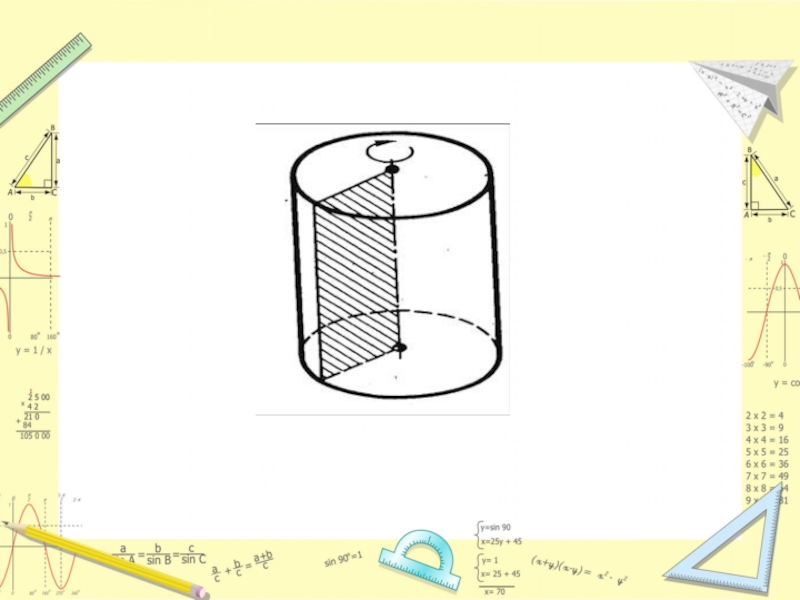
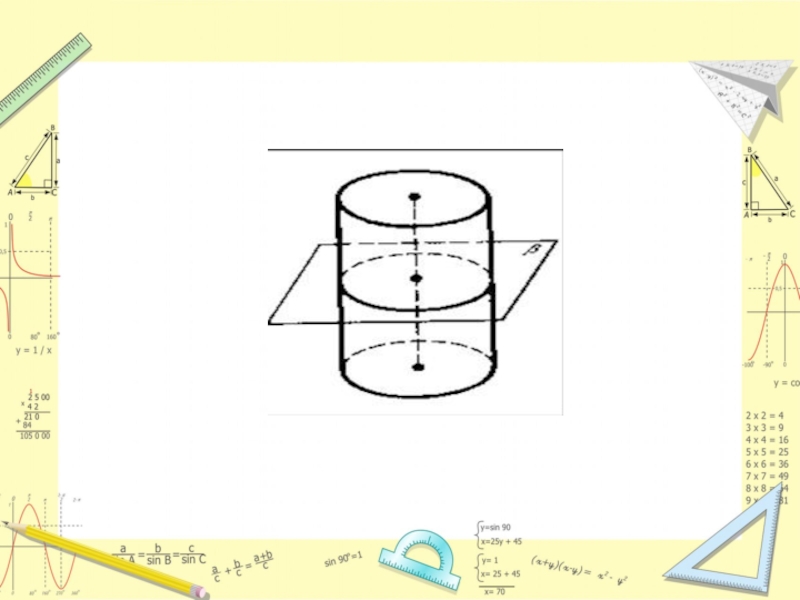
В частности, прямоугольником является осевое сечение. Это − сечение  цилиндра плоскостью, проходящей через его ось  Сечение цилиндра плоскостью, параллельной основанию – круг. Сечение цилиндра плоскостью не параллельной основанию и его оси – овал.
Теорема 1. Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.

Доказательство. Пусть β − плоскость, параллельная плоскости основания цилиндра. Параллельный перенос в направлении оси цилиндра, совмещающий плоскость β с плоскостью основания цилиндра, совмещает сечение боковой поверхности плоскостью β с окружностью основания. Теорема доказана.  

двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая,

чем расстояние между фокусами. Постоянную сумму расстояний произвольной точки эллипса до фокусов принято обозначать через 2а.

Нам дан эллипс. Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данного эллипса располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение данного эллипса имеет вид

выборе системы координат оси координат являются осями симметрии эллипса, а

начало координат - его центром симметрии (рис.). Оси симметрии эллипса называются просто его осями, центр симметрии - просто центром. Точки, в которых эллипс пересекает свои оси, называются его вершинами. На рис. Вершины эллипса суть точки A’, A, B’, B. Часто осями эллипса называются также отрезки A’A=2a и B’B=2b; вместе с тем отрезок ОА=а называют большой полуосью эллипса, отрезок OB=b - малой полуосью.