Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Золотое сечение (11 класс)
Содержание
- 1. Золотое сечение (11 класс)
- 2. Содержание Понятие золотого сечения ‘’Золотой’’ треугольник ‘’Золотой’’
- 3. Золотое сечение – это деление отрезка, при
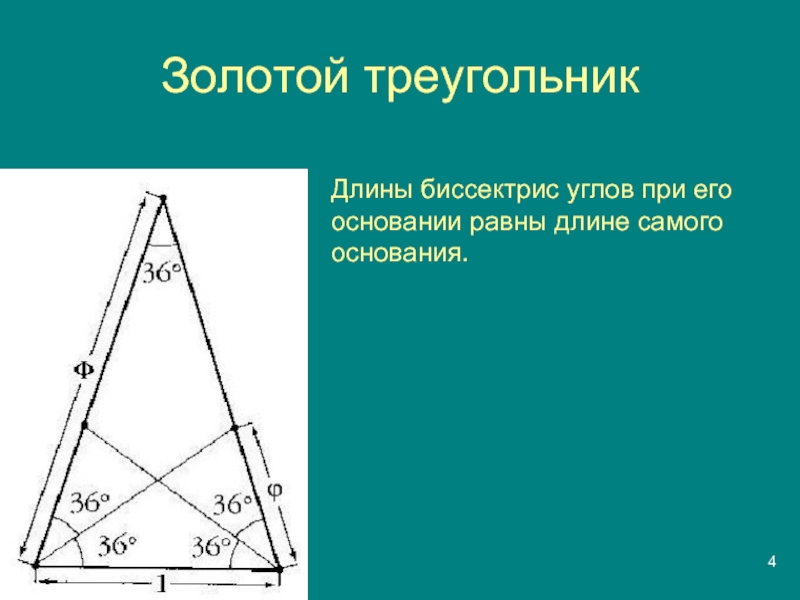
- 4. Золотой треугольникДлины биссектрис углов при его основании равны длине самого основания.
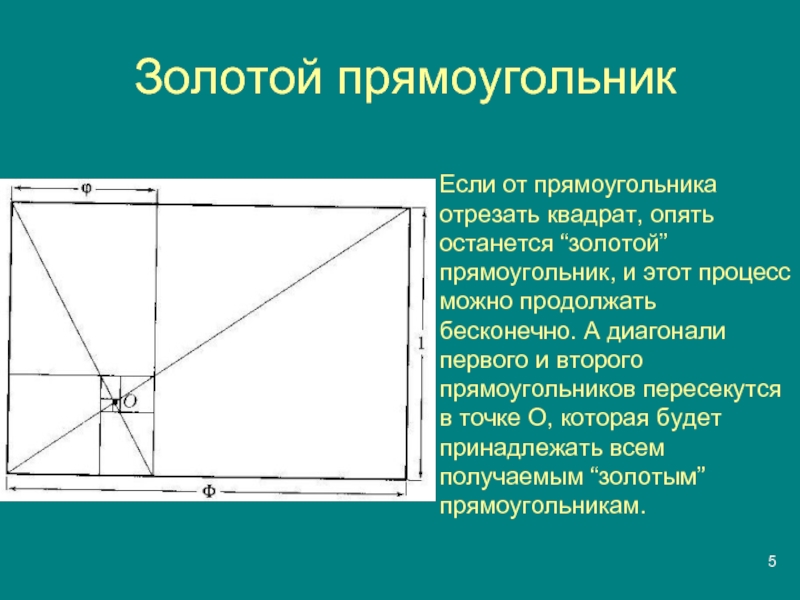
- 5. Золотой прямоугольникЕсли от прямоугольника отрезать квадрат, опять
- 6. Золотое сечение отрезка АВЗолотое сечение отрезка АВ, выполненное с помощью циркуля и линейки.
- 7. Пятиконечная звездаКаждый конец пятиугольной звезды представляет собой
- 8. Золотое сечение в ботаникеРассматривая расположение листьев на
- 9. Золотое сечение в искусствеПортрет Монны Лизы (Джоконды)
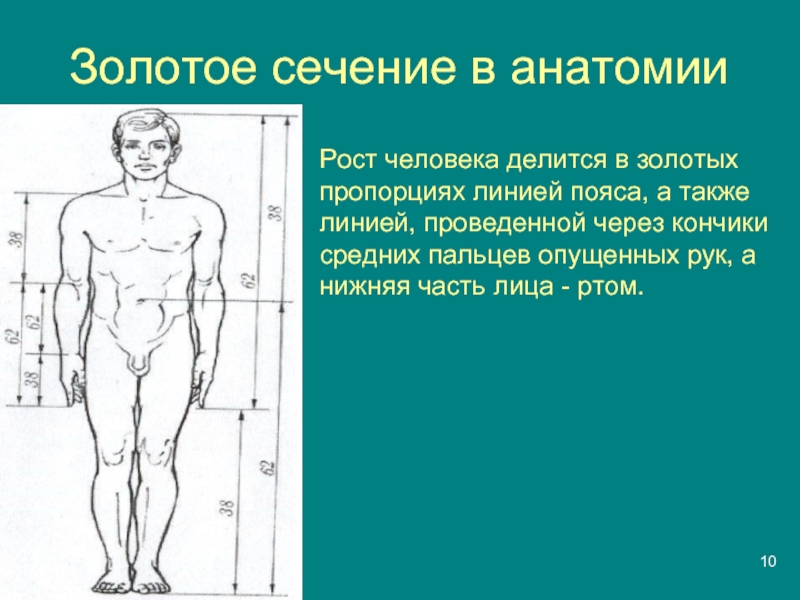
- 10. Золотое сечение в анатомииРост человека делится в
- 11. Золотое сечение в скульптуреЗолотая пропорция статуи Аполлона: рост изображенного человека делится пупочной линией в золотом сечении.
- 12. Золотое сечение в древней архитектуре12Парфенон имеет 8
- 13. Золотое сечение в современной архитектуреПропорции
- 14. Золотая пропорция встречается в конфигурации растений
- 15. Скачать презентанцию
Содержание Понятие золотого сечения ‘’Золотой’’ треугольник ‘’Золотой’’ прямоугольник Золотое сечение отрезка Пятиконечная звезда - пентаграммаЗолотое сечение в ботаникеЗолотое сечение в искусствеЗолотое сечение в анатомииЗолотое сечение в скульптуреЗолотое сечение в современной архитектуреЗолотое
Слайды и текст этой презентации
Слайд 12008
МОУ СОШ №80 г. Владивостока
ЗОЛОТОЕ СЕЧЕНИЕ
Разработал:
ученик 11А класса
Королёв А.А.
Руководитель:
учитель математики
Слайд 2Содержание
Понятие золотого сечения
‘’Золотой’’ треугольник
‘’Золотой’’ прямоугольник
Золотое сечение
отрезка
Пятиконечная звезда - пентаграмма
Золотое сечение в ботанике
Золотое сечение в
искусствеЗолотое сечение в анатомии
Золотое сечение в скульптуре
Золотое сечение в современной архитектуре
Золотое сечение в древней архитектуре
Заключение
Слайд 3Золотое сечение – это деление отрезка, при котором длина всего
отрезка так относится к длине его большей части, как длина
большей части к меньшей, это соотношение приблизительно равно 0,618.Слайд 5Золотой прямоугольник
Если от прямоугольника отрезать квадрат, опять останется “золотой” прямоугольник,
и этот процесс можно продолжать бесконечно. А диагонали первого и
второго прямоугольников пересекутся в точке О, которая будет принадлежать всем получаемым “золотым” прямоугольникам.Слайд 6Золотое сечение отрезка АВ
Золотое сечение отрезка АВ, выполненное с помощью
циркуля и линейки.
Слайд 7Пятиконечная звезда
Каждый конец пятиугольной звезды представляет собой “золотой” треугольник. Его
стороны образуют угол 36° при вершине, а основание, отложенное на
боковую сторону, делит её в пропорции золотого сечения.Слайд 8Золотое сечение в ботанике
Рассматривая расположение листьев на стебле растений, можно
заметить, что между каждыми двумя парами листьев третья расположена в
месте золотого сечения.Слайд 9Золотое сечение в искусстве
Портрет Монны Лизы (Джоконды) основан на “золотых”
треугольниках, являющихся частями правильного звёздчатого пятиугольника.
Слайд 10Золотое сечение в анатомии
Рост человека делится в золотых пропорциях линией
пояса, а также линией, проведенной через кончики средних пальцев опущенных
рук, а нижняя часть лица - ртом.Слайд 11Золотое сечение в скульптуре
Золотая пропорция статуи Аполлона: рост изображенного человека
делится пупочной линией в золотом сечении.
Слайд 12Золотое сечение в древней архитектуре
12
Парфенон имеет 8 колонн по коротким
сторонам и 17 по длинным. Отношение высоты здания к его
длине равно 0,618. Если произвести деление Парфенона по золотому сечению, то получим те или иные выступы фасада.Слайд 13 Золотое сечение в современной архитектуре
Пропорции Покровского собора на
Красной площади в Москве определяются восемью членами ряда золотого сечения.
Многие члены этого ряда повторяются в затейливых элементах храма многократно.Слайд 14 Золотая пропорция встречается в конфигурации растений и минералов, строении
частей Вселенной, музыкальном звукоряде. Она отражает глобальные принципы природы, проникая
во все уровни организации живых и неживых объектов. Её используют в архитектуре, скульптуре, живописи, науки, вычислительной технике, при проектировании предметов быта.Творения, несущие в себе конфигурацию золотого сечения, представляются соразмерными и согласованными, всегда приятны взгляду.
Золотое сечение лежит в основе гармонии и красоты мироздания.
14
Заключение
Теги