Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1Наука. В философии наука рассм-ся как одна из форм обществ-го c ознания
Содержание
- 1. 1Наука. В философии наука рассм-ся как одна из форм обществ-го c ознания
- 2. 2 .Предмет мат-ки://классич и совр предст-ия. Во
- 3. 2)в мат.изуч.не только понятия,возникш.при рассм.реальн.объектов,но и св-ва
- 4. 3. Мат. мод-ие. Мат модель - приближённое
- 5. 4.Абстрагирование в мат-ке. В самом широком смысле
- 6. примитивная чувственная абстракция — отвлекается от одних
- 7. 5.Акс. метод. Общ. хар-ка.(неопр.понят-отнош-акс-теор-новые понятия) основоп.метода- Аристотель,Платон.Осн.идеи:1)все
- 8. 3)(теоретическая) аксиомы,правила вывода(дедукция). Гильберт в 20х гг
- 9. 6. Мат-ка в XVIII в. Январь 1724
- 10. 7.Мат-ка в России в пер. пол. Х1Хв.
- 11. 8.Мат-ка в России во втор.пол. XIX -
- 12. . Непосред. ученики - Коркин, Марков, Ляпунов,
- 13. 9. Стан, сов.мат.шк. Виноградов(Петерб-Пермь),Лузин, Хинчин (Иван-Вознесенское мат.об-во1920).Москва-Егоров,приезды
- 14. дифф.ур-я. 1927 - Всерос.мат.съезд в Ленинграде, 1930(Харьков)
- 15. 10.Сов.мат.шк. - одна из ведущих маг. шк.мира
- 16. 2)После 2 мировой войны интересы мат-ки стали
- 17. 11.МО в России в пер. пол. XVIII
- 18. Рез-т обуч-я в гимн-огромный отсев.
- 19. 12.МО во втор. пол. XVIII. 25 янв
- 20. • вышний кл: продолжение изуч-я арифметики, алг
- 21. 13. ОМО в пер. пол. XIX в.
- 22. 1)жесткой сословностью, 2)ограничением ун-тской автономии, ослаблением влияния
- 23. 14.МО в росс-ой ср.шк. втор. пол. XIX
- 24. Матем содержаниеее хар-сь след. особен-ми:1) сущ-ем элем.и
- 25. 15. Реформы МО втор.пол.ХХв. 1964 учреждена комиссия
- 26. 1978 г.-10 летие программ, критика: статьи Понтрягина.
- 27. 1Г. Элементы топологии графов. Применение теории графов:
- 28. Теорема Клячко: независимо от нач. распол-ия автомобилей
- 29. Контуром в графе наз-ся замкнутая цепочка ребер,
- 30. 2Г. Эл-ты фракт. геом. Пон.«фрактал» и «фракт.геом.»
- 31. Алг.фракталы. Метод построения алг.фракталов:1.Выбирается фор-ла, в нее
- 32. ЗГ. Фракт.разм-сть.опр. фрактал-мн-во с дробной размерностью.опр.(мандельброт)фракт-мн-во,размерн. Хаусдорфа-Безиковича кот-го
- 33. 4Г. Эл-ты теории узлов. Под УЗЛОМ поним-ся
- 34. 1. Идея алгоритма Рейдемейстера: сведение сложной простр-ной
- 35. 5Г. Проблема сравнения узлов. Проблема сравнения: найти
- 36. Арифметика узлов. Произведение (композиция) узлов A и
- 37. 6Г. Элементы теории кос. Мат. коса состоит
- 38. Теорема о косах: Умножение кос обладает след,
- 39. 7Г. Прямолинейные и криволинейные симплексы. Гомотопия -
- 40. Понятие n-мерного симплекса. Барицентрические координаты. Пусть Ао,
- 41. Криволинейный симплексы образуют конечное симплициальное разбиение
- 42. Слайд 42
- 43. 20. Алгебраические числа. def: Комплексное число называется
- 44. Теорема 1. Минимальный многочлен рα является неприводимым
- 45. 21.Квадратичные вычеты и невычеты. Рассмотрим двучленные сравнения
- 46. Доказательство. Докажем сначала, что а непременно удовлетворяет
- 47. Но по теореме Ферма-Эйлера
- 48. 22. Мультипликативные функции Def. Функция θ: R
- 49. Лемма 1. Пусть
- 50. Пример 2. Сумма делителей данного числа. Пример
- 51. 23 Понятие поля. Def. Полем называется коммутативное
- 52. Пусть
- 53. Пр1. Поле рацион. чисел является подполем поля
- 54. Если размерность этого векторного пространства конечна, то
- 55. 25. Билинейные формы. 1. Билинейные формы. Пусть
- 56. Матрица билинейной формы. Пусть L – линейное
- 57. Ранг билинейной формы. Невырожденные формы. Из формулы
- 58. Слайд 58
- 59. Слайд 59
- 60. 12. Алгебра Ли над полем. Опр. Векторное
- 61. Пр2. Любое ассоциативное кольцо можно сделать алгеброй
- 62. Алгебры Bl и Dl – алгебры ортогональных
- 63. Слайд 63
- 64. Скачать презентанцию
2 .Предмет мат-ки://классич и совр предст-ия. Во 2 пол 19в ФридрихЭнгельс дал классич.опр. предмета-мат-ка имеет своим объектом простр.формы и колич.отн.действит. мира, стало быть весьма реальный м-л. Следств.опр. Энгельса: 1)исходн.понятия матем., бывшие
Слайды и текст этой презентации
Слайд 22 .Предмет мат-ки://классич и совр предст-ия. Во 2 пол 19в
ФридрихЭнгельс дал классич.опр. предмета-мат-ка имеет своим объектом простр.формы и колич.отн.действит.
мира, стало быть весьма реальный м-л. Следств.опр. Энгельса: 1)исходн.понятия матем., бывшие предметом изуч.с самого заррожд.мат.науки,- нат.число,величина, геом.фигура-заимств.из реальн.мира. 2)специфика мат.сост.в том,что она выделяет кол.отн. и простр.формы, ,присущ.всем предм. и явл., не завис.от их веществ.содерж. Совр.предст.опредм.мат:Бурбрбакистская т.зрен.на предм.мат.нашла отраж.в раб.акад. Колмогорова и хар-ся след.2-мя тезисами:А) В основе всей матем лежит чистая теория множеств. Б) Спец-ые разделы матем занимаются структурами, принад-им тем или иным спец-ым родам структур. Каждый род структур опред-ся соотв-ей системой аксиом. Выводы: 1)В предм.мат.вход.формы и отн.реальн.мира,кот.облад. такой степенью независ.от содержан,что могут быть от него полностью отвлечены и отражены в понятиях с такой ясностью и точностью, чтоб дать основан. для чисто логич.разв.теории.Слайд 32)в мат.изуч.не только понятия,возникш.при рассм.реальн.объектов,но и св-ва «мыслим.объектов». 3) предмет
мат.нельзя подменить формальными логич.схемами.4)для совр.мат.хар-рен общий подход к предм.исслед.Она абстраг-ся
от конкр.прир.объектов и от конкр.содерж.отношений между ними.5) расшир.предм.мат.привело к сущ.расшир.самого понятия кол.отнош.и простр.форм Характерные черты: 1.Мат-ка изуч-т абстраг. св-ва предметов(число), она абсолютизирует свои абстракции.2.осн.м-д получения рез-тов - логич.вывод.,не опир.на эксперим.проверку.З.неприложимость мат.выводов.Если приняты исх.посылки,то получ.из них мат.путем рез-ты неприлож. 4.абстр-ции в мат-ке разв-ся ступенчато-от абстр.обобщ.св-ва реальн.предметов,к абстр.выс.уровня,как тополог.пр-во,алгоритм.5.св-во универс.прим-ти.Слайд 43. Мат. мод-ие. Мат модель - приближённое описание какого-либо класса
явлений, выраженное с пом. мат. символики. Процесс мат моделирования -
изучение явления с пом мат модели. Этапы мат моделирования: 1.Постановка з-чи(фор-ся цель иссл-я,качеств.описание объекта и его схематизация,задание точности расчета выбран.переменных).2.Мат.формулировка з-чи(запись ур-й, нер-в для каждого блока мат.модели,а также соотнош.выр-х связи между блоками). 3.Разработка алгоритма числен.реш.з-чи(примен.цифров.вычисл. техники для реализации мат.модели). 4.Реализация алгоритма в виде комп.программы.5.Проверка адекватности модели(треб.точность)6.Исслед-е мат.модели(вычислит.эксперимент и интерпретация получ.данных). Роль мат. моделирования в совр.науке и шк.мат.обр-ии. В совр.науке очень часто под мат. модел-ем стали понимать создание и изучение мат.моделей с пом ЭВМ. Пример - эколого-м-кая модель Азовского моря (расчёт разл.вариантов жизни Азовского моря: опр-е предельно допустимого уровня загрязнённости, засоленности ит.д.). Понятие мат.модели кладется в основу совр.шк.курсов явным образом. Так построены учебник алгебры и начал анализа А.Г. Мордковича. Осн.задача шк.курса мат.обр-ия - ознакомление уч-ся с соотн-ми реального и проектируемого мира и его мат.моделями. Ведущая идея курса - ф-ции, т.к. мат.модели напрямую связаны с ф-циями. Каждый год обучающийся ориентирован на конкретную модель реальной действит- сти.Напр,7 кл - равномерные процессы;8кл - равноускор.процессы;9 кл - периодические процессы; 1 Окл - процессы ограниченного роста.Слайд 54.Абстрагирование в мат-ке. В самом широком смысле слово абстракция означает
возм-сть рассмотр-ия предм-в и проц-в с к-л одной точки зрения
и отвлечения от др. сторон, моментов и обстоятельств. Типы (виды) абстракций: абст-ия отождествления, когда у предметов некот-го класса выделяется общее св-во, а от всех др. св-в отвлекаются.. Абстракция потенциальной осуществимости: отвлекаются от реальной возможности построения тех или иных мат.объектов и допускают осуществимость построения след.объекта при наличии достаточного времени, простр-ва и материалов. Например, вслед за данным нат.числом N допускается возможность построения след, за ним нат.числа N + 1; абстракция потенциальной бесконечности: потенциальная возможность построения в неогр-ом ряду след.объекта, если задан предыд.объект. абстракция актуальной бесконечности: отвлекаются от реальной возможности построения любого нат.числа и допускают возможность построения неогр-го мн-ва таких чисел, как актуально построенного, завершенного. Тем самым бесконечное мн-во уподобляется конечному мн-ву;Слайд 6примитивная чувственная абстракция — отвлекается от одних св-в предмета или
явления, выделяя другие его св-ва или качества (выделение формы предмета,
отвлекшись от его цвета или наоборот); обобщающая абстракция — даёт обобщённую картину явления, отвлечённую от частных отклонений. В рез-те такой абстракции выделяется общее св-во исследуемых объектов или явл-ий; идеализация — замещение реального эмпирического явления идеализированной схемой, отвлечённой от реальных недостатков. В рез-те образуются понятия идеализированных (идеальных) объектов «точка», «прямая»; изолирующая абстракция — тесным образом связана с непроизвольным вниманием, поскольку при этом выделяется то содержание, на котором сосредоточивается вниманием; конструктивизация — отвлечение от неопределённое границ реальных объектов, их «огрубление».Слайд 75.Акс. метод. Общ. хар-ка.(неопр.понят-отнош-акс-теор-новые понятия) основоп.метода- Аристотель,Платон.Осн.идеи:1)все предл.дел.на первон.(недоказ)предл.и кот.треб.док-
ва; 2)понят. кот.встреч.в предл.дел.на основн.(неопред)и кот.треб.определ.; 3)первонач.понят.не док-ся,т.к их истин.предполаг.
самоочевид. Содержательная акс. теория. наиб, известность этот м/д получил через «Начала» Евклида.Ак-ка Евкл.носит конкр. содержат.хар-р поскольку его понятия предполаг.единств. интерпрет., идеализир.интуит.предст.об окр.пр-ве. Т.о описывает конкретную структуру, используемая логика неопределяется. Полуформальная акс теория. Гильберт(1899)несвяз.с основн. понят.и акс.геом.к-либо конкр.истолкование. Аксиомы абстраг.от пространств.содерж.и могут описывать св-ва непространств. предм.ПАТ описывает род стр-р.исп.логика не опр-ся. ФАТ. описывает род стр-р, формализуются док-ва. ФАТ состоит из: 1)символы, знаки, к-рые обозначают объекты, операции, с пом. к- рых конструир-ся нов.объекты,правила образ-я 2)операции над символами, правила образ-я элемент.предл-й, оп.над элементарн. предл-ми, правила обр-я сложн.высказываний.Слайд 83)(теоретическая) аксиомы,правила вывода(дедукция). Гильберт в 20х гг XX в. предложил
т.н. «программа Гильберта». Её суть: для док-ва непротиворечивости м-ких теорий
он предложил строить их в виде ФОР-Х АКС-КИХ ТЕОРИИ, в к-рых само понятие «док-во» явл-ся точным, изучаемым спец дисциплиной - теорией док-ва. Курт Гёдель-автор фундам.откр.огр-ти акс.метода, и раб.в направл.мат.логики таких как теория. 1930-теорема о полноте исчисл.классич.логики предикатов. 1931-две теоремы о неполноте.Вывод:люб.процедура док-ва истин.утв.элемент.теории чисел заведома неполна. Из ФАТ родилась совр.мат дисциплина - «теория знаков».Слайд 96. Мат-ка в XVIII в. Январь 1724 - указ об
учреждении С.-ПбАН. Август 1725 - 1ые собрания в АН. Отличия
от Европ.АН:1.3 кл: мат, физ, гуманит-ый. Матем.кафедры: 1)матем 2)астрономии, геогр-ии и навигации 3)2механики; 2.АН должна была выполнять не только исслед-кие, но и учебные ф-ии. При ней созданы гимназия и ун-т.3.светск0сть:(3фак-та: филос,юрид,мед)АН нет каф.богословия.4.Гос.финанс-е(обсерватория, мастерские, лаборатории, библиотека, музеи, ботанический сад, издательство).Научная периодика:«КомментарииС-ПбАН», получ.европейск.признан.и популяр-ть. Научные и препод кадры 1725-27гг.-Решено произвести набор за границей. 17 професс. из них 7 матем (Швейцария, Германия). Герман, Н и Д.Бернулли, Голъдбах.(занимался более 30лет): ТЧ, ДифУр, теория рядов, геом. Роль Эйлера(1707-83) в становлении отеч матем. выходец из шк.Бернули,в Базеле не нашел примен.талантам. В 1727 приезжаете Питер. 41уехал,66приехал.Он заним. подгот. первых акад-в - матем. Рум.и Кот. Х-ка основных матем. достижений.Опубл. более 500книг и статей; оставил огромный архив, в том числе переписку сучеными.С 1911 г Швейцарским об-вом естествоиспытателей издается полное собрание сочинений - 72тома.Слайд 107.Мат-ка в России в пер. пол. Х1Хв. (Ал-др1)Образ.реф. Сперан: организ.6округов,в
центрах созд. ун-тов.В это врем функ-ли 3 ун-та:Моск.,Дерпский,Виленский (юридич, мед,
филос.).1804 г.-Казань, Харьков; 1819 - Петербург, 1835 - Киев. 1804 г. - нов. устав ун-та, по которому открытие физ-мат фак-тов.Харьковский ун-т:рек. Осиповский. Выдающ. вып-к семинарии, поставил препод. м-ки на мир.уровень. Выд. вып.Острогр.(не зак.курс). Казанский ун-т: Румовский(основ-ль). Карташевский (МУ), Бартельс - уч-ль Гаусса и Лобачевского - блестящий европ. учёный; Лобачевский - самый выд. выпускник ун-та, затем преподавал там Лобач. (1792-1856) Ректор Казанского ун-та, -создатель неевкл.геом., имеются раб.по теории сх-ти бескон. рядов, 1816-17 г.-читал лекции по геом., пытался д-ть 5 пост. 1826 г. - делает доклад отделению физ-мат наук Казанского ун-та. М.В.Остроград(1801-62) рус. м-к и механик, педагог, мат-к- методист.1817-1820 гг. - Харьковский ун-т. 1822 -1828 - Сорбонна, политехническая шк.,лекции Коши,Лапласа, Фурье, Лежандра. 1828 г. — Петербург, СПбАн: адъюнкт, 1830 г. - академик по прикладной м-ке. Работы по мат.физ. и мех-ке.М-ка: вариац. исчисл.,теория алгебр, ф-ий, ТЧ, алгебра, геом, т.в.. Особенно велико значение интегральных теорем Остроградского.Слайд 118.Мат-ка в России во втор.пол. XIX - нач.ХХв. Во 2пол19
в.-н.20в. матем преимущ-нно развивалась в ун-тах,сеть кот. расширилась. Физ-матем факультеты
открылись в: - Новороссийском ун-те,- Варшавский, - Северо-Кавказский .В 70е -практ.занят, фак-вы,кружки.2.Болыпую роль стали играть матем общества: Московское (1864)-стар. в мире, иниц-ры Брашман, Давидов; Харьк., Казан.; Петерб.3Возрастает роль науч съездов - 1 Всеросс.съезд естествоиспыт.и врачей (1868, Петерб): секция матем 6 докладов.4.Матем печать: «Матем сборник».Новый вид научн.периодики-реферат.журнал. без господдержки, на средства мат.обществ.5.Междунар. мат.конгрессы. 1-й Цюрих, 1897; 1900 Париж (23 пробл.Гильб). Некоторые не реш.до сих пор. П.Л.Чебышев (1821-1894). Рус мат.и мех., основоп. Петерб. мат.шк, ак-к СПбАН, 1837-41-учеба в моск.универ.1847-пригласили в Петерб.универ,1852 - появляется его работа о простых числах. Научные интересы:ТеорВер, т.ч., интегр. исчисл и др. 2пол19-нач20в х-ся возникн.1-х научных коллективов, самый первый из них Петерб. мат.шк Чебышева, (Эйлер и Острогр подгот почву дляее разв), к- рый возглавлял ее более ЗОлетСлайд 12. Непосред. ученики - Коркин, Марков, Ляпунов, Вороной. 1910г. Петерб.мат.шк
дала свои ответвл.в провинции: Бернштейн (Харьков), Граве, Крылов(Киев), Чеботарев (Казань),Мордухай
- Болтовской (Ростов). Моск.мат.шк. В Мск первоклассные мат-ки появляются только к 1910г. В это время заложены основы моск.мат.шк, к-ая первонач. была шк (ТФДП). Дм.Фед.Егоров- Рус.совет.мат, президент моск.мат.общ., один из основателей моск.мат.шк.Ученики Егорова-Лузин, Степанов, Петровский, Привалов, Фиников.Ник.Ник.Лузин (1883-1950) Сов.матем, ак-к АН СССР. Создатель советской шк. метрической ТФДП. 1910-1914: направлен в Геттинген и Париж (Пуанкаре, Адамар, Дарбу, Борель, Лебег). 1912 Доклады Парижской АН, 1914-МУ, фак-в по ТФДП. Ученики: Келдыш,Урысон, Люстерник, Новиков, Александров. Отношение между Петербургской (классика) и Московской (современность) научными шк не сложились с самого начала. Петер. - классич. проблемы матем-ки, а Моск-ая - самые современные.Слайд 139. Стан, сов.мат.шк. Виноградов(Петерб-Пермь),Лузин, Хинчин (Иван-Вознесенское мат.об-во1920).Москва-Егоров,приезды Лузина.Несм.на трудн-ти мат.продолж.
разв.и в годы рев-ции и гражд.войны,т.к.для ее разв.не нужны большие
матер.вложения. 1918- декрет об орган.первого НИИ-ЦАГИ-директор Жуковский. 1921 - по инициативе Стеклова организован физ-м-кий ин-т АН (Петроград). Преимущества НИИ: - развитие науч. Исслед-й орг-ции конференций, -редактирование науч.исслед-ий.ВОЗРОЖД.М-КИХ ИССЛЕД.1922 - в Москву вернулся Лузин, возобн. засед. семинара, расшир. тематики: -ТФКП (Лузин, Привалов, Хинчин, позже - Лаврентьев, еще позже - Келдыш); - топологияУрысон, Александров, позже - его ученики: Тихонов, Понтрягин);-тео.вер (Хинчин, Колмогоров); -проблемы мат логики (Колмогоров, позже - П.С. Новиков); алгебра (Шмидт, Курош). Благодаря школе Егорова и Лузина в нач ЗОх гг Москва - один из ведущих м-ких центров мира. В Ленингр.м-ки Стеклов,Делоне,Виногр. Осн.роль стал играть физ-мат. ин-т под рук-вом Стеклова. Направления исследований, в основном, классич-ие: мат.физика, ТЧ,Слайд 14дифф.ур-я. 1927 - Всерос.мат.съезд в Ленинграде, 1930(Харьков) Всесоюз.съезд м-ков: возобн.науч.периодика.
1934 - превод в Москву АН СССР и ряда ведущих
НИИ, в т.ч. «мат.ин-та им.Стеклова», -переезд в Москву Виноградова, Делоне, Соболева. В рез-те, две ведущие науч-е школы - Моск-я и Пет-ая (Ленинградская) - слились, став ядром сов-ой мат.школы.Слайд 1510.Сов.мат.шк. - одна из ведущих маг. шк.мира в XX в.
Сов.мат.шк достаточно сложное обр-ие, в свою очередь, состоящая из различных
школ и направлений, выросших из единого корня и объединенных общей историей. Она обладает рядом специф-их черт 1.появилась в ЗОе годы 20в, заявила о себе во 2 его половине.2.На протяжении многих послед-их лет ее развитие проходило в изоляции от зарубежных мат.центров.3.ее внутр-ий потенциал оказался настолько велик, что и в условиях замкнутости она продолжала успешно развиваться.4.обширная геогр-ия Москва,Ленинград,Минск,Киев,Харьков, Новосибирск, Тбилиси)5.осн.центр- Москва; мат.сообщ-во объединилось вокруг мат.инст-та им. Стеклова, Моск-го мат.общ- ва и мехмата МГУ. 6.Мат-ку сов.шк. отличает широта охвата тематики, в одном ряду только с США.7. Создание крупных матем школ: - прежде всего в центрах союзных республик. 8. Основ.напр-ния исслед-ий совет.мат.шк: 1)До 2 мировой войны осн. напр- ями в мат-ке был анализ и его ответвления (ТФКП, ТФДП, ур-я мат.физики, теория вероятностей.,).Слайд 162)После 2 мировой войны интересы мат-ки стали смещаться в область
топологии, алг.геом. 9.Сов.мат.шк. участвовала в крупнейших проектах века:новейшие вооружения, в
том числе атомного, космической программы.10.триумфом сов.мат.шк. стал междунар конгресс мат-ков(1966) Москва. Самый представит.за весь 20 век. 11. Высочайшая конкурент-сть сов.мат.шк д-на тем фактом, что начиная с 90г20в бывшие сов.мат-ки заполнили научн заведения Запада (Европа).Премия Аб.2009- Мих.Громов(Фр);Премия инст.Клэя2010-Перельман;Филд.медаль2006-Перельман,0куньков(сша);2010-Смирнов(швейц).11ремия Крафурда08-
Концевич(фр),Сюняев(рф,фрг).
Слайд 1711.МО в России в пер. пол. XVIII в. 14(25)янв1701 указ
об откр. Руко-ли:формально:Голвин. фактически:Курбатов (впосл. иниц. созд.более мас.цифирн.шк.Уч-лям: Фарварсон-разр.сис.обуч, преп.мат.дисципл.,редак.перев.начал.1702
- приглашен Магницкий - один из образованнейших людей того вр. Учебники: 1703, Л.Ф. Магницкий «Арифметика, сиречь наука числительная» (1703)-ариф(десятич.сист.нумер., десят.дроби, эл-ты алг.и геом); Я.В. Брюс «Приемы циркуля и линейки» (2е изд - глава Петра 1 1)орг-ия обуч-я: 3 ступен и :1.русская шк(обуч-е грамоте); 2.цифирная шк(обучарифметике);3.высшие классы(геом, тригоном, геогр, навигация). Роль:-1-й центр пропаганды науки,в т.ч.матем.-1-е уч.завед.кот.готов.уч-лей матем. В нач. 18в были созданы мат-нав, инженер., артиллерий.шк. Академ-ая сист-гимназия и ун-т при Спб.Хар-р: подготовит д/академ-го ун-та. Программа обуч-я первоначально разраб. 1-м презид.АН Блюментростом.Мос-кое обр-е. курс м-ки вкл-л в себя арифм., геом. и тригоном. Учебн. м-ки: первонач. это были учебн. Хр.Вольфа. После исп-сь учебн.Эйлера, Крафта, позже - Румовского.Слайд 18 Рез-т обуч-я в гимн-огромный отсев. За первые «
30 лет ни один гимназист не стал студентом ун-та. При
Ломоносове - 24 гимназиста стали студентами. В 1805 закрыта. Роль Эйлера в становлении отеч-го м-кого обр-я. Эйлер (1707-1783).По прибытию в Россию (1727) ему сразу же поручили препод. м-ки в обоих учебных заведениях. Эйлер в 1737 сост-л проект программы гимназ-го курса.1языки: лат и нем,2.м-ка: арифм, геом, учение о шаре,3.каллиграфия, ист, география, рисование, танцы. Метод.шк.Эйлера:Курганов,Котельн,Рум,Голов,Фусс.Мет.идеи: 1.выделен.арифм,геом,триг,алгебры-классич.набора шк.дисципл;2.Сис-кое излож.мат-ла в учебн.; З.Разумн.сочит.теории и практ.; 4.Созд.руск.мат.терминолог.
Слайд 1912.МО во втор. пол. XVIII. 25 янв 1755г указом импер.Елиз.по
иниц.Ломоносова, поддерж.гр.Шувалова, учрежден МУ.Стру-ра МУ:Фак-ты: фил-ский (Зг), юридич и мед
(4г). М-ка-вспомог-ый предмет. 1758г появл-ся каф. м-ки. Чист.мат:арифм,алг, геом, тригон. Прикладн: оптика.мех.астном. .Препод.кадры. 1ым спец- ом-мат-ком в МУ был Аничков, ученик Барсова, к-рый принял от него каф чистой м-ки. Учебники м-ки. Первоначально в основу преподавания м-ки был положен учебник Вейдлера. созданные позже учебники Аничкова. Но уровень преподавания м-ки в МУ в 18 в. был невысоким. Осн.заслуга ун-та перед МО закл-сь в подготовке пед.кадров д/него самого, д/гимназий.Мат. обр-е в гимназиях и пансионах при МУ В 1755 г были созданы 2 гимназии: д/детей дворян и разночинцев. Стру-ра гимназии при МУ :Pvc. шк (нач-я): чтение, письмо,грамматика. После рус шк можно было пере-йти в лат шк (после нее можно поступить в ун-т) или в шк новых европейских языков (после нее поступить в ун-т нельзя).Матем.изуч.только в лат щк: • нижний кл: 4 действия арифметики (2ды в нед по 4 ч); • ср кл: м-ка: дроби, эл-ты геом, и алг (4ч в нед);Слайд 20• вышний кл: продолжение изуч-я арифметики, алг и геом (по
4 ч в нед).1779-при МУ создан Моск благородный ун-тский пансион.
По его образцу были созданы благородные пансионы (дворянские шк) в крупн. губерн. городах: Нижн Н, Тверь, Курск,...МУ курировал и их: в нем готовились прец,учебн,денежные средства. 1786 устав о нар.уч-щах.в уездн.городах-малые 2- хклассные нар.уч-ща,в губернских-главные нар.уч-ща(5лет). Развитию сети нар.уч-щ препятств.нехватка мат.средств и отнош. населения. Мат-ка один из осн.предм.изуч:в малых уч-щах-1кл.-уст.,письм.счет;2кл-арифм(до тройного правила),в главных-1 -2кл-тоже что и в малых,Зкл-дроби,в т.ч.десятичн.,4кл-осн.геом. Были созданы приходские, уездные, губернские уч-ща. Уч-ик мат-ки для нар.уч-щ: «рук-во к арифм»(1783)(автор не указ.), «краткое рук-во к гимназии»(1786)-Головин. Янкович де Мериев разработал методику изуч-ия мат-ки.Слайд 2113. ОМО в пер. пол. XIX в. Обр-е реформы нач
века. Александр 1 в нач царств.считал обр-е важн ресурсом реф-ния
страны. Сперанский-Цель обр-ных реформ: поощрение и даже принуждение чиновн. и дворян к получ. обр-я. 1802-созд.мин-ва нар. просв. 1-й министр-Заводовский. Стр-ра обр.сис.-учебные округа:Пб. Москов., Белорусско- Литовский, Казан., Харьк. В каждом округе ун-ты—>шк: приход-ская (1 г),уездная (2 г),гимн.(4 г). Фуркация обр-я: на нач-е (приходские уездные училища), ср (гимназии), высшее (ун-т). 1803 - необх-ть диплома гос или частного уч заведения д/ поступления на службу. 1809 - «указ об экзамене на чин». Устав ун-та в 1804 г- 4 фак-та: 1)нравств.и политич., 2)физ.и мат., 3)мед. наук, 4)словесных наук.Учебн. м-ки: Осиповского; Фусса- 1й стабильный учебник м-ки д/гимназий до 1828 г. Мин-во духовных дел и народ.просвещ.(Голицын)«Чистки»Казан.,Петерб.ун-тов,лишен должн. Осиповский.Гимназ.обр:-уменьш.финансир,-введ.закона божия,-усилен, классич.нач. МО в России в ЗОх - нач 50х гг XIX Уваров - министр нар просвещ-я (1833- 1849).Созданная им сист обр-я хар-сь:Слайд 221)жесткой сословностью, 2)ограничением ун-тской автономии, ослаблением влияния ун-тов на школу
(новый устав ун-тов 1835г), 3)жестко централизованной сис. управле-ния обр-ем, 4)усилением
классич. начала (изуч-е древних языков) в гимн.обр.Цель - уберечь Россию от революционных потрясений. Цирк-ное предлож. мин-ва от 15 дек 1845 «Об ограничении в гимназиях препод. м-ки» :1.отменялось преподавание аналит. и начерт.геом.2.предл. новое распред. уроков м-ки (объем и п-ть изуч-я м-ки по классам и м-ким дисциплинам). На основании этого Буссе составлен проект программы по м-ке (1846):1.усилена прикладная сторона арифм., алгебры, тригон.2. За счет искл-я начерт. и аналит. Геом расширен курс алгебры. 1848-М-ка усилена с 20 до 30 нед-х ч.Учебн.м-ки:Москва: Перевощикова (МУ);Казань: Лобачевского, Буняковского. Буссе сост. комплект - учебник, задачник, рук-во учителю.Слайд 2314.МО в росс-ой ср.шк. втор. пол. XIX в. Александр2.Ун-там: -
возвр. автономия; - право выписывать из-за границы науч и учебную
лит-ру без цензуры; - неогран, прием студентов; - присутствие на лекциях вольнослушателей, в том числе женщин. 1864 г. пед.съезд директоров и уч-лей (Одесса). На нем рассм. и проблемы связанные с обуч. матем: - содержание матем: была отмечена перегруж-ть программ 1852. В 1864 г. утв-н новый устав гимназий.В соотв., с кот.были опре-ны 3 типа гимназий (7 лет): * классич с 2др.языками (лат и греч); * классич с 1 др. языком; * реальная. Реформа МО в России в 70-х гг. XIX в.1866 Министром назн-ся гр.Толстой.Он боролся с просвещением бедных слоев населения. В 1871 г. утв. новый устав гимназий, просуществовал до 1917 г. В соответствии с ним все гимназии преобр.в классич с 2 др.языками. Матем: - приведена к минимуму; - усилен формализм в док-ти; - все прикладное искл. Объем часов(206ч):матем-28, лат-49, греч-З6.КСШМО и ее рос. Модель к 90-м гг. XIX в. уч. предмет «матем» стабилизировался, в результате чего сложилась КСШМО.Слайд 24Матем содержаниеее хар-сь след. особен-ми:1) сущ-ем элем.и высш. матем.2) разд.
элем.матем. на 4 уч.предмета - арифм, алг, геом и триг.З)
изуч. в высш шк - аналит геом и мат.ан.Недост:1) несоотв. м\у развив, наукой матем и предметом;2)разрыв между эл-ной и высш.мат.;3) отсутствие проп-го курса мат. В рез-те мат.: до 10 % уч-ов не переходила в след.класс. Классич комплект отеч учебников. Для нач.шк.Евтушевского и Гольденберга.Для ср.шк.По арифм.- книги Малинина и Киселева. По алг.и геом. Киселева; Рыбкина,по тригон.- Рыбкина. Движ. за реф. Нач. связ. с 1 междунар. мат. конгр.в Цюрихе в 1897 г. и с им.Ф.Клейна.«Меранская прогр»Клейна опублик. 1905г. Движ за реф в России. С 1891 в печати появл.критика.сис. МО. Конгресс принял решение о необходимости: - устан. внутрипредметных связей между арифм., алг., геом.и тригон.;- внедрения элементов высшей матем;- изменения содержания и методов решения задач.Слайд 2515. Реформы МО втор.пол.ХХв. 1964 учреждена комиссия по определению содержания
ШМО при АН. Возглавил комиссию Колмогоров - выдающийся отеч.ученый XX
в. Подготовка реформы: - создан проект программ, авторские коллективы для написания учебн-в, -проведен опережающий экспер-т; - В 1969/70 уч. году введены новые программы и учебн-и.Ситуация в шк: вводится всеобщее сред.обр-ие, борьба с неусп-стью и второгодничеством. Осн. пол-ия реформы: - нач.шк(1-3 кл):вместо арифм. матем-ка (ариф+пропед алг и геом); - ср.шк(4-10 кл):матем 4-5 арифметика + пропед.алг и геом на теоретико-мн-ной основе. Алгебра: в основе теоретико-мн-ные понятия ф-ии, ур- я. Геом: в основе геом преобр-я пл-ти и пр-ва, век-ное построение стереометрии. Введены эл-ты мат.ан. Вед.идеи - разв-е мышления, лог-й к-ры; сис-ма упр-й направлена на показ идейного богатства курса мат-ки. Учебн. матем: Матем 4-5 Виленкина и др. Остальные учебн-и созданы преимущественно людьми, не знающими школы.Учебн-и неудачны, особенно трудны учебн-и геом-ии.Слайд 261978 г.-10 летие программ, критика: статьи Понтрягина. 1981 г.-опубликованы «треб-я
к мат.подготовке уч-ся, вкл. содержание обучения мат-ке» - параллельно перерабатываются
«колмогоровские» учебники по алг и геом, проходит их экспериментальная проверка. контрреформация 1981:- Перерабатываются Колмог. учебники «матем 4-5 и алгебра 6-8» и появляются альтернативные; - Отказываются от учебников Колмогорова и др. (6-8), Скопеца и др. (9- 10). Вводятся учебники геометрии: 1) Погорелова и 2) Атанасяна и др.Слайд 271Г. Элементы топологии графов. Применение теории графов: электросхемы ,схемы трансп-ых
коммуникаций, геогр. карты, структурные формулы молекул, генеалог, экономика и статистика,
теория расписаний и дискретной оптимизации. Жордан Камиль Мари Эдмон -франц мат-ик. Осн. рез-т: т. Жордана о кривой - тополог-ий рез-т из комплексного анализа. Урысон сов.мат-к. , один из крупнейших спец-ов в обл-ти топологии, создавший новое напр-ие - теорию размерности. В 1921-22 в МУ он прочитал впервые в.России курс топологии. Александров изв- ый сов. мат-к, спец-т по топологии. Академик АН СССР. Вместе с Урысоном основал и развил теорию компактных и бикомпактных пространств. Ввёл ряд фунд-ых понятий и конструкций топологии. Создал теорию существенных отображений и гомологическую теорию размерности, приведшую к ряду основных законов двойственности, связывающих топологические св-ва фигур и мн-в с топол-ими св-ми доп. части пр-ва. Лемма Столлингса: если в некот. городе по каждой улице между 2 соседними перекрестками разрешается двигаться только в одном направлении, то обязательно найдется квартал, вокруг которого можно объехатьСлайд 28Теорема Клячко: независимо от нач. распол-ия автомобилей регулярное движение без
столкновений не может быть вечным, иначе говоря, по прошествию некотор.
времени неизбежно столкновение какой-то пары автомобилей Граф наз-ся уникурсалъным, если его можно «нарисовать одним росчерком», т.е. обойти его весь непрер-ым движением, не проходя одно и то же ребро дважды. Св-во графа быть уникурсальным явл-ся тополог-им. Выводы Эйлера: 1 .Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа всегда чётно. Невозможно начертить граф, к-ый имел бы нечётн. число нечётн. вершин.2.Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине-.3.Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком. Граф кёнигсбергских мостов имел четыре нечётные вершины, -следовательно невозможно пройти по всем мостам, не проходя ни по одному изних дважды.Слайд 29Контуром в графе наз-ся замкнутая цепочка ребер, объедин-е еоторых представляет
собой замкнутую линию. Связный граф не содержащий контуров – дерево.
Разность В - Р наз-ся эйлеровой характ-ой графа, где В – число вершин, Р — число ребер графа. Эйлерова хар-ка дерева равна 1. Граф, к-ый можно нарисовать так, чтобы его рёбра не пересекались (нигде, кроме вершин) называется плоским. Граф наз-ся вложимым в плоскость, если существует на пл-сти граф , гомеоморфный . Пример 1 . . Можно ли на пл-сти провести тропинки от каждого домика к каждому колодцу так, чтобы никакие 2 тропинки не пересеклись? Граф. не вложимый в плоскость. Обозначим его P1Пример 2. Полный граф с пятью вершинами, т.е.граф без петель, любая пара вершин которого соединена ребром. Теорема: Если некот-ый граф содержит подграф, гомеом- ый P1 и Р2, то граф не вложим в пл-сть. Опр. Гомеом- ый образ окр-сти наз-ся простой замкнутой кривой. Т. Жордана: Мн-во всех точек пл-сти, не лежащих на простой замкнутой кривой, разбивается на 2 области: внутр. и внешн.Слайд 302Г. Эл-ты фракт. геом. Пон.«фрактал» и «фракт.геом.» появ. в сер
70х гг 20в, а с сер 80х гг прочно вошли
в обиход мат-ков и программистов. Слово «фрактал» от лат.означ «сост. из фрагментов, дробный, ломаный».ОПР1.(данное Мандельбротом) ФР-ЛОМ н-ся стр-ра, сост. из частей, к-рые в каком-то смысле подобны целому (самоподобная структура). ОПР2.САМОПОД ГЕОМ ФИГУРОЙ (телом) н-ся фигура, к-рую можно разрезать на конечное число одинак фигур, подобных ей самой.Геом. фракталы: Триадная кривая Коха. Постр.: 1. Построение отрезка единичной длины - это нулевое поколение криво й Коха. 2. Далее каждое звено (в нулевом поколении 1 отрезок) замен на образующий эл-т. В 1-м пок-нии - это кривая из 4х прямолин звеньев, каждое длиной по 1/3. Кривая n-го поколения при любом конечном n н-ся предфракталом.При n стрем к бесконечностиух кривая Кох становится фрактальным объектом.Вычислим пл-дь салфетки Серпинского. Пусть S⌂=1 -площадь исходного треу-ка. 1й уровень: S1=l-l/4=3/4; 2й ур: S2=3/4-3/l6=9/16; S3=9/16-9/64=27/64; ...Выбрасывали: 1/4, 3/16, 9/64,...Найдем сумму беск.убыв.геом.прогрессии, составленной из площадей выбрасываемых тр-ков. b1=1/4, q=3/4, S = b1 / (1-q) = 1/4/ (1-1/3) = 1.Была S=l, выбросили S=l. получили площадь салфетки Серпинского =0Слайд 31Алг.фракталы. Метод построения алг.фракталов:1.Выбирается фор-ла, в нее подставляется число и
получается рез-т. 2.Получен. рез-т подставляется в эту же ф-лу и
получается следующее число.З.Повторяется эта же процедура много раз (итерационный процесс).4.В рез-те получается набор чисел, к-рые явл-ся точками фрактала.Мн-во Мандельброта-это фрактал, определенный как мн-во т-к на комплексной пл-ти, для к-рых итеративная п-ть: zo=0; zn+1=zn2+c, где с=х+ iy не уходит в беск-сть. Стохаистич. фракталы. Их получают, меняя в итерационном процессе нек-рые параметры случ.образом. Этим способом можно нарисовать такие природные объекты, как изрезанные береговые линии, рельеф местности, облака, волны на воде и мн.др. Поэтому фракт.модели сегодня широко применяются в комп.играх, создавая в них обстановку, к-рую уже трудно отличить от реальности.Слайд 32ЗГ. Фракт.разм-сть.опр. фрактал-мн-во с дробной размерностью.опр.(мандельброт)фракт-мн-во,размерн. Хаусдорфа-Безиковича кот-го строго больше тополог.разм.Типы:
1.размерность самоподобия опр.фор-лой где N -
число одинаковых частей на кот разбивается данный самопод объект, имеющий в n раз меньший пространственный размер. Кривой Кох - . Салф.Серп.N=3,n-2, Мн-во Кантора N=2,n=3 Фрактальная раз-ть (Хаусдорфа- Безиковича):мн-во А имеет paзм .d=dimA, 0 < d < 2, если при э —> 0 число клеток N(s)растет как С / эd, где С-конст,наз-мая d-мерой мн-ва А.прим:фрактал Кантора
прим: Салф.Серпин. Ков.Серп.:
пр: Кривая Кох
Метод "Систем Итерируемых Ф-й" метод появ.в сер. 80-х как простое средство получен фракт.стр-р.автор-амер.м-к Барнсли.
Слайд 334Г. Эл-ты теории узлов. Под УЗЛОМ поним-ся отр. веревки, расположенной
в трехмерном пр-ве, концы к-рой соединены. УЗЕЛ - это замкнутая
линия в пр-ве, гладкая или ломаная, к-рая м.б. как угодно закручена и переплетена. Под РАЗВЯЗ УЗЛА поним выпрямление этого отр. путем деформац. его в трехмерном пр-ве.Пр:-тривиальный узел,- узел «восьмерка». Два узла ИЗОТОПНЫ, если один узел можно перевязать в др., не разрезая его и не допуская самопересечений.Элементарные изотопии, а) Замена одного из звеньев узла двумя новыми отрезками, к-рые вместе с ним образуют контур тр-ка, пересекающегося с прежним узлом только по замененному звену, б) замена двух соседних звеньев одним отрезком, к-рый вместе с ними образует контур тр-ка, пересекающегося с прежним узлом только по заменяемым звеньям. Узел, изотопный контуру тр-ка (окр-ти), н-ся ТРИВИАЛЬНЫМ. Проблемы: 1. Проблема распутывания: найти алгоритм, к-рый по любой диаграмме узла узнает, тривиален узел или нет. При решении проблемы можно восп-ся операциями РЕЙДерместеРА, придуманными в 1920 г.Слайд 341. Идея алгоритма Рейдемейстера: сведение сложной простр-ной задачи развязывания узла
к более простой задаче применения операций к кривым на пл-ти.а)
раскручивание и закручивание петель; б) соскальзывание одной ветви с другой и налезание одной ветви на др.; в) переброс ветви ч/з двойную т-ку. Недостаток: алгоритм Рейдемейстера наз-ют жадным: он «жаден» до упрощения, он не думает вперед и на каждом шагу делает ход, добиваясь сиюминутного упрощения. Алгоритм Рейдемейстера не всегда умеет распутывать тривиальные узлы. 2. АЛГОРИТМ ПОЛНОГО ПЕРЕБОРА С ЗАПОМИНАНИЕМ (исп-ся в комп. программах): диаграмма узла рисуется на экране мышкой, а затем кодируетсякомпьютером в виде строки из чисел (номеров перекрестков), букв В, Н (обозначающих переход сверху или снизу) и знаков +,- (обозначающих ориентацию перекрестков).1(В-) 1(Н-) 2(В-)2(Н—)3(В+)3(Н+) 2(В-) 2(Н—) — уберет; 1(В-)1(Н-) уберет. — узел распутан. Недостаток: требует огромных ресурсов машинной памяти, ибо сильно ветвится и требует запоминания всех промежуточных ходов.Слайд 355Г. Проблема сравнения узлов. Проблема сравнения: найти алгоритм, к-рый по
любой пape диаграмм узнает, эквивалентны узлы или нет. С каждой
диаграммой узла необходимо связать нек-рый алгебраический объект - инвариант - так, чтобы диаграммам эквив-х узлов отвечали одинаковые инварианты. Инвариант н-ся ПОЛНЫМ, если его совпадение влечет эквив-ть узлов. Два узла ИЗОТОПНЫ, если один узел можно перевязать в другой, не разрезая его и не допуская самопересечений.Инварианты узла:1. МИНИМ ЧИСЛО СКРЕЩ УЗЛА. Из всех диаграмм узла В выбирают ту, д/к-рой число скрещиваний минимально. Это число М(В) и н-ся мин числ скрещ узла В. Этот инвариант полным не явл-ся.ПОЛИНОМ КОНВЕЯ.Конвей постулировал: каждой диаграмме узла L поставлен в соот-вие полином от переменных х с целыми коэффициентами PL(x). При этом должны выполняться 3 акс. 1)Эквив-ным диаграммам отвечает один и . тот же полином,2)Тривиальному узлу отвечает полином нулевой степени, 3)Трем зацеплениям L+ L – I0 которые всюду одинаковы кроме небольшого кружочка, отвечают полиномы, связанные соотношением:Слайд 36
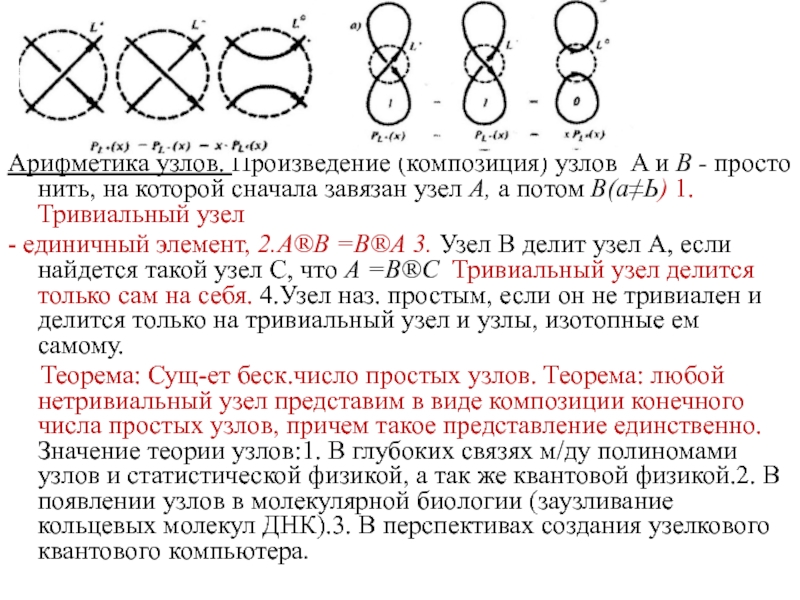
Арифметика узлов. Произведение (композиция) узлов A и В - просто
нить, на которой сначала завязан узел А, а потом В(а≠Ь)
1.Тривиальный узел- единичный элемент, 2.А®В =В®А 3. Узел В делит узел А, если найдется такой узел С, что А =В®С Тривиальный узел делится только сам на себя. 4.Узел наз. простым, если он не тривиален и делится только на тривиальный узел и узлы, изотопные ем самому.
Теорема: Сущ-ет беск.число простых узлов. Теорема: любой нетривиальный узел представим в виде композиции конечного числа простых узлов, причем такое представление единственно. Значение теории узлов:1. В глубоких связях м/ду полиномами узлов и статистической физикой, а так же квантовой физикой.2. В появлении узлов в молекулярной биологии (заузливание кольцевых молекул ДНК).3. В перспективах создания узелкового квантового компьютера.
Слайд 376Г. Элементы теории кос. Мат. коса состоит из n нитей
(т.е. кривых в пр-ве), к-ые нач-ся в n точках гориз-ой
прямой и заканч-ся в n точках др. гориз-ой прямой, расположенной ниже. При этом нити должны быть нисходящими, т.е. касательный вектор в любой точке кривой должен все время «смотреть вниз», ему запрещается быть гориз-ым и тем более «смотреть вверх».Девичья коса(123\321) (2).Приимер фигур, не являющихся косами(3). Крашенной косой наз-ся любая коса, которой отвечает перестановка номеров (123….\123…) Тривиальная коса - коса, все нити котторой вертикальные прямые. Циклические косы - косы, переставляющие все номера нитей по единому циклу, например: 1-2-4-3-1.
Теорема Александера: Любой узел - это замкнутая коса.
Алгебра кос. Произв-ем 2 кос с одинаковым числом нитей наз-ся коса, полученная след, образом: нижние концы нитей 1ой косы соединяют с верхн. концами 2ой косы, получ-ую косу сжимают в 2раза в вертик-ом напр-ии.
Слайд 38Теорема о косах: Умножение кос обладает след, св-ми: 1. (асс-ть)
для любых кос а, b и с: (а • Ь)
• с = а • (Ь • с); 2. (наличие единицы) сущ-т такая коса 1, что для любой косы а: а*1=а=1*а 3. (наличие обратного эл-та) для любой косы b найдется такая коса Ь-1, что ЪЪ -1 = 1 = Ъ-1Ъ. Иными словами, косы образуют группу. Эта группа некомм. утативна.Знач-ие теории узлов и кос: 1. В глубоких связях между полиномами узлов и статистической физикой («модель Поттса» для льда), а также квантовой физикой; 2. в появлении узлов в молекулярной биологии (заузлевание кольцевых молекул ДНК). В перспективах создания узелкового квантового компьютера.
Слайд 397Г. Прямолинейные и криволинейные симплексы. Гомотопия - непрерывная деформация объекта,
при к-ой разрешены "склейки", но запрещены "разрывы". Onpl: Отображение одной
фигуры на др. наз-ся гомеоморфизмом, если оно устанавливает взаимно-однозначное и взаимно-непрерывное соответствие между точками обеих фигур. Примеры гомеом-ых фигур: прямолин-ый отрезок и непрерывная дуга: квадрат и круг; куб и тетраэдр; плоскость и сфера с одной выколотой (выброшенной) точкой. Опр2:Нульмерным симплициальным комплексом (нульмерным полиэдром) наз-ся конечная система точек (его «вершин»). ОпрЗ: Одномерным симплициальным комплексом или графом (одномерным графом) наз-ся система, состоящая из конечного числа Ао точек («вершин») и конечного числа А1 простых дуг (его «ребер»). При этом: 1. Любые 2 ребра или не имеют общих точек, или пересекаются только своими вершинами. ребер. Опр 7: Простым циклом наз-ся связный граф, у к-го все вершины имеют индекс 2. Простой цикл гомеоморфен окружности.Слайд 40Понятие n-мерного симплекса. Барицентрические координаты. Пусть Ао, ..., Ап -
система линейно- независимых точек
евклидова пространства Rn+1. Поместим в каждую точку Ai неотриц-ую массу mi, так чтобы mo+...+mn=l. Опр: Центром тяжести этих масс (точек) явл-ся точка А - конец вектора ОА , где ОА=moOAo+...+mnOAn,, О- начало координат. Числа mо, ..., mп наз-ся барицентрическими координатами. Меняя массы m0, ..., mп, заставляем точку А менять свое положение. В рез-те она пробегает некотор. мн-во, к-ое наз-ся п-мерным (прямолинейным или евклидовым) симплексом. Прямолинейный (или евклидовый) симплекс явл-ся выпуклой оболочкой точек Ао, ..., Ап. Нульмерный симплекс изобр-ся точкой; одномерный симплекс - отрезком на пл-ти; двумерный симплекс - треуг-ом в трехмерном пр-ве; трехмерный симплекс - заполненным тетраэдром в трехмерном пр-ве. В алг-ой топологии рассм-ют не только сами прямолинейные симплексы, но и их всевозможные гомеоморфные образы - топологические или криволинейные симплексы.Слайд 41 Криволинейный симплексы образуют конечное симплициальное разбиение мн-ва X, если
выполнены 2 условия: 1) симплексов конечное число и каждая точка
мн-ва X попадает в некотор. симплекс (покрыта некотор. симплексом); 2) 2 симплекса либо вообще не пересекаются (не имеют общих точек), либо один из них явл-ся гранью другого, либо они имеют общую грань, являющуюся пересечением этих симплексов.«Pапрещенные» ситуации:
Если некоторое.мн-во точек евклидова пр-ва (более общо, топологическое пр-во) разбито на симплексы так, что выполнены усл-ия 1 и 2, то такое мн-во наз-ся полиэдром. Примеры полиэдров: 1. Евклидово пр-во - бесконечный полиэдр. Пример замощения плоскости. 2. Плоское кольцо, лист Мебиуса- полиэдры. 3.Окр-сть и двумерная сфера - полиэдры. Двумерные сферы с некоторым числом. Сфера представлена в виде полиэдра - в виде границы плиты.В плите высверлена квадратная дыра. Полученный двумерный полиэдр гомеоморфен - тору (двумерному тору). Тор - полиэдр. Бутылка Клейна - полиэдр.
Слайд 4320. Алгебраические числа. def: Комплексное число называется алгебраическим , если
оно является корнем ненулевого многочлена с целыми коэффициентами, и трансцендентным
в противном случае. Например, рациональное число является корнем линейного многочлена, число вида является корнем многочлена , где а – рациональное число, число i – корень многочлена и т.д. Одно и то же число α может быть корнем различных многочленов с рациональными коэффициентами. Обозначим множество таких многочленов через Iα: Iα= {fQ[x]: f(α)=0}. Очевидно, Iα – идеал в кольце Q[x]: если f Iα и h Q[x], то и если f Iα и g Iα, то . Если алгебраическое число α является корнем некоторого многочлена с целыми коэффициентами, то оно является и корнем хотя бы одного из делителей этого многочлена, который также является многочленом с целыми коэффициентами.Кольцо многочленов Q[x] является кольцом главных идеалов, поэтому идеал Iα порождается некоторым многочленом рα, который называется минимальным многочленов числа α и является многочленом наименьшей степени.
Слайд 44Теорема 1. Минимальный многочлен рα является неприводимым над полем Q.
Док-во. Пусть рα приводим, т.е.
,. Так как , то или . Но тогда , что противоречит тому, что рα – многочлен наименьшей степени. Теорема 2. Минимальный многочлен рα определен единственным образом. Док-во. Пусть , где f(x) и g(x) неприводимы над полем Q. Тогда НОД(f,g)≠1 и, следовательно, эти многочлены, являясь неприводимыми, могут отличаться друг от друга лишь множителем нулевой степени.
Теорема 3. Минимальный многочлен не имеет кратных корней.
Док-во. Так как минимальный многочлен неприводим в кольце Q[x], то он взаимно прост со своей производной, следовательно, все его корни простые. Def: Степень минимального многочлена рα называется степенью алгебраического числа α. Def: Алгебр. числа, являющиеся корнями одного и того же неприводимого многочлена, называются сопряженными.
Таким образом, множество алгебраических чисел распадается на непересекающиеся конечные классы сопряженных между собой чисел.
Слайд 4521.Квадратичные вычеты и невычеты. Рассмотрим двучленные сравнения второй степени следующего
вида:
. (4) Если сравнение (4) имеет решение, то а называют квадратичным вычетом, в обратном случае — квадратичным невычетом. Например, число 2 является квадратом по модулю 7, так как 42=16≡2(тоd 7), значит, 2 – квадратичный вычет. Число 3 является квадратичным невычетом по модулю 7, т.к. сравнение х2≡3(тоd 7) решений не имеет. Если а — квадратичный вычет по модулю р, то сравнение (4) имеет два решения. Действительно, если а – квадратичный вычет по модулю р, то у сравнения х2≡а(тоd р) есть хотя бы одно решение х≡х1 (тоd р). Тогда х2 =- х1– тоже решение, так как . Второе решение отлично от первого, так как из мы имели бы , что невозможно ввиду того, что р не делится на 2. Теорема (критерий Эйлера). Если а не делится на р (р>2), то сравнение (4) имеет или два решения, или не имеет ни одного,— в зависимости от того, будет ли (5)(6)
Слайд 46Доказательство. Докажем сначала, что а непременно удовлетворяет одному и только
одному из сравнений (5) и (6). Именно, по теореме Ферма-Эйлера
, отсюда:Исходя из того, что произведение (двух или нескольких чисел) делится на простое число р тогда и только тогда, когда по крайней мере один из сомножителей делится на р, можем сказать, что по крайней мере один из сомножителей или делится на р. Оба одновременно не могут делиться на р, так как их разность = +\-2 не делится на нечетное число р. Следовательно, а удовлетворяет одному и только одному сравнению (5), (6). Пусть сравнение (4) имеет решение х; тогда и (—х) или (р — х) — тоже решение, ибо
. Эти два решения различны по модулю р: х очевидно, не делится на р (ибо х2 — а делится на р). Если бы было х ≡ – х (mod р), то мы имели бы: , а этого не может быть, так как ни 2, ни х не делятся на р. Больше двух решений сравнение 2-й степени с простым модулем не может иметь. Возведя обе части сравнения (4) в -ю степень, получим:
Слайд 47Но по теореме Ферма-Эйлера
, следовательно, если сравнение (4) имеет
корни, то а непременно удовлетворяет сравнению (5). С другой стороны, если найти квадраты чисел 1, 2, 3, ... р— 1, то среди этих квадратов будут только (p-1)\2 чисел, различных по модулю р, так как числа α и р — α≡ — α дают одинаковые (по модулю р) квадраты, и кроме этих двух чисел ни одно из чисел 1, 2, ... р — 1 не даст такой же квадрат (иначе сравнение (4) имело бы больше двух различных корней). Обозначим эти различные по модулю р квадраты чисел 1, 2, ... р—1 так: (7) Если а равно одному из чисел (7), то сравнение (4) имеет решение, следовательно, все числа (7) удовлетворяют сравнению (5). Но сравнение (5) не может иметь больше чем (p-1)\2 различных (по модулю р) решений, следовательно, оно имеет как раз (p-1)\2 различных решений, и при а, равном любому из них, сравнение (4) имеет решения. Отсюда же следует, что и сравнение (5) имеет тоже (p-1)\2 различных (по модулю р) решений, и при а, равном любому из этих решений, сравнение (4) не имеет решений. Т/ доказана.Слайд 4822. Мультипликативные функции Def. Функция θ: R → R (или
θ: C → C ) называется мультипликативной если: 1). Функция
θ определена всюду на N и существует аN такое, что θ(а)≠0.2) Для любых взаимно простых натуральных чисел а1 и а2 выполняется θ(а1 · а2) = θ(а1) · θ(а2). Свойства мультипликативных функций: 1. θ (1) = 1. Док-во. Пусть а - то самое натуральное число, для которого θ(а) ≠0. Тогда θ (а ·1) = θ (а) · θ(1) = θ (а). 2. где р1, р2,..., рn – различные простые числа. 3. Произведение нескольких мультипликативных функций является мультип. функцией. Док-во. Сначала докажем для двух сомножителей: Пусть θ1 и θ2 – мультип. функции θ=θ1·θ2, тогда (проверяем аксиомы опр-ния)
1) θ (1) = θ1(1) · θ2(1) = 1 и, кроме того, существует такое a (это a =1), что θ(a)≠ 0. 2) Пусть НОД( a , b ) = 1 – т.е. числа а и b взаимно просты. Тогда θ ( a · b ) = θ 1 ( a · b ) · θ 2 ( a · b ) =
= θ 1 ( a ) ·θ 1 ( b ) ·θ 2 ( a ) · θ 2 ( b ) = θ1(a) · θ2(a) · θ1 (b) · θ2 (b) = θ(a) · θ(b). Док-во для большего числа сомножителей проводится стандартным индуктивным рассуждением.
Слайд 49Лемма 1. Пусть
– каноническое разложение числа
aN , Θ - любая мультипликативная функция. Тогда:Если a = 1, то считаем
правую часть равной 1.
Док-во. Раскроем скобки в правой части. Получим сумму всех (без пропусков и повторений) слагаемых вида где , для всех . Так как различные простые числа заведомо взаимно просты, то
, а это как раз то, что стоит в доказываемом равенстве слева. Лемма 2. Пусть Θ(a) - любая мультип. функция. Тогда – также мультип. функция.
Примеры мультипликативных функций .П1. Число делителей данного числа. Пусть – тождественная единица (заведомо мультип.функция). Тогда, если , то тождество леммы 1 принимает вид: - это не что иное, как количество делителей числа a. По лемме 2, количество делителей τ(a) числа a есть мультипликативная функция.
Слайд 50Пример 2. Сумма делителей данного числа. Пример 3. Функция Мебиуса.
Функция Мебиуса μ(a) - это мультип. функция, определяемая следующим образом:
для простого рна остальных натуральных числах функция доопределяется по мультип. Таким образом, если число a делится на квадрат натурального числа, отличный от единицы, то μ(a)=0; если же a=p1·p2·…·pn то μ(a) =(–1)п, где п - число различных простых делителей a. μ(1)=(–1)0=1.
Лемма 3. Пусть Θ(a) – произв. мультип. функция, Тогда: (при a = 1 считаем правую часть равной 1).
Пример 4. Функция Эйлера. Функция Эйлера φ(a) есть количество чисел из ряда 0, 1, 2,..., a – 1, взаимно простых с a.
Слайд 5123 Понятие поля. Def. Полем называется коммутативное ассоциативное кольцо с
единицей без делителей нуля, в котором 0 ≠1 и любой
ненулевой элемент обратим.Def/. Алгебра2. 3.
4.
5. 6. 7.
8. 9.
Примеры полей Бесконечные поля: – поле рациональных чисел; – поле действительных чисел; – поле комплексных чисел. Конечные поля: – поле вычетов по модулю 2. Теорема. Конечная область целостности является полем. Пусть К – коммутативное кольцо с единицей без делителей нуля. Докажем, что любой его ненулевой элемент обратим. Рассмотрим последовательность до тех пор, пока какой-нибудь элемент не повторится
Слайд 52Пусть
. К – область целостности, следовательно операция умножения сократима, следовательно,
. Т. о, . Теперь покажем, что , так как К – область целостности, и т.д. Т.о, ,следовательно, . Таким образом,
, следовательно, любой ненулевой элемент обратим, следовательно К является полем. Характеристика поля Пусть
Def. Минимальное положительное число п, для которого n*1=0, называется характеристикой поля. Если
, то поле называют полем с нулевой характеристикой. Пример 1. Поле рациональных чисел – поле с нулевой характеристикой: char Q = 0. Пример 3. Поле вычетов по модулю р, где р – простое число – поле характеристики р: , char P = p. Простое поле Def. Множество M поля P называется подполем P, если оно само явл. полем при тех же операциях сл. и умн., которые заданы в поле P. Тогда P называется расширением поля M.
Слайд 53Пр1. Поле рацион. чисел является подполем поля действ чисел.
Пр2. Поле
действ. чисел является подполем поля компл. чисел.
Def. Поле, не имеющее
подполей, отличных от него самого, называется простым. Примерами простых полей могут служить поле рацион. чисел и поля вычетов по простому модулю p. Действительно, любое подполе M поля Q рациональных чисел содержит число 1, а значит, и все его кратные n · 1 = n, т. е. все целые числа, а значит, и все их частные, т. е. все рацион. числа. След., M = Q, т. е. Q – простое поле. Точно так же любое подполе M поля Zp вычетов по простому модулю p содержит класс (1), служащий единицей Zp, а значит, любой класс (r) как r-кратное класса (1). Итак, M = Zp, т. е. Zp – простое поле. Имеет место следующий результат: любое поле содержит простое поле, и притом только одно.Расширение поля… Пусть поле P – расширение поля M. Превратим поле Р в векторное пространство над полем М: будем считать элементы поля Р векторами, элементы поля М скалярами: сопоставим и вектор , равный обычному произведению элементов из поля Р.
Слайд 54Если размерность этого векторного пространства конечна, то Р называется конечным
расширением поля М, а называется
степенью этого расширения и обозначается [P:M]. Пр. Пусть С, R, Q – поля компл. и действ. чисел соответственно. Тогда [C:R] = 2. Теорема. Пусть – последовательные расширения поля L. Если М – конечное расширение поля L, а Р – конечное расширение поля М, то Р – конечное расширение поля L, причем если и . Алгебраические элементы. Def. Элемент α расширения Р поля М называется алгебр. (над М), если существует ненулевой многочлен f(x) €М[x], такой, что f(α) =0. Расширение Р поля М называется алгебраическим, если все его элементы алгебраические. Если алгебр-ий элемент α является корнем некоторого многочлена с целыми коэфф., то он является и корнем хотя бы одного из делителей этого многочлена, который также является многочленом с целыми коэффициентами.Неприводимый многочлен наименьшей степени, не имеющий кратных корней, для которого f(α) =0 называется минимальным многочленов элемента α.
Слайд 5525. Билинейные формы. 1. Билинейные формы. Пусть L – линейное
пространство над полем Р. Def. Билинейной формой векторов х,у пространства
L называется отображение А: L L→ Р – линейное по каждому вектору, т.е. 1.2. 3. 4.
Ex. Пусть L – линейное пространство п-мерных арифметических векторов над полем действительных чисел, , – произвольные векторы этого пространства, – произвольная квадратная матрица с действительными элементами. Тогда функция – билинейная форма.
Def. Билинейная форма называется симметрической, если она не меняется при перестановке своих переменных, и кососимметрической, если при перестановке переменных она меняет знак: – симметрическая форма,
– кососимметрическая форма. Например, скалярное произведение в евклидовом пространстве – симметрическая билинейная форма.
Слайд 56Матрица билинейной формы. Пусть L – линейное пространство над полем
Р,
– произвольный базис этого пространства, . Пусть векторы х и у имеют в этом базисе координаты и соответственно. Тогда по определению билинейной формы имеем:Def. Матрица , где называется матрицей билинейной формы А(х,у) в базисе . Таким образом, в каждом базисе билинейная форма А(х,у) однозначно определяется своей матрицей .
Изменение матрицы билинейной формы при изменении базиса. Пусть L – линейное пространство над полем Р, ,
– произвольные базисы этого пространства. По определению, матрицей перехода от базиса {e} к базису {u} называется матрица координат новых базисных векторов в старом базисе, т.е. , где
Слайд 57Ранг билинейной формы. Невырожденные формы. Из формулы
,
связывающей матрицы билинейной формы в разных базисах, следует, что ранг матрицы билинейной формы не зависит от базиса. Таким образом, рангом билинейной формы называется ранг ее матрицы в произвольном базисе:. Билинейная форма называется невырожденной, если ее ранг равен размерности пространства и вырожденной в противном случае. Ядро билинейной формы. Левым (правым) ядром билинейной формы называется множество
Как левое, так и правое ядро билинейной формы является подпространством пространства L. Размерности левого и правого ядра равны между собой, причем имеет место соотношение: .
Слайд 6012. Алгебра Ли над полем. Опр. Векторное пространство L над
полем Р с операцией LLL, обозначаемой (x,y)[x,y] называется алгеброй Ли,
если выполняются следующие аксиомы:Операция скобки билинейна: , ,
, ; 2. [x,x]=0; 3. Выполняется тождество Якоби: [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0. Из 1-2 вытекает свойства антикоммутативности: [a,b]=–[b,a]: По опр.(акс. 2),
.С другой стороны, на основании аксиомы (1), имеем: Таким образом, = 0, откуда [a,b]=–[b,a].Примеры алгебр Ли. Пр1. Вект. простр. «геометр.» векторов трехмерного пространства над полем действ. чисел с операцией векторного произведения: множество векторов с операциями сложения и векторного умножения является неассоциативным, некоммутативным кольцом, векторное умножение дистрибутивно относительно сложения, векторный квадрат вектора равен нуль-вектору, тождество Якоби выполняется.
Слайд 61Пр2. Любое ассоциативное кольцо можно сделать алгеброй Ли, изменив его
умножение:
.1. Проверим дистрибут.:2. Проверим 2 акс.: . 3. Проверим тождество Якоби:
Пр 3. Пусть L – конечномерное линейное пространство над полем Р. Обозначим через End (L) алг.лин. опер-ов, действу-их в простр. L с опер. суперпозиции в качестве умнож-я. Как векторное пространство, она имеет размерность п2. Введя операцию , получим алгебру, называемой линейной алгеброй Ли.
Приведем примеры других линейных алгебр Ли. Они распадаются на 4 семейства Al, Bl, Cl, Dl и называются классическими алгебрами Ли. Алгебра Ли Al состоит из операторов пространства L с нулевым следом и называется специальной линейной алгеброй Ли.
Слайд 62Алгебры Bl и Dl – алгебры ортогональных операторов, действующих в
нечетно- и четномерном пространствах соответственно (ортогональный оператор – оператор, для
которого сопряженный совпадает с обратным).Иногда бывает удобно рассматривать алгебры Ли абстрактно. Например, если L – абстрактное векторное пространство с базисом е1, е2, …, еn, то его можно превратить в алгебру Ли, задавая коммутатор на базисных векторах при помощи структурных констант формулами:
. Более того, константы , у которых , восстанавливаются по остальным структурным константам в силу аксиом из определения алгебры Ли. Легко показать, что любое множество констант, удовлетворяющих следующим очевидным ограничениям, задает структуру алгебры Ли на произвольном п-мерном векторном пространстве: , . Более того, любой набор констант задает на векторах базиса операцию, однозначно продолжаемую до структуры алгебры Ли на всем векторном пространстве.


























































![1Наука. В философии наука рассм-ся как одна из форм обществ-го c ознания 12. Алгебра Ли над полем. Опр. Векторное пространство L над полем 12. Алгебра Ли над полем. Опр. Векторное пространство L над полем Р с операцией LLL, обозначаемой (x,y)[x,y]](/img/thumbs/2a26ba878b00eaa0ec0e9c8adb9c8583-800x.jpg)






















