Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Частица в ящике
Содержание
- 1. Частица в ящике
- 2. Стационарный базисФ(x, t) = D1 ⋅ ψ1
- 3. Стандартный объект — «частица» (т.е. внутреннее строение
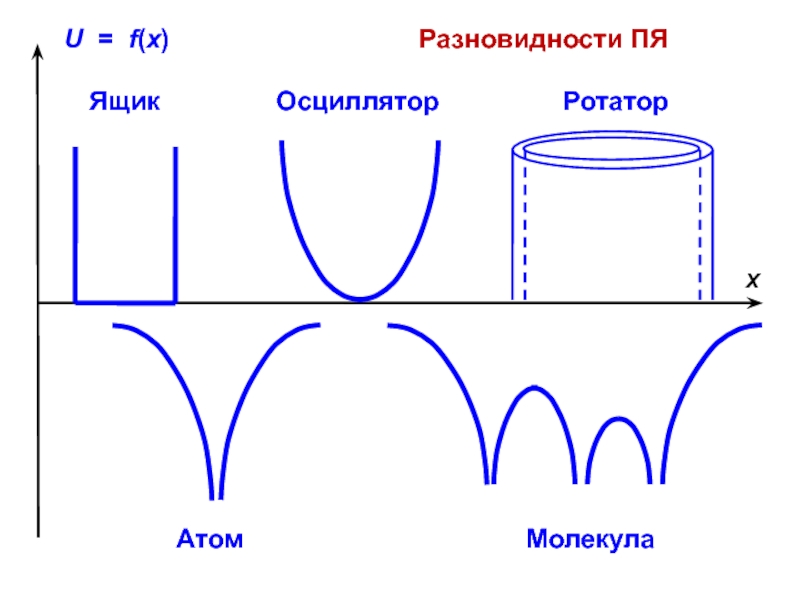
- 4. Разновидности ПЯ
- 5. Частица в «потенциальном ящике» (прямоугольной потенциальной яме) Возвратно-поступательное движение
- 6. ИМПУЛЬС, направленный вдоль оси Х, который может
- 7. Адиабатический инвариантУсловие адиабатичности: скорость перемещения стенки должна быть малой по сравнению со скоростью движения частицыVстенки
- 8. Адиабатический инвариантAi = Р ⋅ L =
- 9. Квантовомеханическое описаниеЗадача: найти все возможные состояния (способы
- 10. Уравнение на собственные значения для НЛюбая точка
- 11. Граничные условияВнутри ящика волновая функция может иметь
- 12. ψ(х) = А ⋅ е ikx +
- 13. ψ(х) = А ⋅ е ikx +
- 14. Вывод: для частицы в ящике стационарными являются
- 15. Нестационарные состоянияНестационарные состояния (А ≠ –В) за малое время вырождаются в одно из стационарных
- 16. Волновые функцииψ(х) ~ sin[(πn/L)x]
- 17. ψ(n = 0) = sin[(π0/L)х] = 0
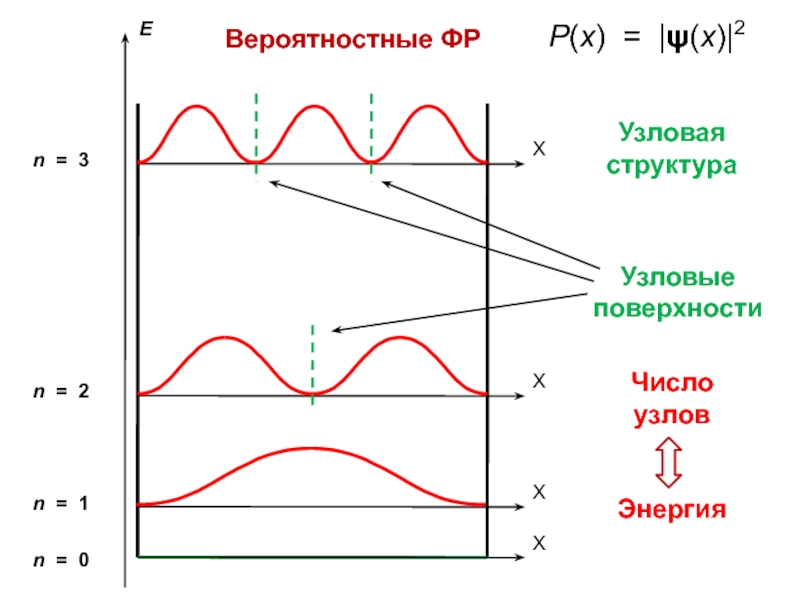
- 18. Вероятностные ФРP(x) = |ψ(х)|2Узловая структура
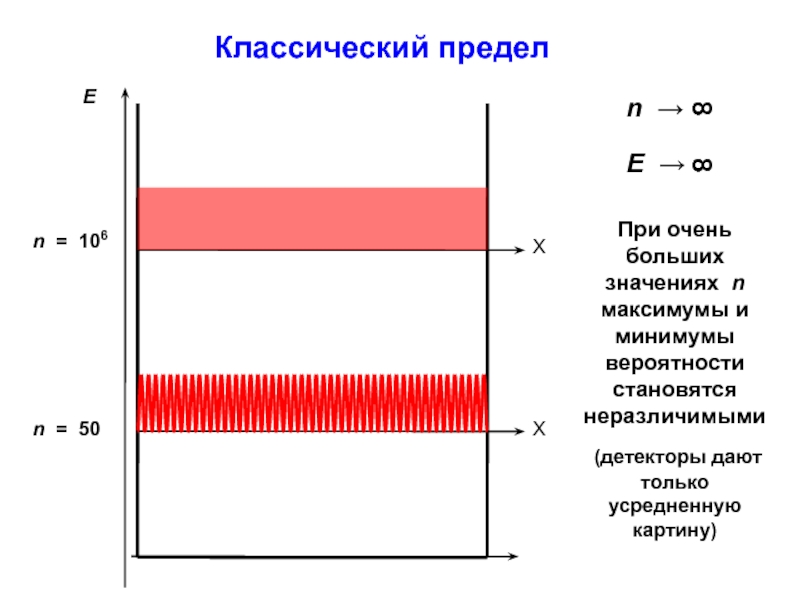
- 19. Классический пределПри очень больших значениях n максимумы
- 20. Влияние массы частицыМолекула D2Молекула T2Молекула Н2
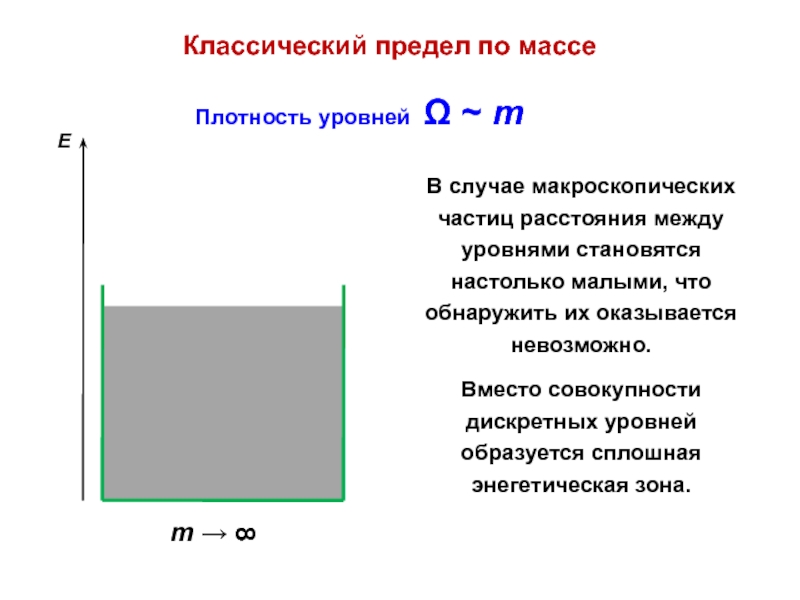
- 21. Плотность уровней Ω ~ mКлассический предел по массе
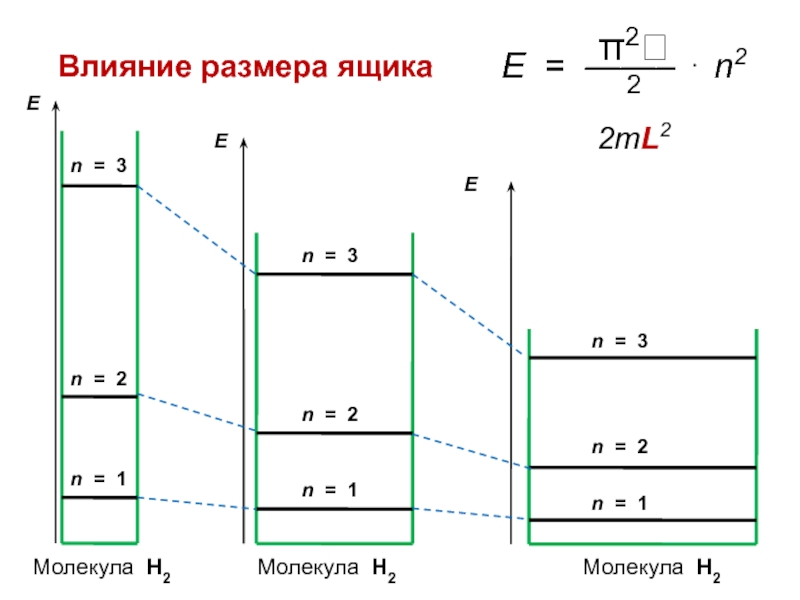
- 22. Влияние размера ящика
- 23. Плотность уровней Ω ~ L2В случае
- 24. Влияние размера ящикаАтом: L ≈ 10–10 мАтомное
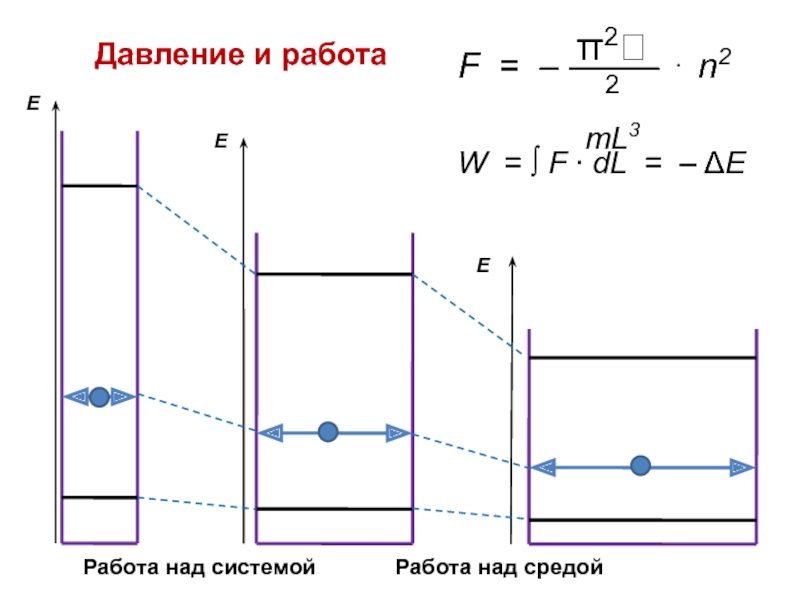
- 25. Давление и работаРабота над системойРабота над средойW = ∫ F ∙ dL = – ΔE
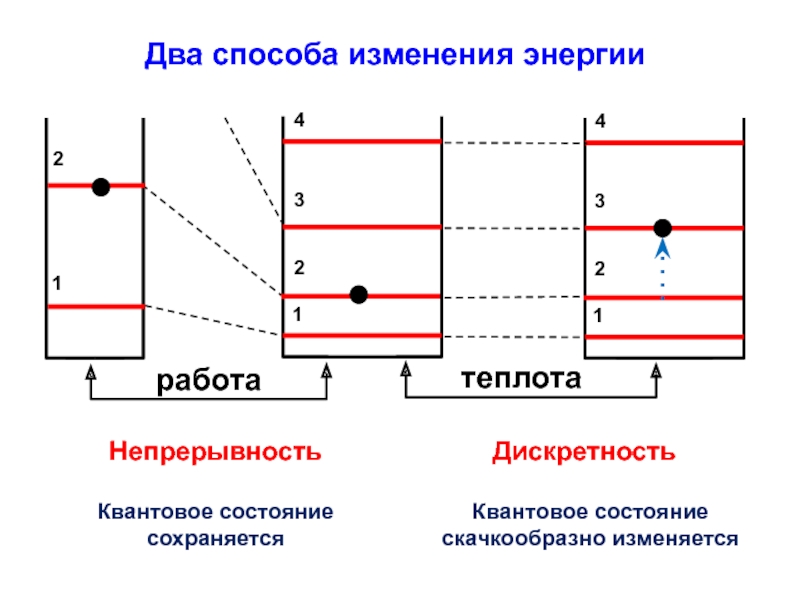
- 26. Два способа изменения энергииНепрерывностьКвантовое состояние сохраняется
- 27. Природа химических связей
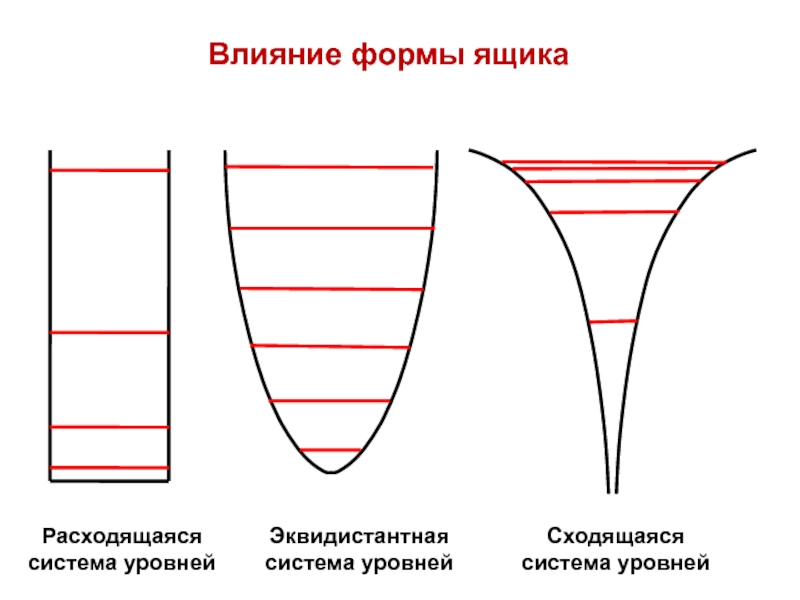
- 28. Влияние формы ящика
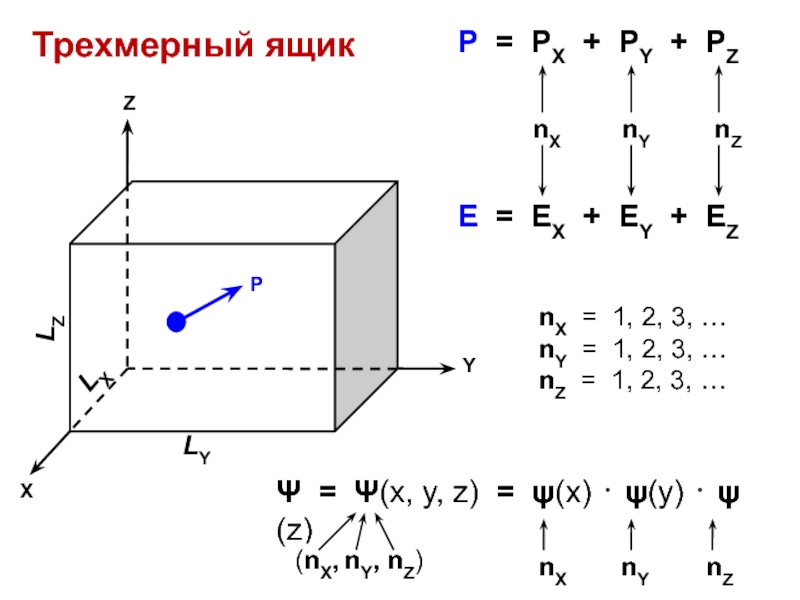
- 29. Трехмерный ящикΨ = Ψ(x, y, z) =
- 30. Трехмерный ящик( V = Lx ⋅ Ly ⋅ Lz — объем ящика )
- 31. nX = 3 nY = 2 nZ = 1
- 32. Пространство внутри трехмерного ящика разбивается узловыми плоскостями
- 33. Домашнее заданиеЗадача 4.1. В трехмерном потенциальном ящике
- 34. Задача 4.2. В трехмерном потенциальном ящике с
- 35. Задача 4.3. В трехмерном потенциальном ящике с
- 36. Скачать презентанцию
Стационарный базисФ(x, t) = D1 ⋅ ψ1 + D2 ⋅ ψ2 + . . . + Dr ⋅ ψr2. Только стационарные состояния являются долгоживущими, поэтому все объекты, участвующие в медленных химических
Слайды и текст этой презентации
Слайд 1Общая методика решения КМ-задач
ЗАДАЧА: найти все возможные состояния объекта (векторы
состояния или волновые функции Ф1, Ф2, …, Фn)
Слайд 2Стационарный базис
Ф(x, t) = D1 ⋅ ψ1 + D2 ⋅
ψ2 + . . . + Dr ⋅ ψr
2. Только
стационарные состояния являются долгоживущими, поэтому все объекты, участвующие в медленных химических процессах (атомы, ионы, молекулы), заведомо находятся в стационарных состояниях.3. Стационарные состояния удобно изучать экспериментально (большинство приборов действуют относительно медленно). При этом обеспечивается большая точность и надежность измерений.
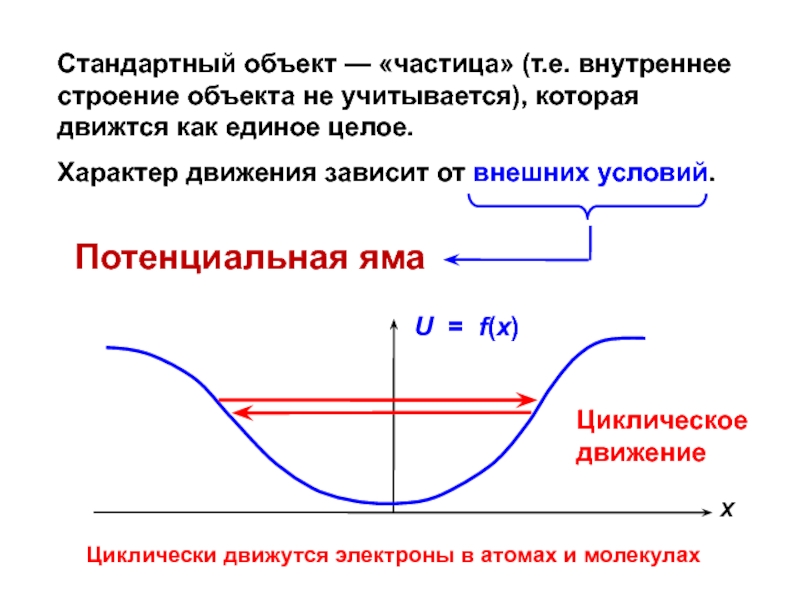
Слайд 3Стандартный объект — «частица» (т.е. внутреннее строение объекта не учитывается),
которая движтся как единое целое.
Характер движения зависит от внешних условий.
Циклически движутся электроны в атомах и молекулах
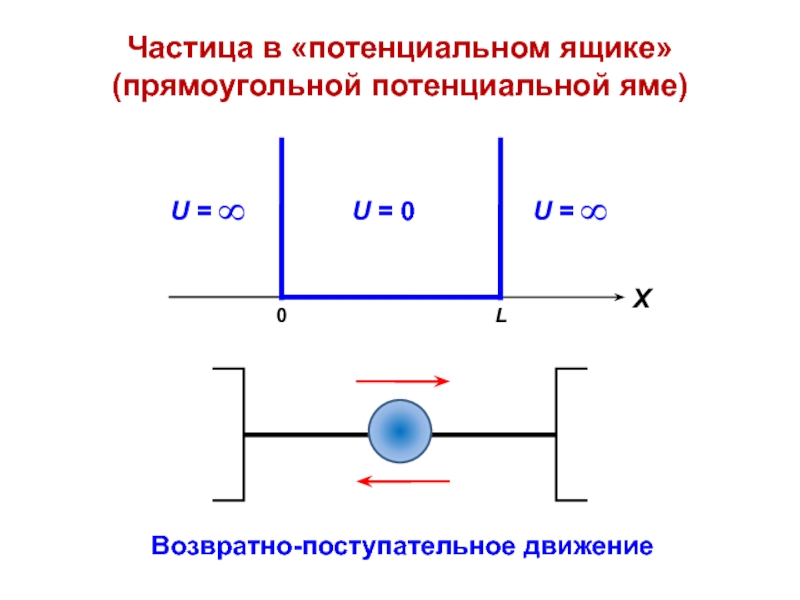
Слайд 5Частица в «потенциальном ящике» (прямоугольной потенциальной яме)
Возвратно-поступательное движение
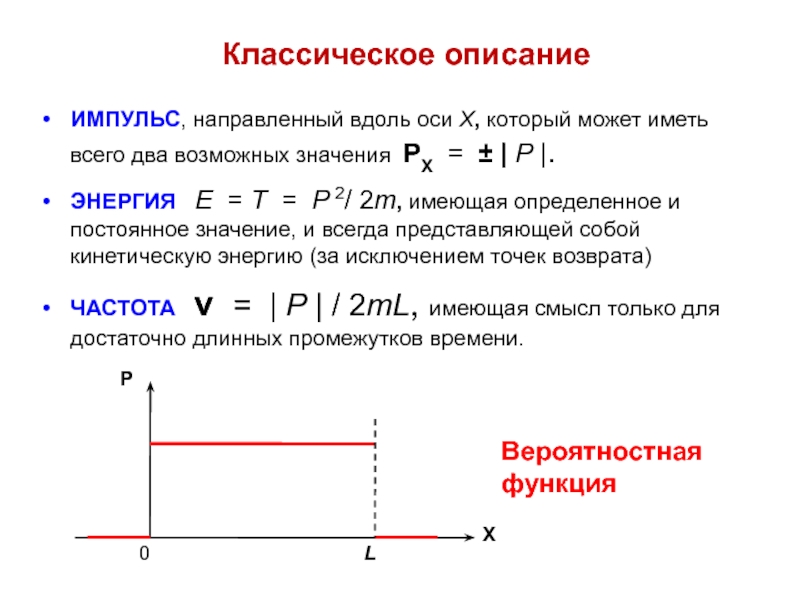
Слайд 6ИМПУЛЬС, направленный вдоль оси Х, который может иметь всего два
возможных значения РХ = ± | Р |.
ЭНЕРГИЯ
Е = Т = Р 2/ 2m, имеющая определенное и постоянное значение, и всегда представляющей собой кинетическую энергию (за исключением точек возврата)ЧАСТОТА ν = | Р | / 2mL, имеющая смысл только для достаточно длинных промежутков времени.
Классическое описание
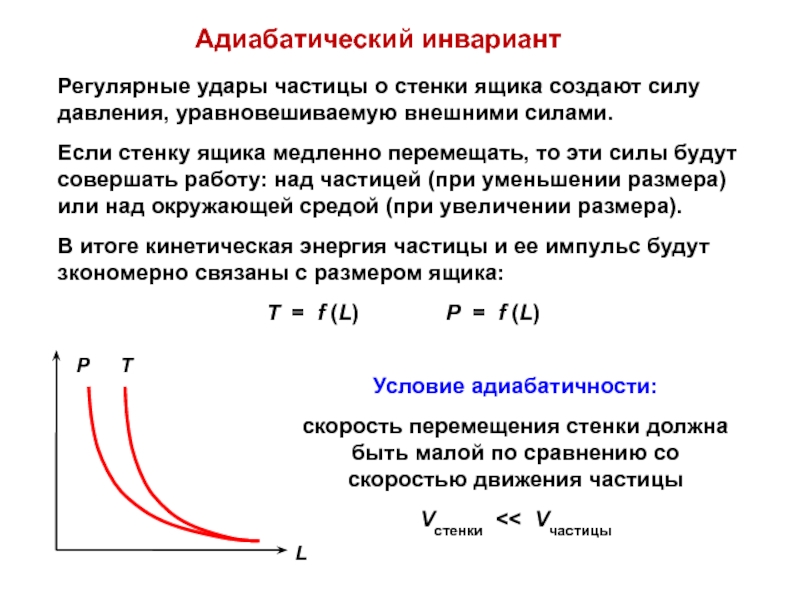
Слайд 7Адиабатический инвариант
Условие адиабатичности:
скорость перемещения стенки должна быть малой по
сравнению со скоростью движения частицы
Vстенки
стенки ящика создают силу давления, уравновешиваемую внешними силами.Если стенку ящика медленно перемещать, то эти силы будут совершать работу: над частицей (при уменьшении размера) или над окружающей средой (при увеличении размера).
В итоге кинетическая энергия частицы и ее импульс будут зкономерно связаны с размером ящика:
T = f (L) Р = f (L)
Слайд 8Адиабатический инвариант
Ai = Р ⋅ L = const
Р =
Ai / L
Т = Ai2 / 2mL2Чем меньше размер ящика, тем больше импульс и кинетическая энергия (и наоборот)
Если уменьшить размер ящика в два раза, то импульс и скорость увеличаться вдвое, а энергия — вчетверо.
Частота ( ν = Р/2mL ) также возрастет вчетверо (увеличение скорости в 2 раза и уменьшение длины пути в цикле в 2 раза).
Слайд 9Квантовомеханическое описание
Задача: найти все возможные состояния (способы движения) частицы в
ящике;
для каждого состояния установить вид волновой функции и допустимые
значения наблюдаемых: φ(x, t) = ? E = ? P = ?
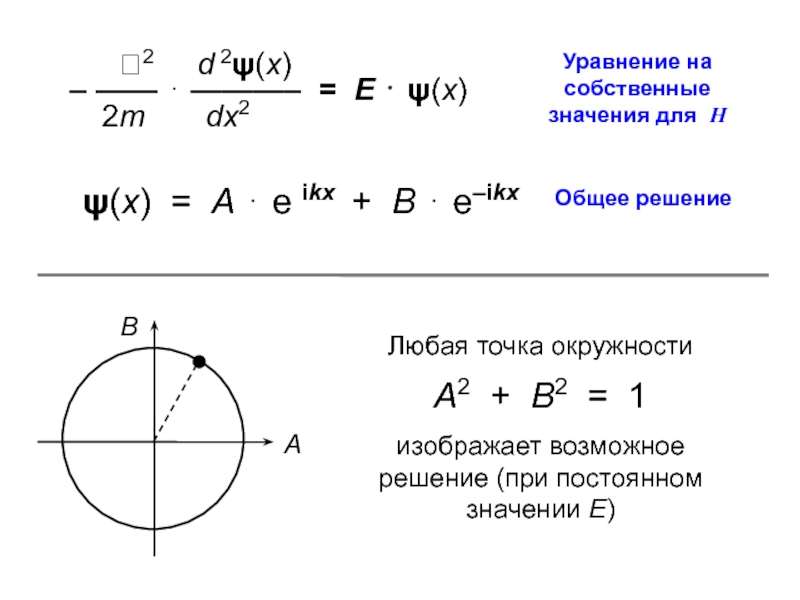
Слайд 10Уравнение на собственные значения для Н
Любая точка окружности
А2 + В2
= 1
изображает возможное решение (при постоянном значении Е)
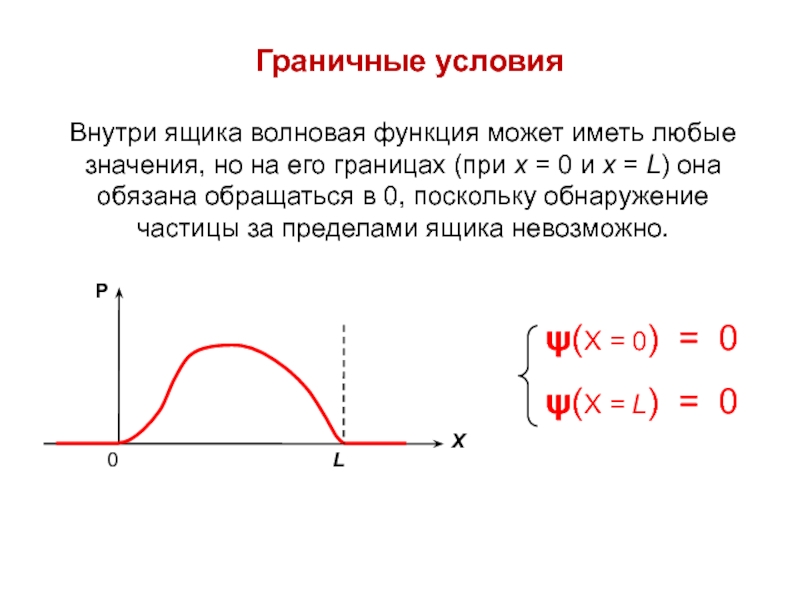
Слайд 11Граничные условия
Внутри ящика волновая функция может иметь любые значения, но
на его границах (при х = 0 и х =
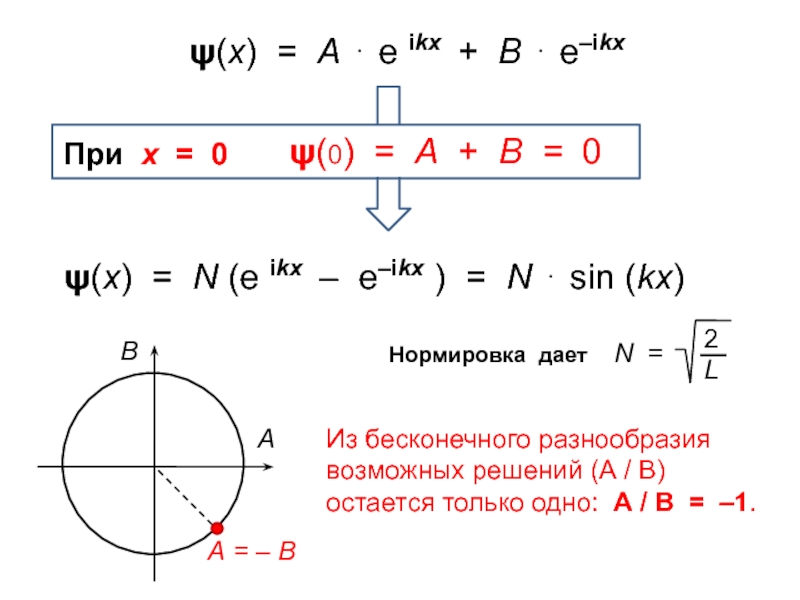
L) она обязана обращаться в 0, поскольку обнаружение частицы за пределами ящика невозможно.
Слайд 12ψ(х) = А ⋅ е ikx + В ⋅ e–ikx
ψ(х)
= N (е ikx – e–ikx ) = N ⋅
sin (kx)Из бесконечного разнообразия возможных решений (А / В) остается только одно: А / В = –1.
Слайд 13ψ(х) = А ⋅ е ikx + В ⋅ e–ikx
ψ(х)
= N (е ikL – e–ikL ) = N ⋅
sin (kL) = 0kL = n ⋅ π , где n = 0, 1, 2, …
n — квантовое число (номер стационарного состояния или его волновой функции)
Слайд 14Вывод: для частицы в ящике стационарными являются не любые состояния,
а только некоторые, выделенные в отношении значений импульса и энергии.
Такие состояния образуют дискретное множество и их можно пронумеровать с помощью поступательного квантового числа n .
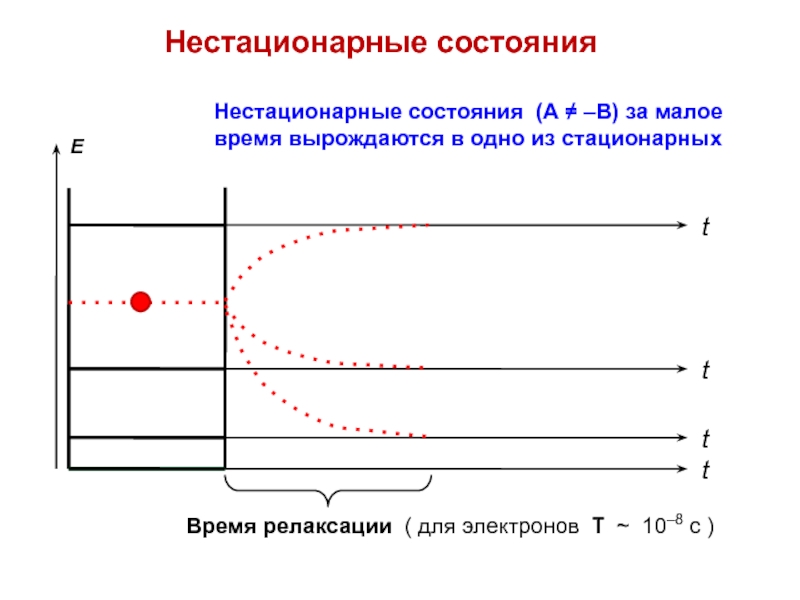
Слайд 15Нестационарные состояния
Нестационарные состояния (А ≠ –В) за малое время вырождаются
в одно из стационарных
![Волновые функцииψ(х) ~ sin[(πn/L)x]](/img/thumbs/5c5dca763e0d3767815c4017c73f79ac-800x.jpg "Частица в ящике Волновые функцииψ(х) ~ sin[(πn/L)x]")
Слайд 17ψ(n = 0) = sin[(π0/L)х] = 0 (для всех х)
n
≠ 0
Минимальная или «нулевая» энергия
Еmin = E1 = π22 /
2mL2 Вероятность обнаружить частицу всюду равна 0. Следовательно, такое состояние не имеет физического смысла (нереализуемо).
![ψ(n = 0) = sin[(π0/L)х] = 0 (для всех х)n ≠ 0Минимальная или «нулевая» энергияЕmin = E1](/img/thumbs/f16cfbf23acfa735c2e6686ca17dd31b-800x.jpg "Частица в ящике ψ(n = 0) = sin[(π0/L)х] = 0 (для всех х)n ≠")
Слайд 19Классический предел
При очень больших значениях n максимумы и минимумы вероятности
становятся неразличимыми
(детекторы дают только усредненную картину)
Слайд 23Плотность уровней Ω ~ L2
В случае макроскопических размеров ящика
расстояния между уровнями становятся настолько малыми, что обнаружить их оказывается
невозможно.Вместо совокупности дискретных уровней образуется сплошная энегетическая зона.
Классический предел по размеру
Слайд 24Влияние размера ящика
Атом: L ≈ 10–10 м
Атомное ядро: L ≈
10–15 м
Электрон не может длительное время
(более чем 10–8 с)
находиться внутри ядра
Слайд 29Трехмерный ящик
Ψ = Ψ(x, y, z) = ψ(x) ⋅ ψ(y)
⋅ ψ(z)
nX = 1, 2, 3, …
nY = 1, 2,
3, …nZ = 1, 2, 3, …
Слайд 32Пространство внутри трехмерного ящика разбивается узловыми плоскостями на ячейки, имеющие
форму параллелепипедов.
Внутри каждой ячейки волновая функция имеет максимальное значение
в центре. По мере приближения к границам ячейки волновая функция спадает до нуля по синусоидальному закону.
При больших значениях квантовых чисел размеры ячеек становятся настолько малыми, что максимумы и минимумы вероятности обнаружения частицы становятся неразличимыми.
Любые детекторы показывают только усредненную картину
P(x, y, z) = const
Классический предел
Слайд 33
Домашнее задание
Задача 4.1.
В трехмерном потенциальном ящике с размерами
LX =
3 нм ; LY = 4 нм ;
LZ = 5 нмнаходится атом 4Не в стационарном состоянии с квантовыми числами ( nX ; nY ; nZ ).
1. Вычислить полную кинетическую энергию атома
Е = ??? (в джоулях).
2. Вычислить модуль вектора импульса
| P | = ??? (в н ⋅ с)
Слайд 34
Задача 4.2.
В трехмерном потенциальном ящике с размерами
LX = 3
нм ; LY = 4 нм ; LZ
= 5 нмнаходится атом 4Не в стационарном состоянии с квантовыми числами ( nX ; nY ; nZ ).
Вычислить работу (в джоулях), необходимую для адиабатического разделения ящика на две равные части перегородкой, перпендикулярной:
а) оси X; б) оси Y; в) оси Z
Слайд 35
Задача 4.3.
В трехмерном потенциальном ящике с размерами
LX = 3
нм ; LY = 4 нм ; LZ
= 5 нмнаходится атом 4Не в стационарном состоянии с квантовыми числами ( nX ; nY ; nZ ).
Изобразить узловую структуру волновой функции
