Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Числовые характеристики выборки
Содержание
- 1. Числовые характеристики выборки
- 2. Структура лекции Числовые характеристики выборки: средняя, медиана, модаОписательные статистикиКейс «Надо ли увольнять сотрудника?»
- 3. Начальная обработка статистических данных Вычисление средних: среднее
- 4. Какую из средних следует использовать?После начальной обработки
- 5. Какую из средних следует использовать? 28После начальной
- 6. Описательная статистикаСреднее значениеСтандартная ошибкаМедианаСтандартное отклонение и дисперсияЭксцессАссиметричностьСтандартная (средняя квадратическая) ошибка ассиметрииСтандартная ошибка эксцесса
- 7. Стандартное отклонениеДля определения диапазонов попадания определенной доли
- 8. Степенные средние Мода и медиана – структурные позиционные
- 9. Скачать презентанцию
Структура лекции Числовые характеристики выборки: средняя, медиана, модаОписательные статистикиКейс «Надо ли увольнять сотрудника?»
Слайды и текст этой презентации
Слайд 2Структура лекции
Числовые характеристики выборки: средняя, медиана, мода
Описательные статистики
Кейс «Надо
ли увольнять сотрудника?»
Слайд 3Начальная обработка статистических данных
Вычисление средних: среднее мода, медиана
Мода —
это средняя величина, получаемая путем установления наиболее часто встречающегося значения
в наборе данных. Сколько значений выбрать в качестве моды – решает аналитик.Медиана — это такое значение исследуемой величины, слева и справа от которого находится одинаковое число упорядоченных по возрастанию или убыванию выборочных данных.
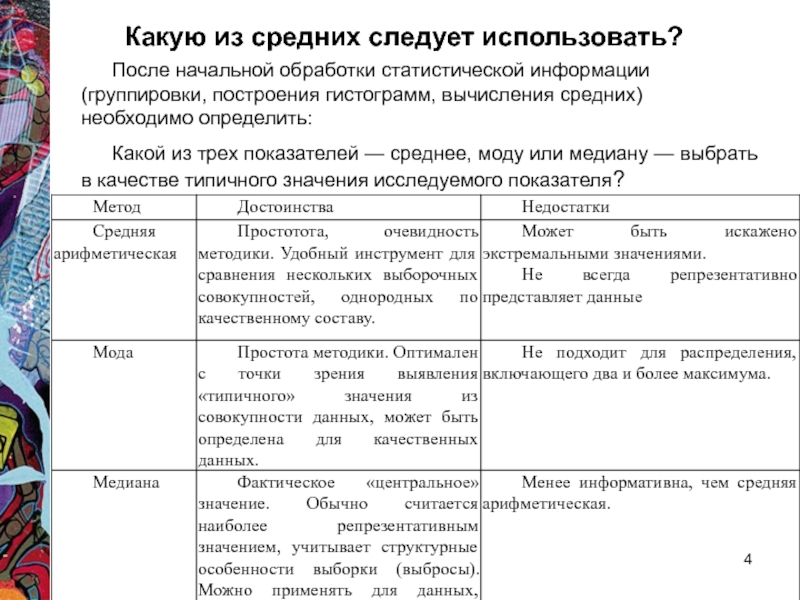
Слайд 4Какую из средних следует использовать?
После начальной обработки статистической информации (группировки,
построения гистограмм, вычисления средних) необходимо определить:
Какой из трех показателей —
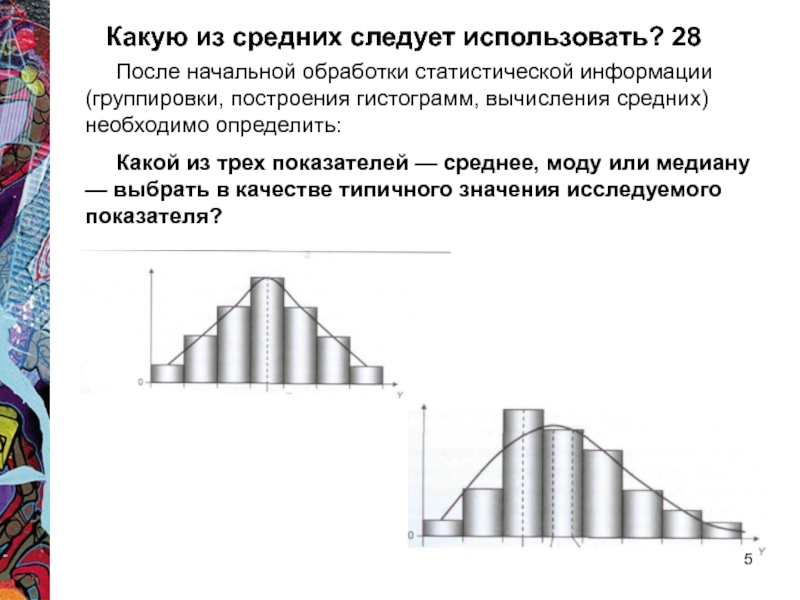
среднее, моду или медиану — выбрать в качестве типичного значения исследуемого показателя?Слайд 5Какую из средних следует использовать? 28
После начальной обработки статистической информации
(группировки, построения гистограмм, вычисления средних) необходимо определить:
Какой из трех показателей
— среднее, моду или медиану — выбрать в качестве типичного значения исследуемого показателя?Слайд 6Описательная статистика
Среднее значение
Стандартная ошибка
Медиана
Стандартное отклонение и дисперсия
Эксцесс
Ассиметричность
Стандартная (средняя квадратическая) ошибка
ассиметрии
Стандартная ошибка эксцесса
Слайд 7Стандартное отклонение
Для определения диапазонов попадания определенной доли возможных значений исследуемых
случайных величин
Неравенство Чебышева (для любых совокупностей независимо от законов распределения):
Доля
значений, попадающих в интервал , будет по крайней мере не менее чем .
Доля выступает в качестве оценки вероятности того, что С.В. будет находиться в некотором диапазоне значений.
Слайд 8Степенные средние
Мода и медиана – структурные позиционные средние.
Средняя арифметическая –
степенная средняя.
Общая формула степенной средней:
При k= -1 получим среднюю гармоническую
величину;При k=0 – среднюю геометрическую (используют при измерении средних темпов прироста);
При k=1 –среднюю арифметическую;
При k=2 – среднюю квадратическую и т.д.