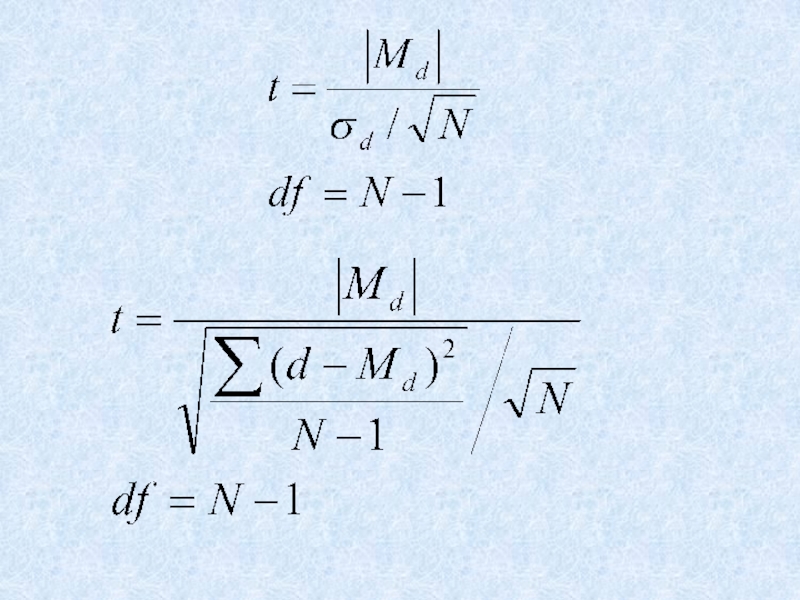Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Критерии различий
Содержание
- 1. Критерии различий
- 2. Критерий t-Стьюдента для зависимых выборокСтатистические гипотезы:H0: M1
- 3. Альтернатива: непараметрический критерий Т-Вилкоксона.Единица анализа – разность (сдвиг) значений признака для каждой пары наблюдений.
- 4. Слайд 4
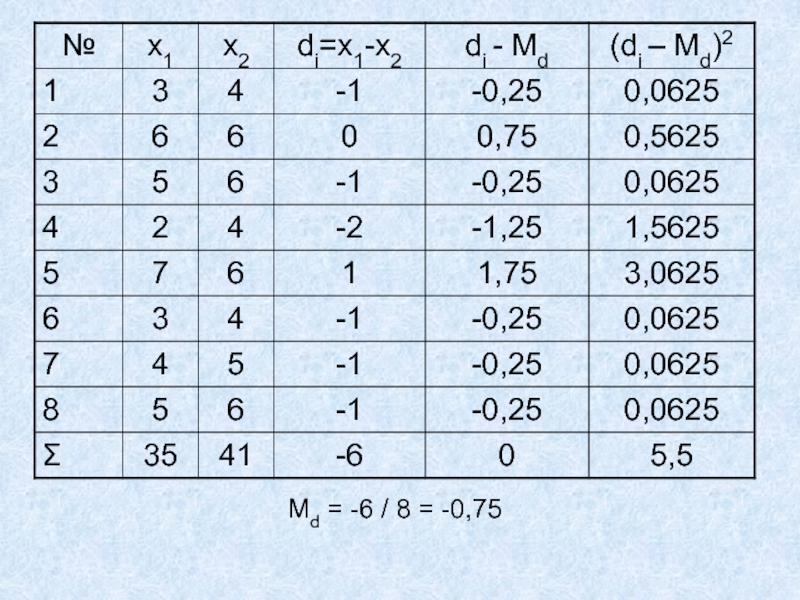
- 5. Мd = -6 / 8 = -0,75
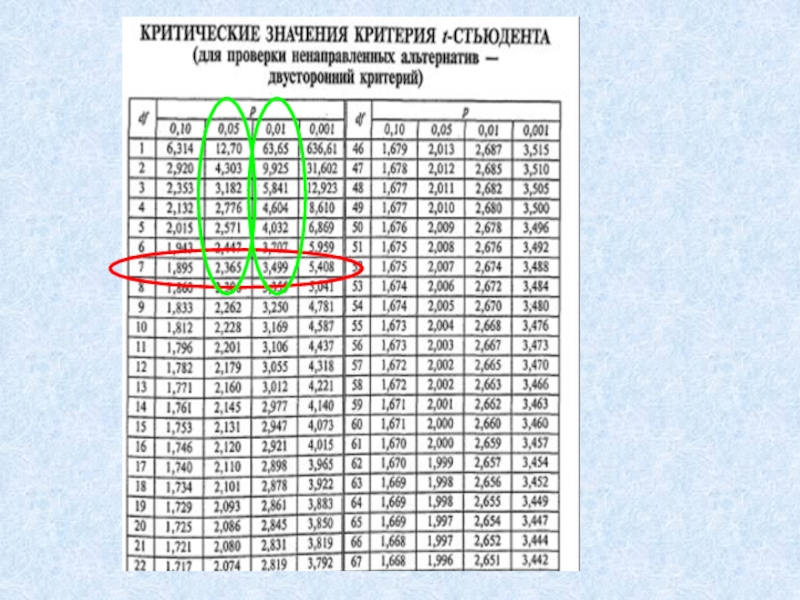
- 6. Слайд 6
- 7. Слайд 7
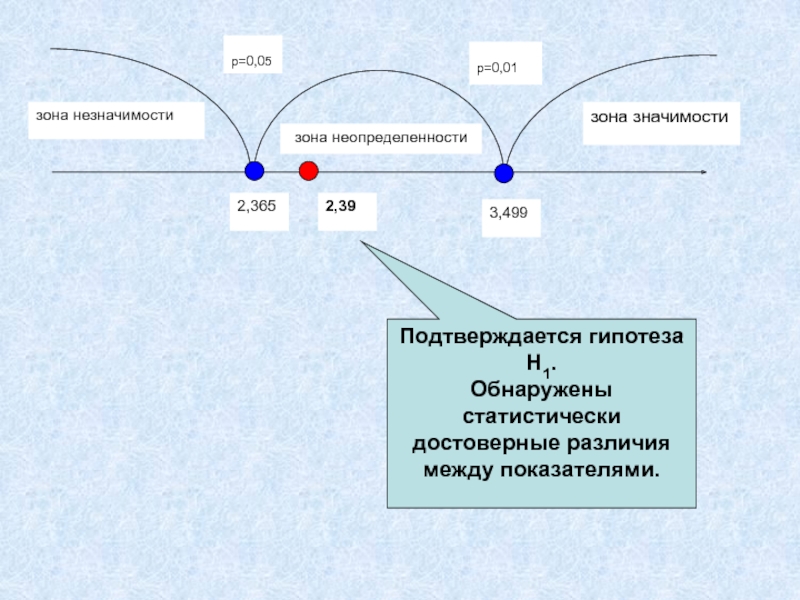
- 8. зона значимостизона незначимостизона неопределенностиp=0,05p=0,012,3653,499Подтверждается гипотеза H1.Обнаружены статистически достоверные различия между показателями.2,39
- 9. Критерий T-ВилкоксонаКритерий является непараметрическим.Параметрический аналог – t-Стьюдента для зависимых выборок.Формулы нет.
- 10. Критерий-исключение, как UЧем меньше эмпирическое значение Т, тем больше различияp=0,05p=0,01зона неопределенностизона незначимостизона значимости
- 11. Слайд 11
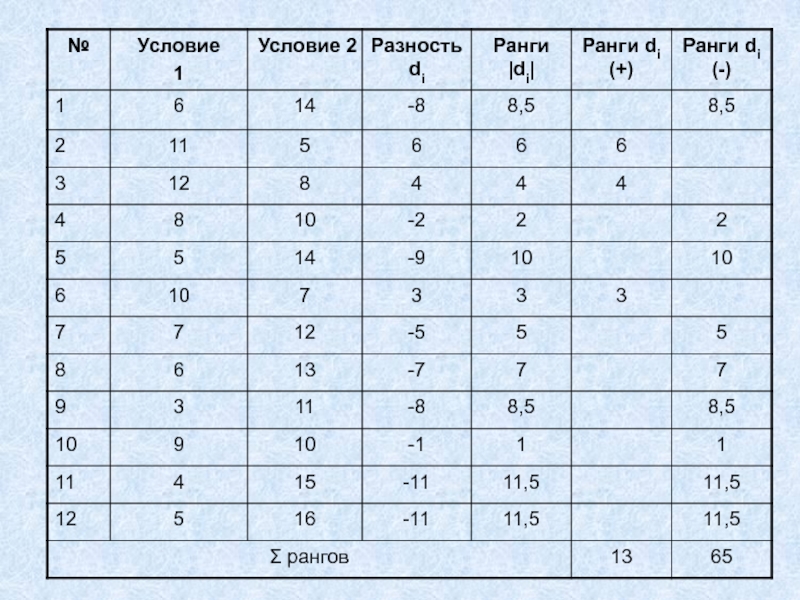
- 12. Последовательность действий:1. Подсчитать разности значений для каждого
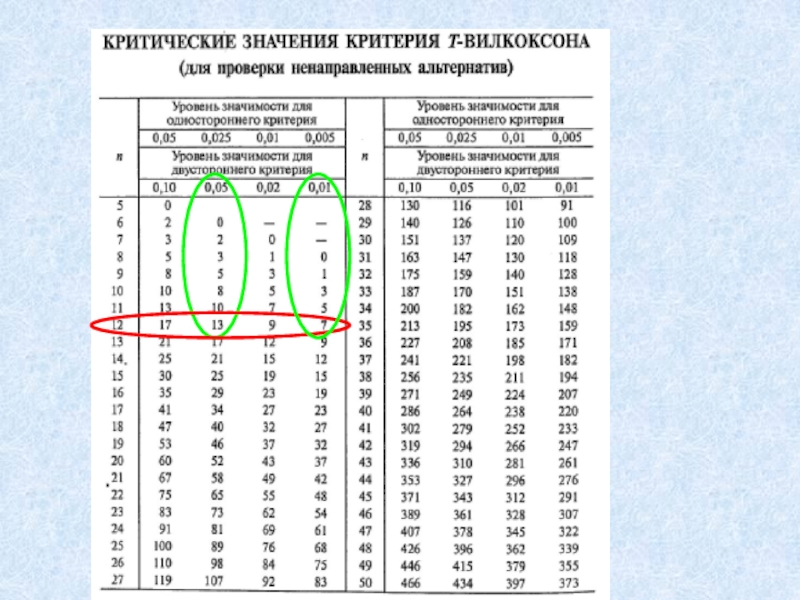
- 13. 5. Определяется p-уровень значимости: Т эмп. сравнивается
- 14. В данном примере:Т1 = 13Т2 = 65Т
- 15. Слайд 15
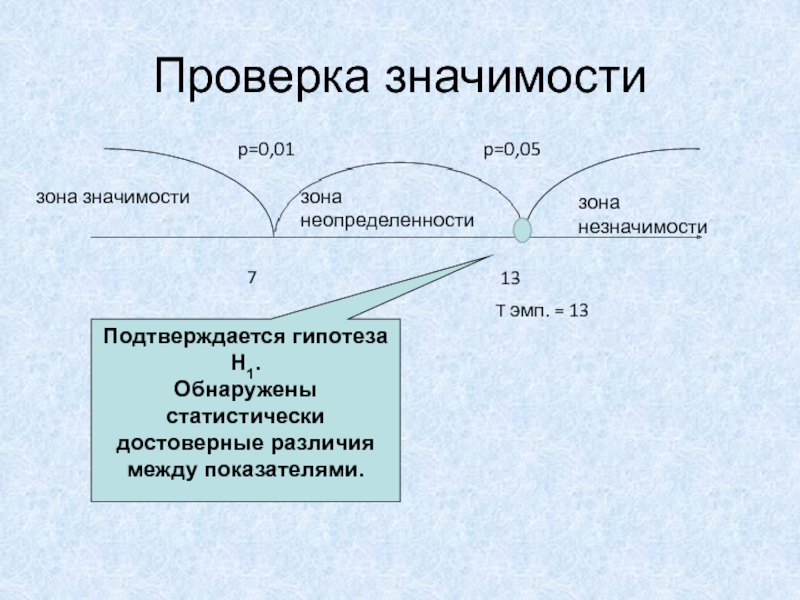
- 16. Проверка значимостиp=0,05p=0,01зона неопределенностизона незначимости7 13T эмп. = 13зона значимостиПодтверждается гипотеза H1.Обнаружены статистически достоверные различия между показателями.
- 17. Скачать презентанцию
Критерий t-Стьюдента для зависимых выборокСтатистические гипотезы:H0: M1 = M2H1: M1 ≠ M2Условия использования:выборки являются зависимыми;распределение признака в обеих выборках соответствует нормальному закону.
Слайды и текст этой презентации
Слайд 2Критерий t-Стьюдента для зависимых выборок
Статистические гипотезы:
H0: M1 = M2
H1: M1
≠ M2
нормальному закону.
Слайд 3Альтернатива: непараметрический критерий Т-Вилкоксона.
Единица анализа – разность (сдвиг) значений признака
для каждой пары наблюдений.
Слайд 8зона значимости
зона незначимости
зона неопределенности
p=0,05
p=0,01
2,365
3,499
Подтверждается гипотеза H1.
Обнаружены статистически достоверные различия между
показателями.
2,39
Слайд 9Критерий T-Вилкоксона
Критерий является непараметрическим.
Параметрический аналог – t-Стьюдента для зависимых выборок.
Формулы
нет.
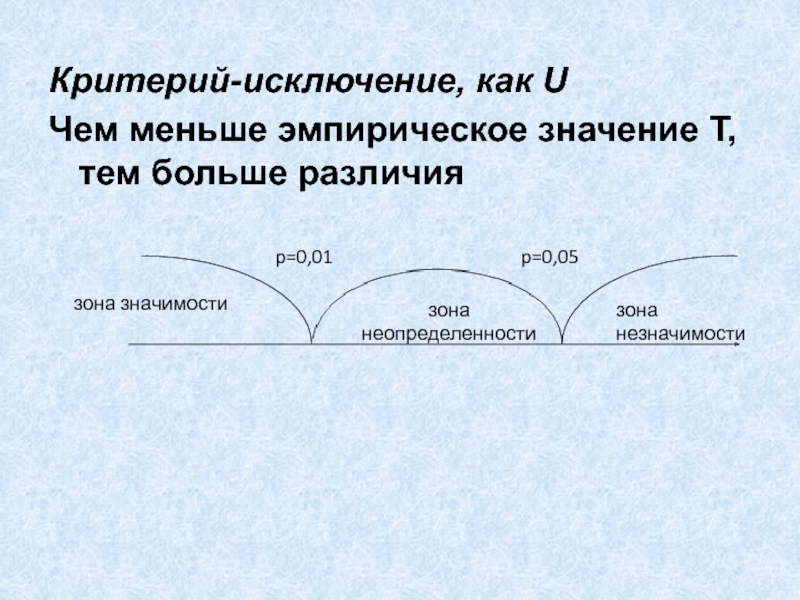
Слайд 10Критерий-исключение, как U
Чем меньше эмпирическое значение Т, тем больше различия
p=0,05
p=0,01
зона
неопределенности
зона незначимости
зона значимости
Слайд 12Последовательность действий:
1. Подсчитать разности значений для каждого объекта выборки.
2. Ранжировать
абсолютные значения разностей.
3. Выписать ранги положительных и отрицательных разностей.
4. Подсчитать
суммы рангов отдельно для положительных и отрицательных разностей. За эмпирическое значение Т принимается меньшая сумма.
Слайд 135. Определяется p-уровень значимости: Т эмп. сравнивается с Т кр.
по таблице критических значений (для соответствующего объема выборки).
Различия достоверны, если
Т эмп. ≤ Т кр.6. Принимается статистическое решение и формулируется вывод.
Слайд 14В данном примере:
Т1 = 13
Т2 = 65
Т эмп. = 13
По
таблице критических значений определяем уровень значимости.
Т эмп. = Т кр.
принимается гипотеза Н1 о достоверности различий.
Слайд 16Проверка значимости
p=0,05
p=0,01
зона неопределенности
зона незначимости
7
13
T эмп. = 13
зона значимости
Подтверждается гипотеза
H1.
Обнаружены статистически достоверные различия между показателями.
