ожидания нормально распределенной случайной величины:
а) при известном
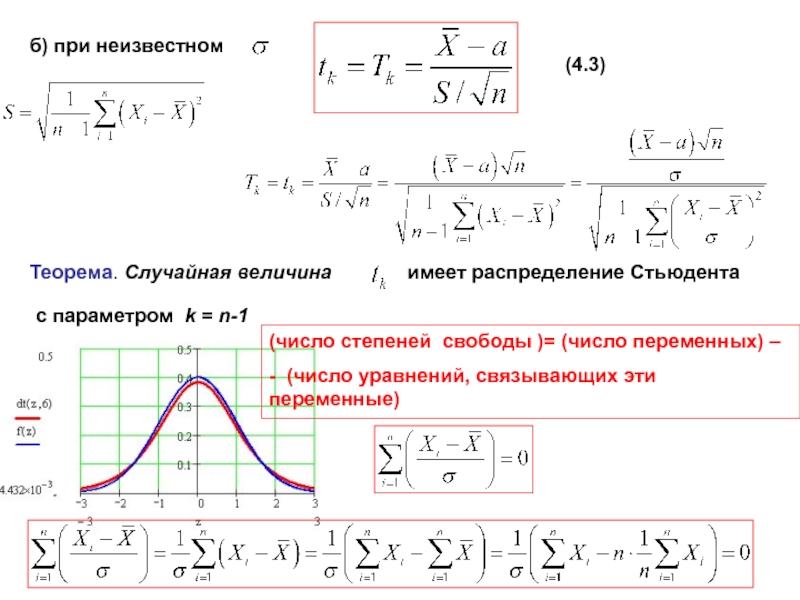
б) при неизвестном
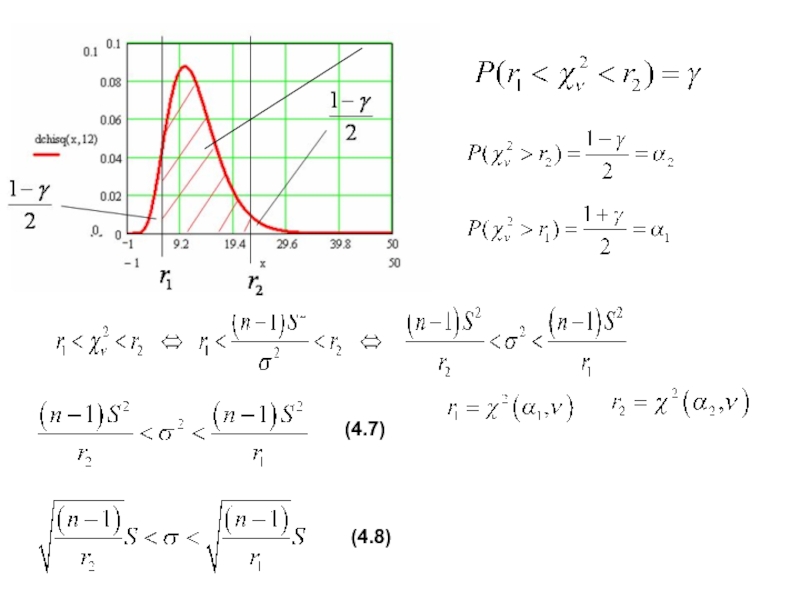
3. Построение
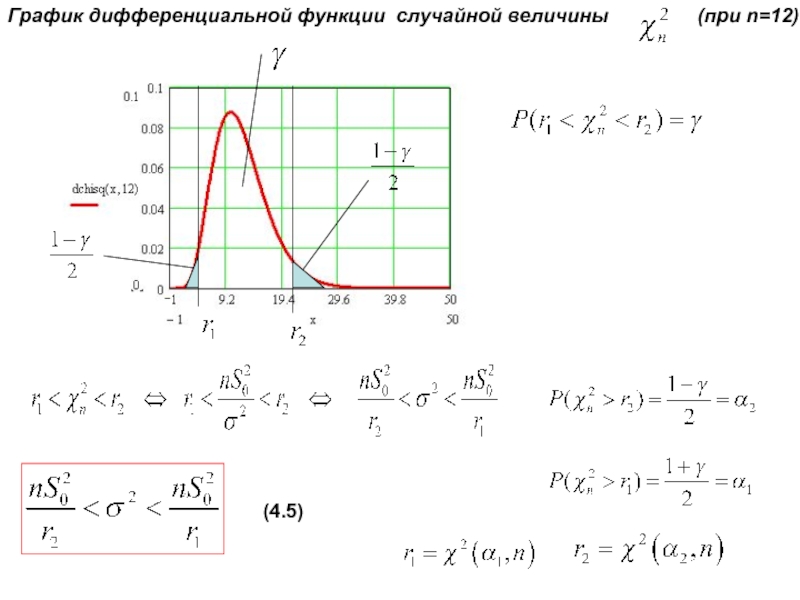
доверительного интервала для дисперсии нормально распределенной случайной величины:а) при известном
б) при неизвестном
1. Доверительные интервалы и доверительные вероятности
Пусть
- исследуемый признак
- случайная выборка
- неизвестный параметр
- случайные величины (статистики)