Слайд 1Лекция 5
Тесты проверки предпосылок теоремы Гаусса-Маркова
Слайд 2Методика проверки статистических гипотез
Определение. Под статистической гипотезой понимается любое предположение
о виде закона распределения случайной величины или значениях его параметров.
Примеры
статистических гипотез:
Н0:(U имеет нормальный закон распределения).
H0:(параметр а0=0)
Н1:(параметр а0=1)
Гипотезы H0 и H1 называются основной и альтернативной.
Слайд 3Методика проверки статистических гипотез
Алгоритм проверки статистических гипотез.
Формулируется статистическая гипотеза H0.
Искусственно
формируется случайная величина «Z», закон распределения которой известен [Pz(t,a1, a2)],
котoрая тесно связана с гипотезой.
Область допустимых значений Z делится на две части: Ω0 в которой гипотеза принимается и, Ω в которой она отклоняется. Граница этих областей определяется из условия, что Z попадает в область Ω0 с заданной вероятностью «р».
По данным выборки вычисляется значение случайной величины Z и проверяется ее принадлежность область Ω0.
Слайд 4Методика проверки статистических гипотез
Возможные ошибки при проверке статистических гипотез.
Ошибка первого
рода.
Когда справедливая гипотеза отклоняется.
Ошибка второго рода.
Когда ложная гипотеза принимается.
Слайд 5
Модель: Y = b1 + b2X + u
Нулевая гипотеза:
Альтернативная гипотеза:
ПРОВЕРКА ГИПОТЕЗ
СВЯЗАННЫХ С КОЭФФИЦИЕНТАМИ РЕГРЕССИИ
Проверка нулевой гипотезы, что 2 = 20
или альтернативной гипотезы.
Слайд 6 Модель: Y = b1 + b2X + u
Нулевая гипотеза:
Альтернативная гипотеза:
Пример модели: Темпы общей инфляции в
зависимости
от темпов роста заработной платы.
p = b1 + b2w + u
Нулевая гипотеза:
Альтернативная гипотеза:
4
ПРОВЕРКА ГИПОТЕЗ
СВЯЗАННЫХ С КОЭФФИЦИЕНТАМИ РЕГРЕССИИ
Слайд 7
6
ПРОВЕРКА ГИПОТЕЗ
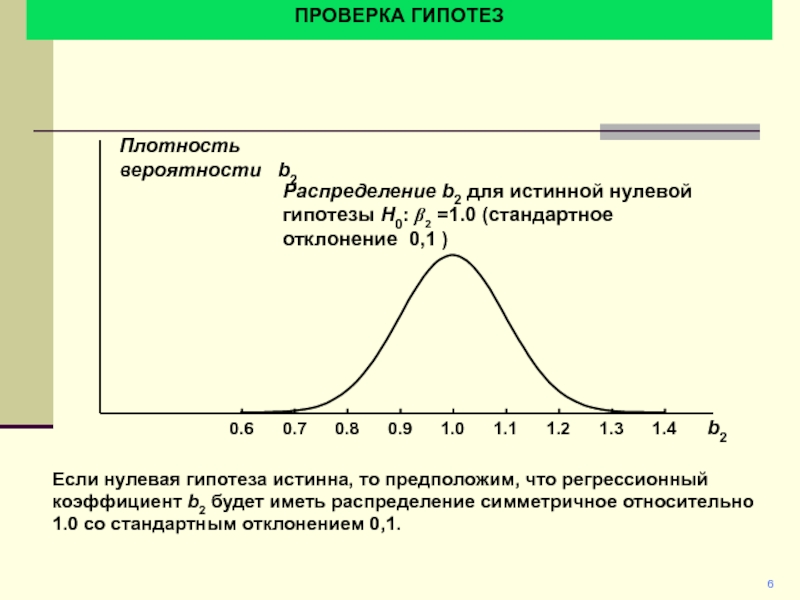
Плотность вероятности b2
Распределение b2 для истинной нулевой гипотезы
H0: b2 =1.0 (стандартное отклонение 0,1 )
b2
1.0
1.1
0.9
0.8
0.7
0.6
1.2
1.3
1.4
Если нулевая гипотеза истинна,
то предположим, что регрессионный коэффициент b2 будет иметь распределение симметричное относительно 1.0 со стандартным отклонением 0,1.
Слайд 8
6
ПРОВЕРКА ГИПОТЕЗ
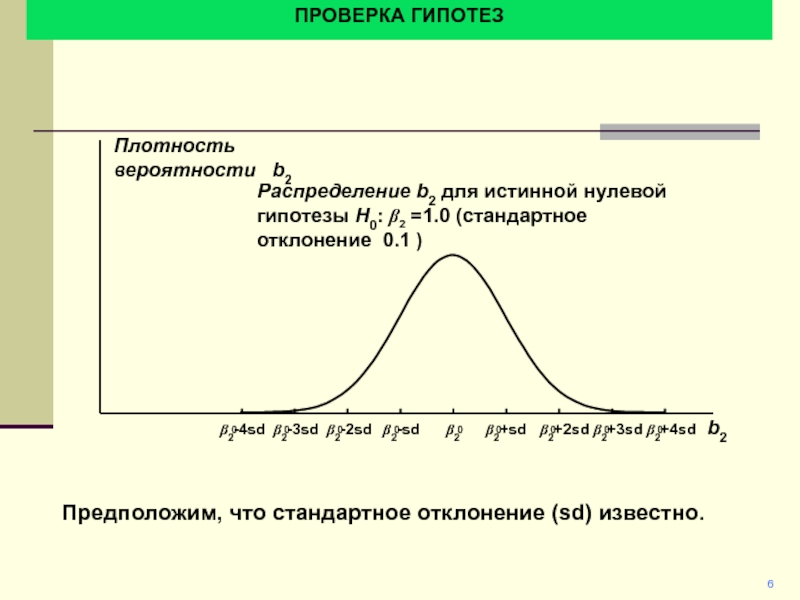
Плотность вероятности b2
Распределение b2 для истинной нулевой гипотезы
H0: b2 =1.0 (стандартное отклонение 0.1 )
b2
Предположим, что стандартное отклонение
(sd) известно.
Слайд 9
9
ПРОВЕРКА ГИПОТЕЗ
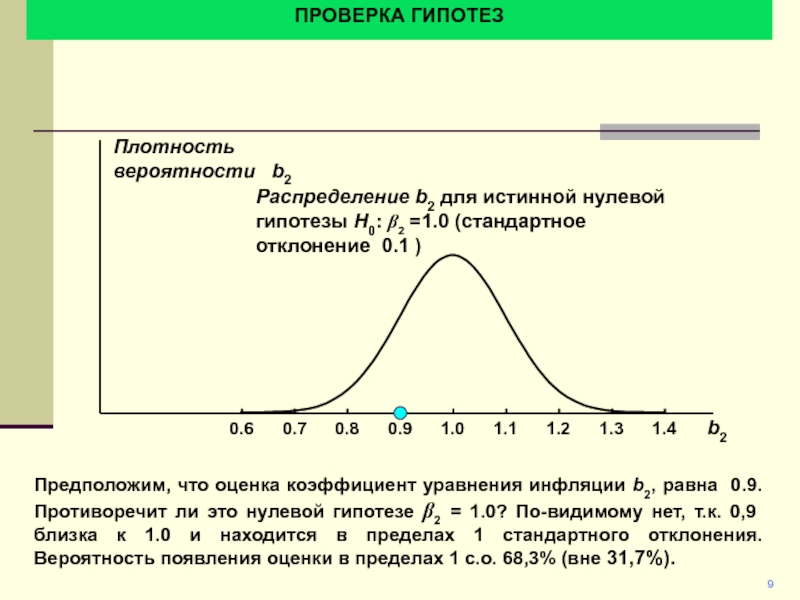
Предположим, что оценка коэффициент уравнения инфляции b2, равна 0.9.
Противоречит ли это нулевой гипотезе b2 = 1.0? По-видимому нет,
т.к. 0,9 близка к 1.0 и находится в пределах 1 стандартного отклонения. Вероятность появления оценки в пределах 1 с.о. 68,3% (вне 31,7%).
1.0
1.1
0.9
0.8
0.7
0.6
1.2
1.3
1.4
b2
Плотность вероятности b2
Распределение b2 для истинной нулевой гипотезы H0: b2 =1.0 (стандартное отклонение 0.1 )
Слайд 10
14
ПРОВЕРКА ГИПОТЕЗ
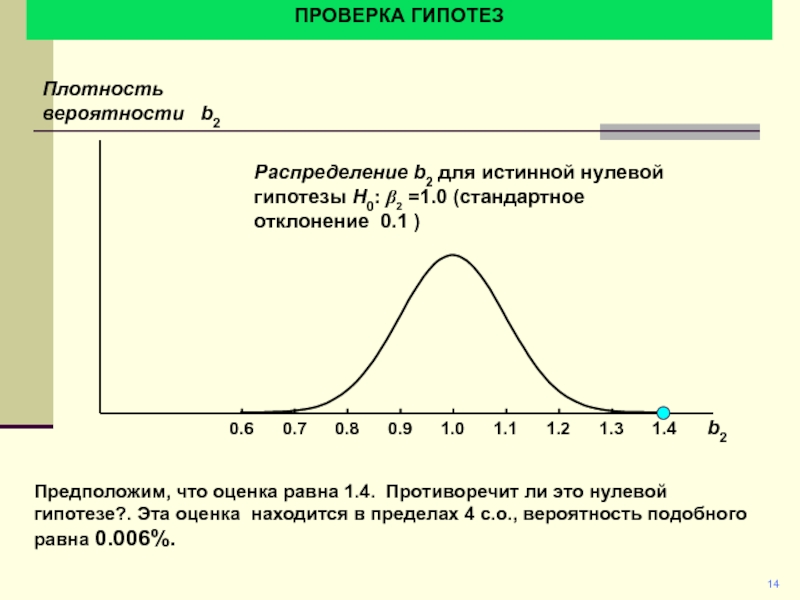
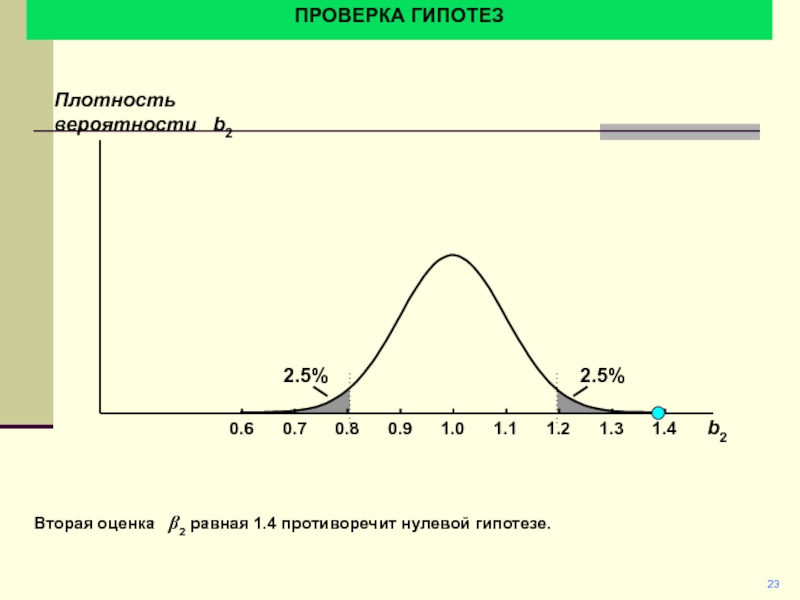
Предположим, что оценка равна 1.4. Противоречит ли это нулевой
гипотезе?. Эта оценка находится в пределах 4 с.о., вероятность подобного
равна 0.006%.
1.0
1.1
0.9
0.8
0.7
0.6
1.2
1.3
1.4
b2
Плотность вероятности b2
Распределение b2 для истинной нулевой гипотезы H0: b2 =1.0 (стандартное отклонение 0.1 )
Слайд 11
14
ПРОВЕРКА ГИПОТЕЗ
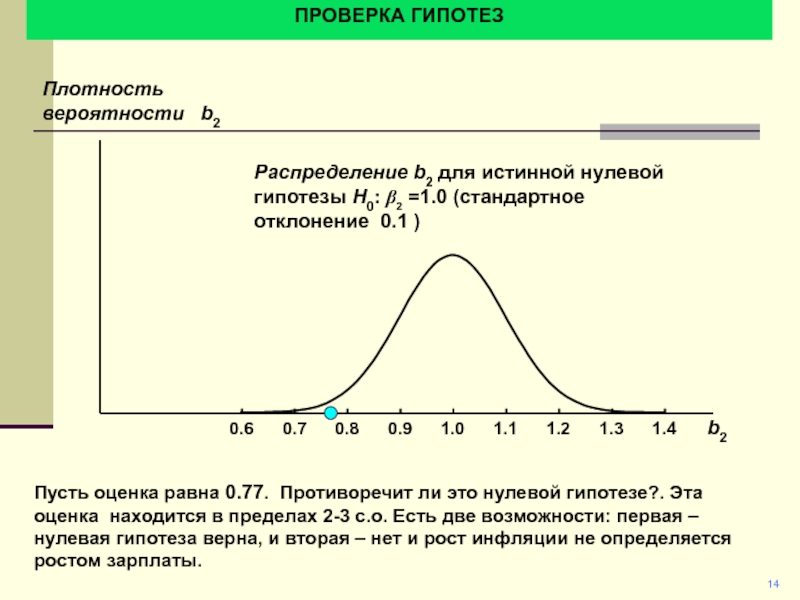
Пусть оценка равна 0.77. Противоречит ли это нулевой гипотезе?.
Эта оценка находится в пределах 2-3 с.о. Есть две возможности:
первая – нулевая гипотеза верна, и вторая – нет и рост инфляции не определяется ростом зарплаты.
1.0
1.1
0.9
0.8
0.7
0.6
1.2
1.3
1.4
b2
Плотность вероятности b2
Распределение b2 для истинной нулевой гипотезы H0: b2 =1.0 (стандартное отклонение 0.1 )
Слайд 12
6
ПРОВЕРКА ГИПОТЕЗ
Плотность вероятности b2
Распределение b2 для истинной нулевой гипотезы
H0: b2 =1.0 (стандартное отклонение 0.1 )
b2
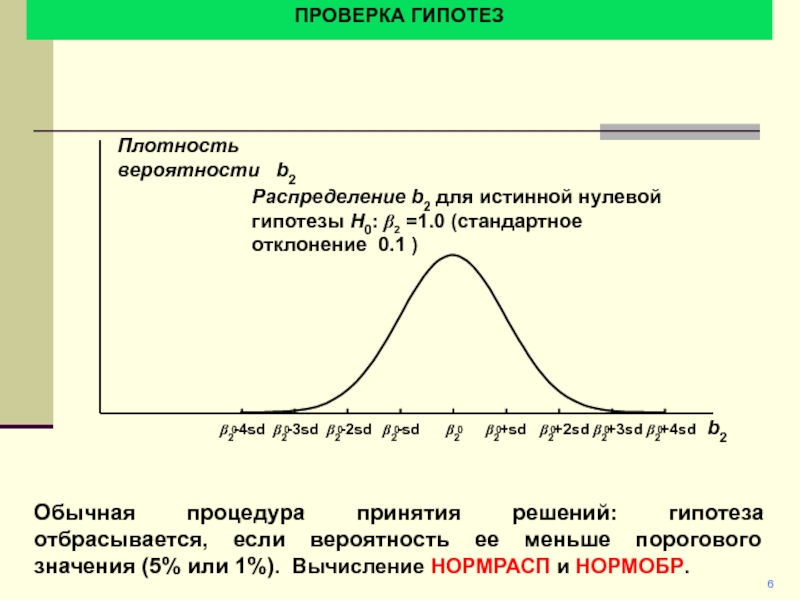
Обычная процедура принятия решений:
гипотеза отбрасывается, если вероятность ее меньше порогового значения (5% или 1%). Вычисление НОРМРАСП и НОРМОБР.
Слайд 13
21
ПРОВЕРКА ГИПОТЕЗ
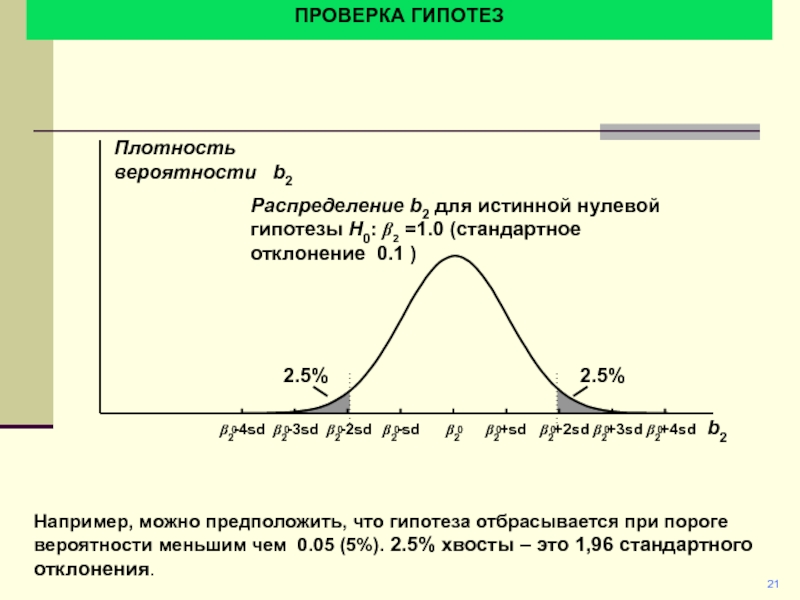
Например, можно предположить, что гипотеза отбрасывается при пороге вероятности
меньшим чем 0.05 (5%). 2.5% хвосты – это 1,96 стандартного
отклонения.
2.5%
2.5%
b2
Плотность вероятности b2
Распределение b2 для истинной нулевой гипотезы H0: b2 =1.0 (стандартное отклонение 0.1 )
Слайд 142.5%
2.5%
23
ПРОВЕРКА ГИПОТЕЗ
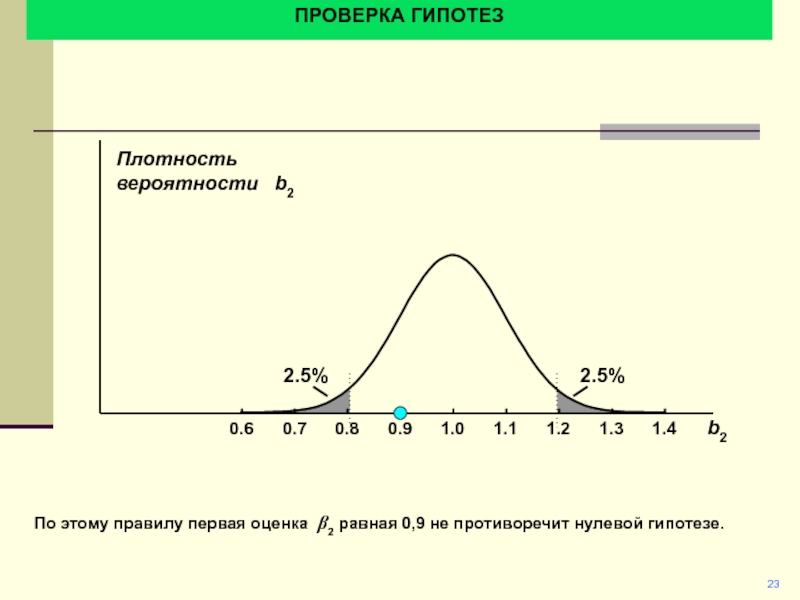
По этому правилу первая оценка b2 равная 0,9
не противоречит нулевой гипотезе.
1.0
1.1
0.9
0.8
0.7
0.6
1.2
1.3
1.4
b2
Плотность вероятности b2
Слайд 152.5%
2.5%
23
ПРОВЕРКА ГИПОТЕЗ
Вторая оценка b2 равная 1.4 противоречит нулевой
гипотезе.
1.0
1.1
0.9
0.8
0.7
0.6
1.2
1.3
1.4
b2
Плотность вероятности b2
Слайд 162.5%
2.5%
23
ПРОВЕРКА ГИПОТЕЗ
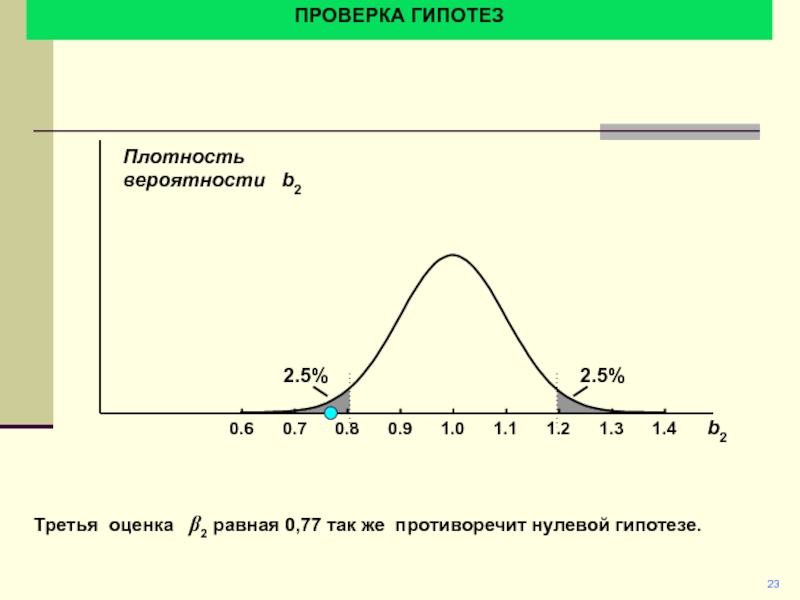
Третья оценка b2 равная 0,77 так же
противоречит нулевой гипотезе.
1.0
1.1
0.9
0.8
0.7
0.6
1.2
1.3
1.4
b2
Плотность вероятности b2
Слайд 17
ПРОВЕРКА ГИПОТЕЗ
2.5%
2.5%
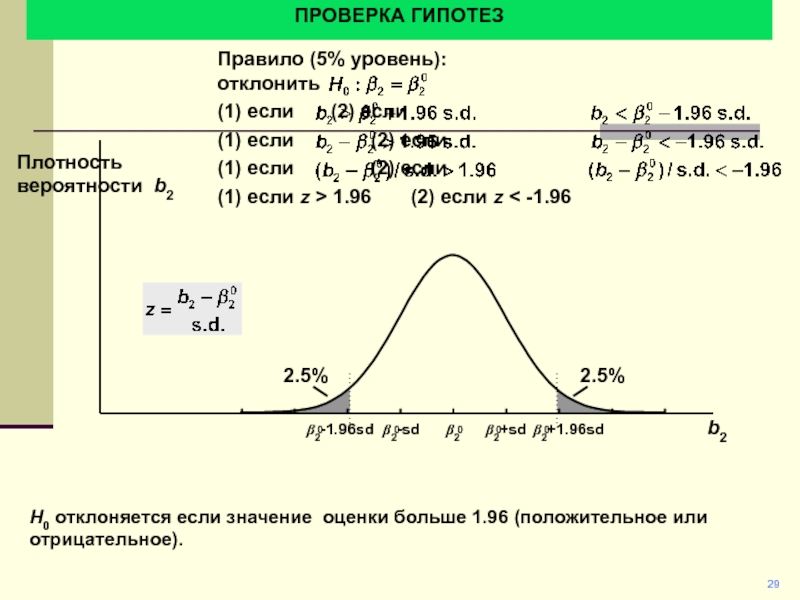
Правило (5% уровень):
отклонить
(1) если (2) если
(1)
если (2) если
(1) если
(2) если
(1) если z > 1.96 (2) если z < -1.96
Плотность вероятности b2
b2
H0 отклоняется если значение оценки больше 1.96 (положительное или отрицательное).
29
Слайд 18
ПРОВЕРКА ГИПОТЕЗ
2.5%
2.5%
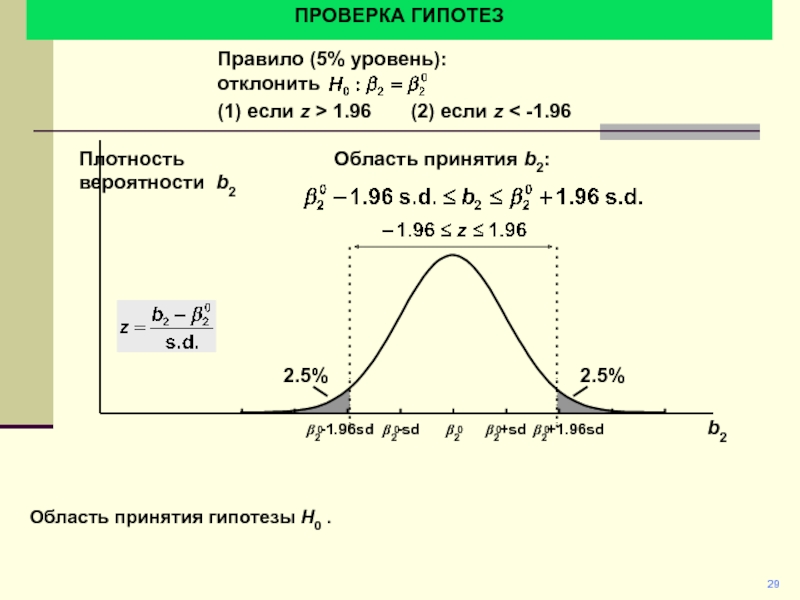
Правило (5% уровень):
отклонить
(1) если z > 1.96
(2) если z < -1.96
Плотность вероятности b2
b2
Область принятия гипотезы
H0 .
29
Область принятия b2:
Слайд 192.5%
2.5%
36
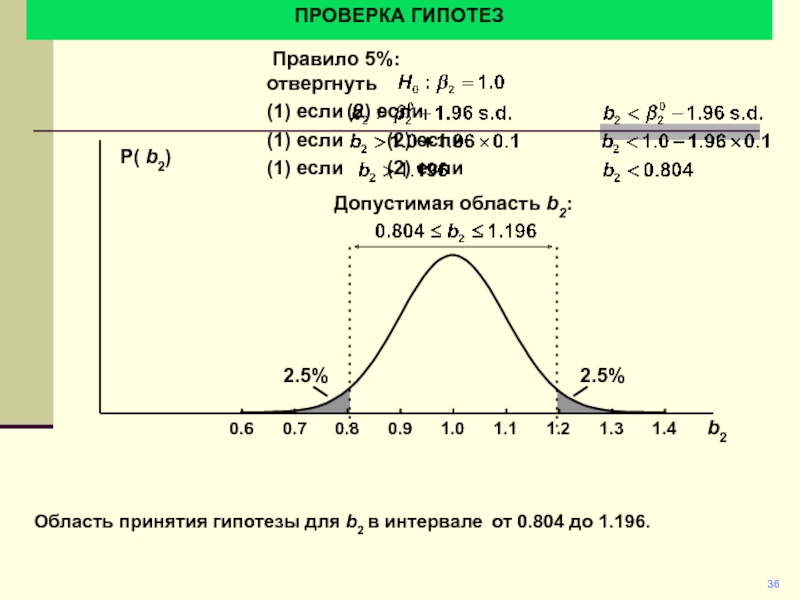
ПРОВЕРКА ГИПОТЕЗ
Область принятия гипотезы для b2 в интервале от 0.804
до 1.196.
1.0
1.1
0.9
0.8
0.7
0.6
1.2
1.3
1.4
Р( b2)
b2
Правило 5%:
отвергнуть
(1) если (2) если
(1) если
(2) если
(1) если (2) если
Допустимая область b2:
Слайд 20
37
ПРОВЕРКА ГИПОТЕЗ
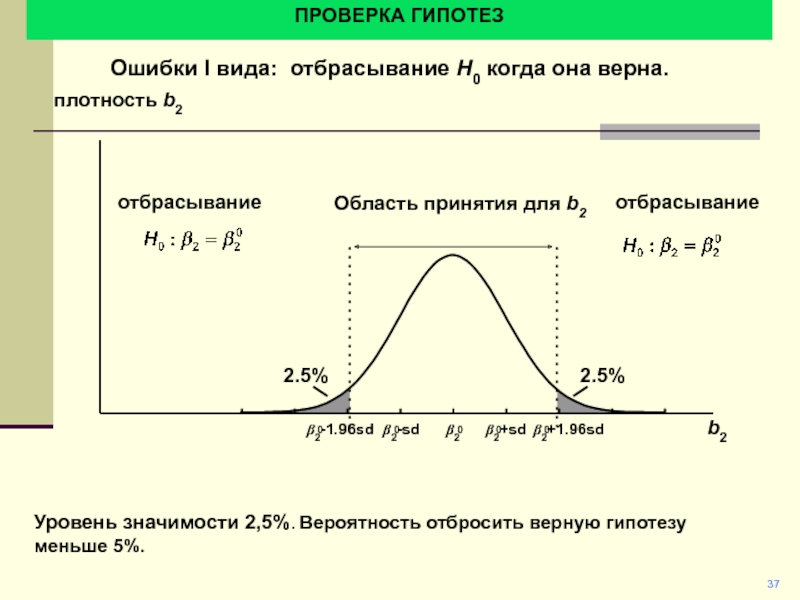
Уровень значимости 2,5%. Вероятность отбросить верную гипотезу меньше 5%.
2.5%
2.5%
Ошибки I вида: отбрасывание H0 когда она верна.
отбрасывание
отбрасывание
плотность b2
b2
Область
принятия для b2
Слайд 21
42
ПРОВЕРКА ГИПОТЕЗ
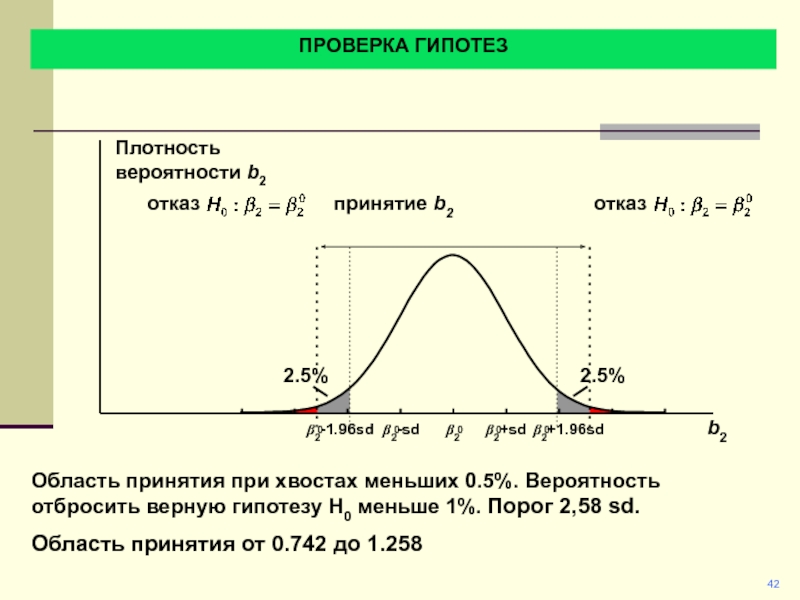
Область принятия при хвостах меньших 0.5%. Вероятность отбросить
верную гипотезу H0 меньше 1%. Порог 2,58 sd.
Область принятия
от 0.742 до 1.258
2.5%
2.5%
Плотность вероятности b2
b2
отказ
принятие b2
отказ
Слайд 22
47
ПРОВЕРКА ГИПОТЕЗ
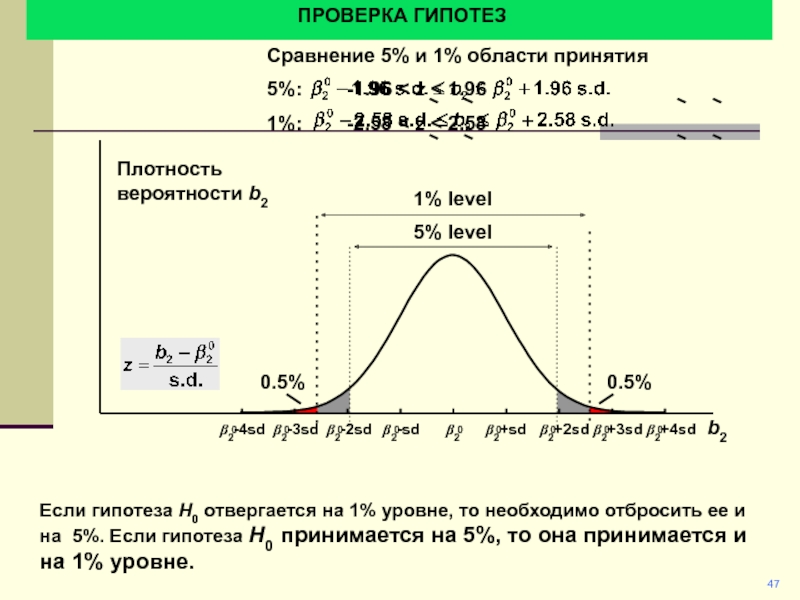
Если гипотеза H0 отвергается на 1% уровне,
то необходимо отбросить ее и на 5%. Если гипотеза H0
принимается на 5%, то она принимается и на 1% уровне.
0.5%
0.5%
Сравнение 5% и 1% области принятия
5%: -1.96 < z < 1.96
1%: -2.58 < z < 2.58
5% level
1% level
Плотность вероятности b2
b2
Слайд 23ПРОВЕРКА ГИПОТЕЗ
Принятие решений на 5% и 1% уровне.
49
Отказ H0 на1%
ур. (и на 5% уровне)
Отказ H0 на 5% ур. Но
не на 1% ур.
Отказ H0 на 5% ур-не но не на 1% ур.
Отказ H0 на 1% уровне (и на 5% ур-не)
Принятие H0 на 5% ур. (или на 1% ур.)
1.000
0.804
0.742
1.196
1.258
Инфляция/
зарплата
Общий случай
Решение
Слайд 24b2
b2+sd
b2+2.58sd
b2-sd
b2-2.58sd
0.5%
0.5%
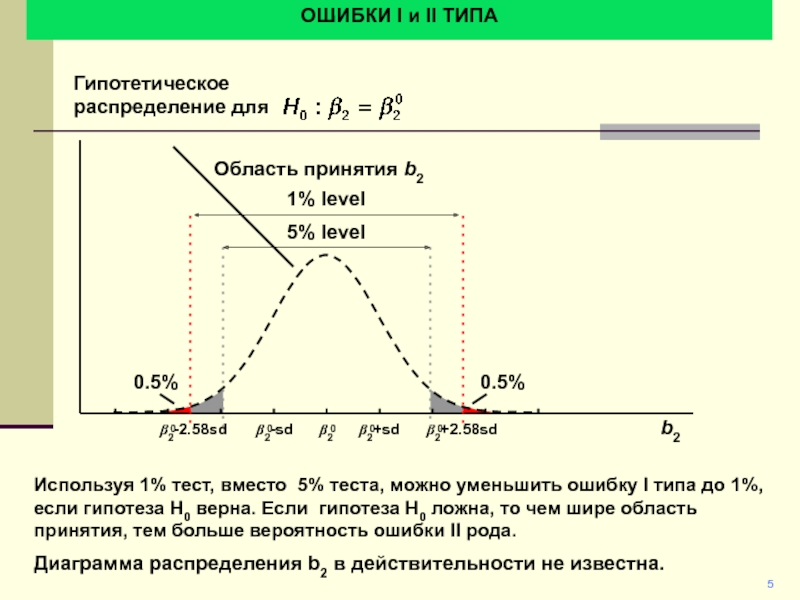
ОШИБКИ I и II ТИПА
5% level
1% level
Гипотетическое распределение для
Область
принятия b2
0
0
0
0
0
Используя 1% тест, вместо 5% теста, можно уменьшить ошибку
I типа до 1%, если гипотеза H0 верна. Если гипотеза H0 ложна, то чем шире область принятия, тем больше вероятность ошибки II рода.
Диаграмма распределения b2 в действительности не известна.
5
b2
Слайд 25
F –КРИТЕРИЙ КАЧЕСТВА ОЦЕНИВАНИЯ
R2 – мера качества объяснения регрессионным уравнением
закономерности. Нулевая гипотеза для тестирования заключается в том, что модель
не имеет объяснительной силы.
4
Слайд 26
9
Для оценки качества R2 можно использовать F – статистику (распределение
Фишера). k- число степеней свободы (количество объясняющих переменных и свободный
коэффициент), n - число экспериментов.
F –КРИТЕРИЙ КАЧЕСТВА ОЦЕНИВАНИЯ
Слайд 27
F –КРИТЕРИЙ КАЧЕСТВА ОЦЕНИВАНИЯ
Легко показать, что RSS/TSS равно 1
- R2. F монотонная функция R2. С увеличением R2 F
увеличивается
10
Слайд 28
12
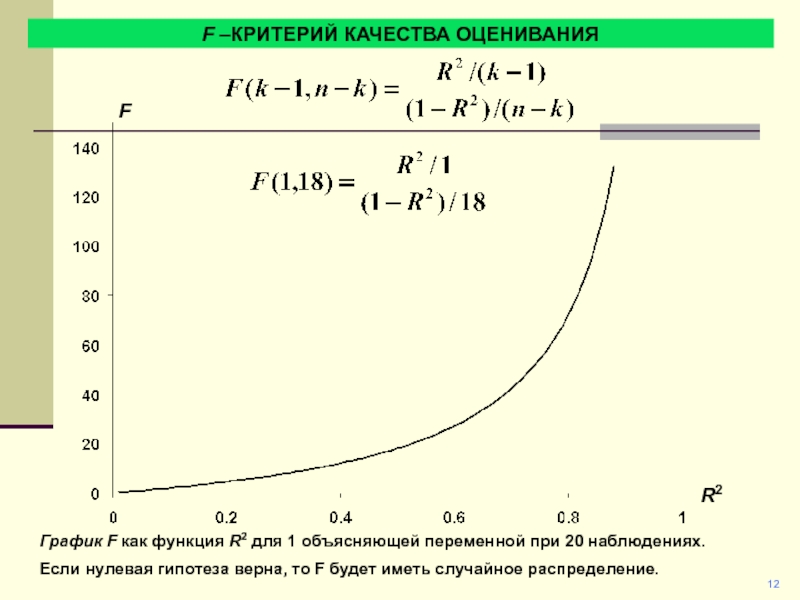
F –КРИТЕРИЙ КАЧЕСТВА ОЦЕНИВАНИЯ
R2
F
График F как функция R2 для
1 объясняющей переменной при 20 наблюдениях.
Если нулевая гипотеза верна,
то F будет иметь случайное распределение.
Слайд 2932
F –КРИТЕРИЙ КАЧЕСТВА ОЦЕНИВАНИЯ
Слайд 30
F –КРИТЕРИЙ КАЧЕСТВА ОЦЕНИВАНИЯ
34
Слайд 31ТесТ
ГолдФелда-квандта
Лекция 5. Часть 2
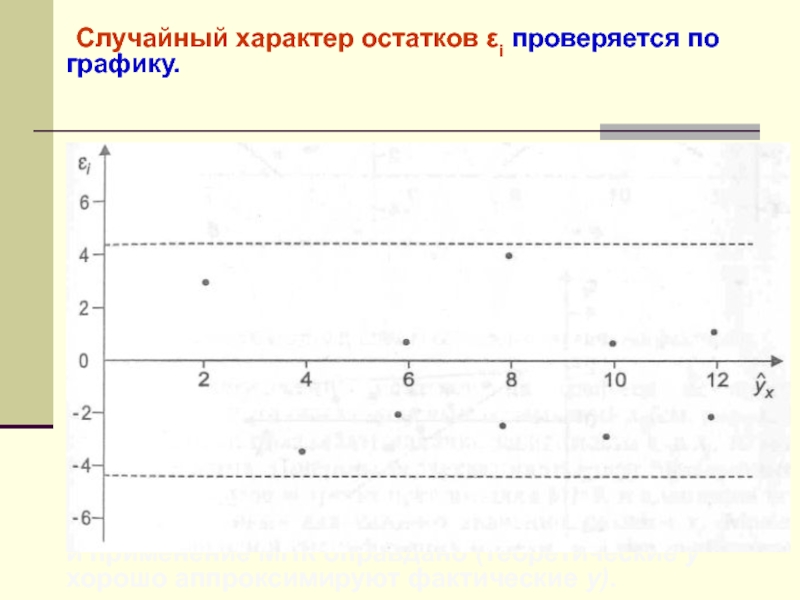
Слайд 32 Случайный характер остатков εi проверяется по графику.
Если
на графике нет направленности в расположении точек εi , то
εi – случайные величины и применение МНК оправдано (теоретические y хорошо аппроксимируют фактические y).
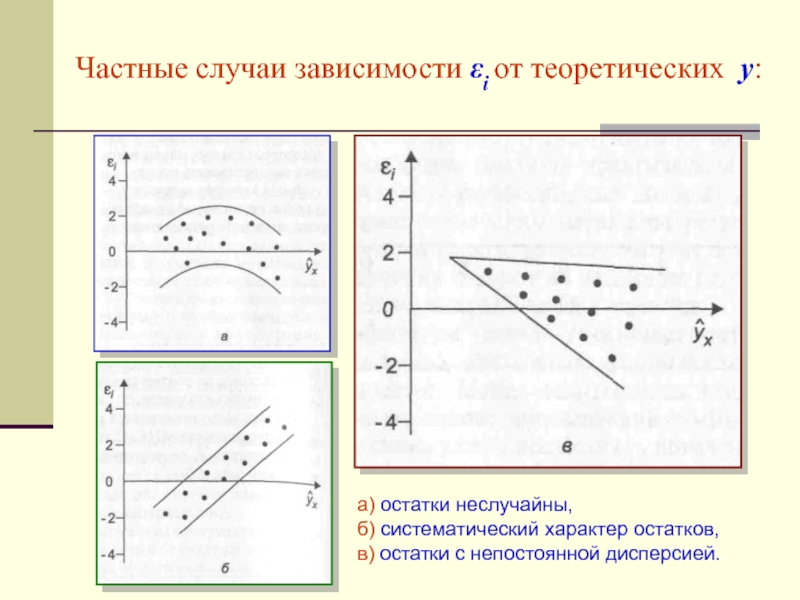
Слайд 33Частные случаи зависимости εi от теоретических y:
а) остатки неслучайны,
б)
систематический характер остатков, в) остатки с непостоянной дисперсией.
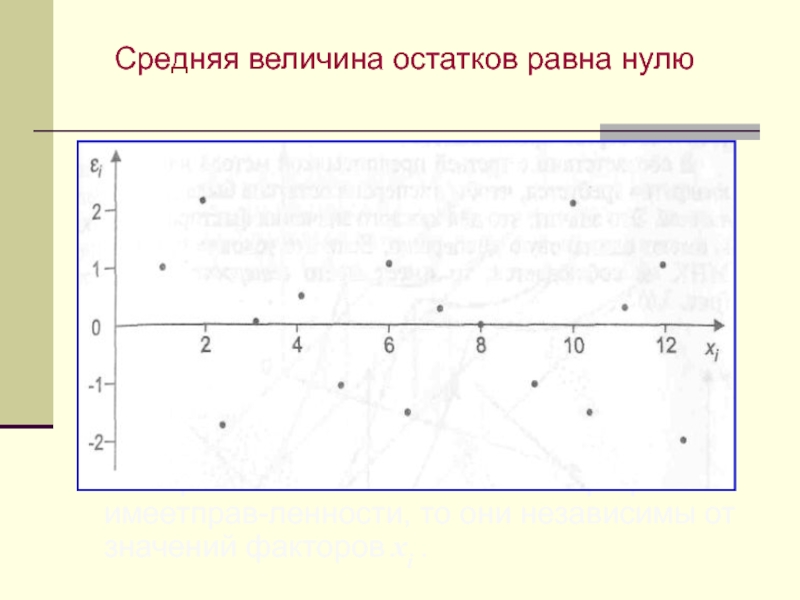
Слайд 34Средняя величина остатков равна нулю
Если расположение остатков на
графике не имеетправ-ленности, то они независимы от значений факторов xi
.
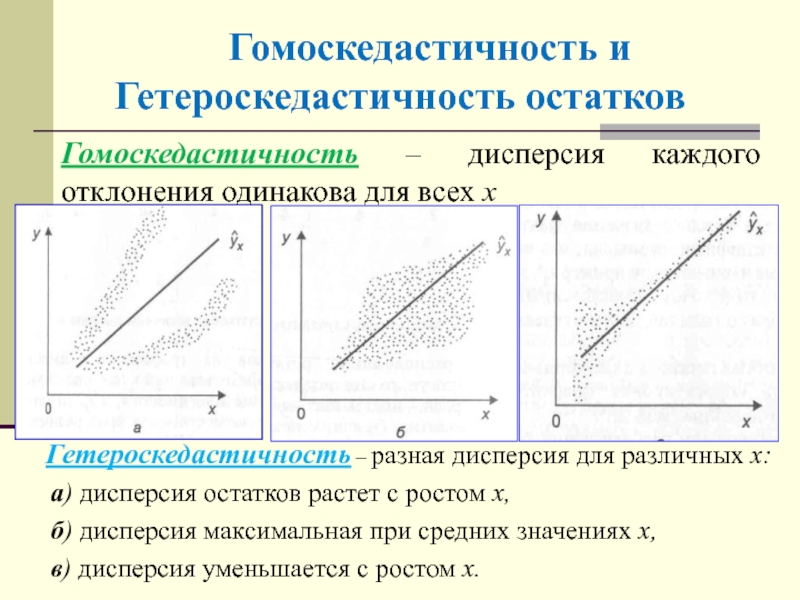
Слайд 35 Гомоскедастичность и Гетероскедастичность остатков
Гетероскедастичность – разная дисперсия
для различных x:
а) дисперсия остатков растет с ростом x,
б)
дисперсия максимальная при средних значениях x,
в) дисперсия уменьшается с ростом x.
Гомоскедастичность – дисперсия каждого отклонения одинакова для всех x
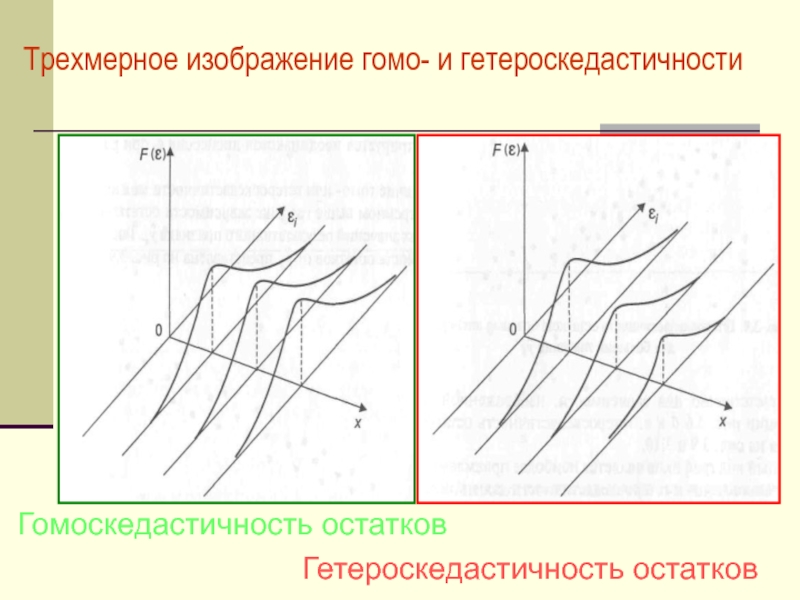
Слайд 36Трехмерное изображение гомо- и гетероскедастичности
Гомоскедастичность остатков
Гетероскедастичность остатков
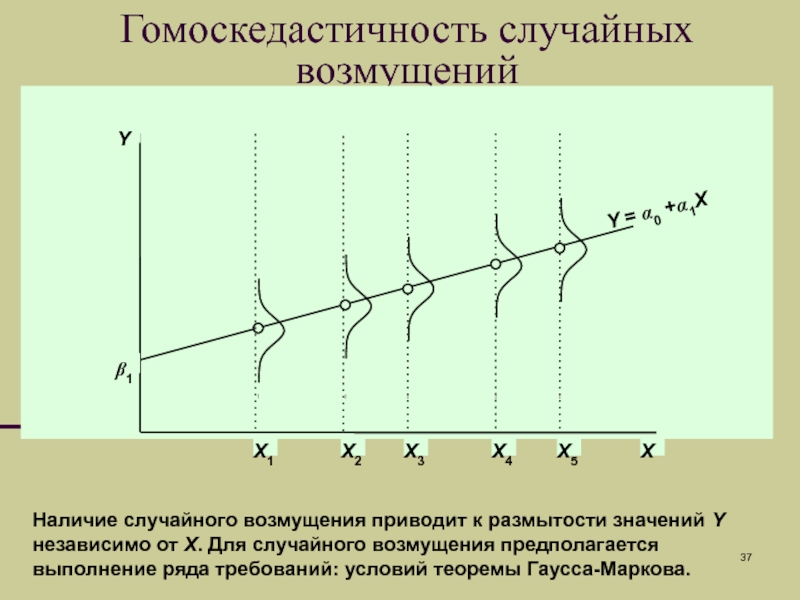
Слайд 37Гомоскедастичность случайных возмущений
b1
X
Y = a0 +a1X
Y
Наличие случайного возмущения приводит к
размытости значений Y независимо от X. Для случайного возмущения предполагается
выполнение ряда требований: условий теоремы Гаусса-Маркова.
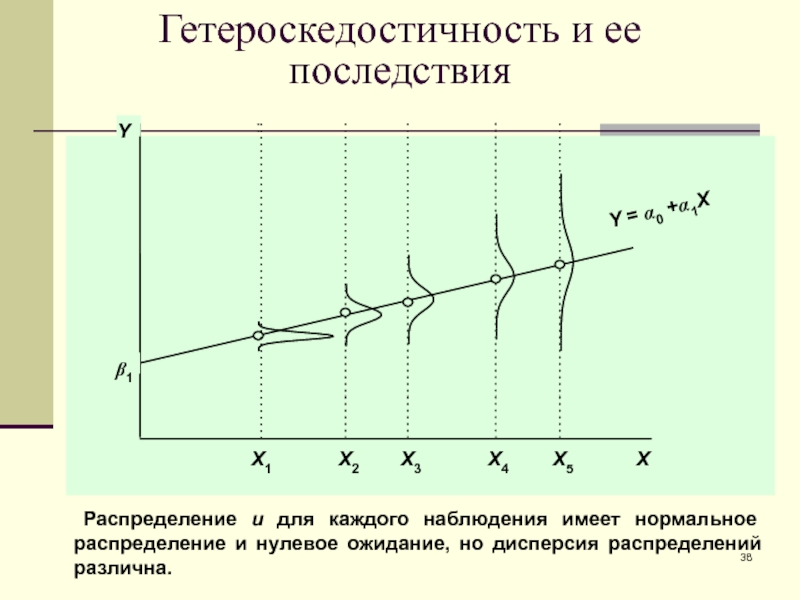
Слайд 38Гетероскедостичность и ее последствия
b1
X
Y = a0 +a1X
Y
Распределение u для
каждого наблюдения имеет нормальное распределение и нулевое ожидание, но дисперсия
распределений различна.
Слайд 39Гетероскедостичность и ее последствия
Условия обеспечивающие гомоскедастичность
(однородность) случайных возмущений:
1. Нормальное
распределение случайных возмущений для всех наблюдений.
2. Средние значения случайных возмущений
в каждом наблюдении равно нулю.
3. Распределения одинаковы для всех наблюдений.
Последствия нарушения условия гомоскедастичности случайных возмущений:
1. Потеря эффективности оценок коэффициентов регрессии, т.е. можно найти другие, отличные от МНК и более эффективные оценки.
2. Смещенность стандартных ошибок коэффициентов в связи с некорректностью процедур их оценки.
Слайд 40 Обнаружение гетероскедастичности
Гетероскедастичность можно выявить тремя тестами:
-
тест Голдфельда-Квандта (применяется при малом объеме выборки, нормальном распределении ε
и дисперсии остатков пропорциональной квадрату фактора);
- тест ранговой корреляции Спирмена;
- тест Глейзера.
Слайд 41Тест Голдфелда-Квандта
Данный тест предназначен для того, чтобы проверить гипотезу
об отсутствии гетероскедастичности случайных возмущений в схеме Гаусса-Маркова.
Случай уравнения парной регрессии.
Имеем спецификацию модели в виде:
Yt=a0 + a1xt+ut
Имеем выборку в объеме n наблюдений с переменными Yt и xt для оценки параметров модели.
Задача: проверить гипотезу об отсутствии гетероскедастичности в полученной модели.
Слайд 42Тест Голдфелда-Квандта
В основе теста лежат два предположения.
Случайные возмущения подчиняются нормальному
закону распределения.
Стандартные ошибки случайных возмущений σ(ut) пропорциональны значениям регрессора xt.
Слайд 43Алгоритм применения теста Голдфелда-Квандта
Шаг 1. Имеющаяся выборка из n наблюдений
сортируется (ранжируется) по возрастанию значений регрессора х.
Шаг 2. Полученная в
результате сортировки выборка делится на три примерно равные части (при малых объемах на 2 равные части).
Шаг 3. Для первой и третьей частей выборки строятся модели парной регрессии, т.е. для них вычисляются оценки параметров a0 и a1.
В результате получаются две модели парной регрессии (для каждой части общей выборки):
Y1=ã01 + ã11x +u1 (5.1)
Y3=ã03 + ã13x +u3 (5.2)
Исходя из принятых допущений, считается, что, если ошибки случайных возмущений в «первой» и «третьей» частях выборки будут равны, то условие гомоскедостичности выполняется.
Слайд 44Алгоритм применения теста Голдфелда-Квандта
Шаг 4. Для уравнений (5.1) и (5.2)
вычисляются значения RSS1 (ESS1) и RSS 3 (ESS3) - остаточные
суммы квадратов каждой из регрессий:
Где ESS(RSS) =Σ(ui2)=Σ(yi-ã0-ã1xi)2
Шаг 5. Проверяется гипотеза о равенстве σu1 и σu3.
Формируется случайная переменная GQ в виде:
В схеме Гаусса-Маркова переменная GQ имеет закон распределения Фишера.
Слайд 45Алгоритм применения теста Голдфелда-Квандта
Вычисленное значение GQ сравнивается с
критическим значением
Fкр(Pдов,n1,n3):
Если
GQ ≤ Fкр(Pдов,n1,n3)
и 1/GQ ≤ Fкр(Pдов,n1,n3),
то гипотеза о гомоскедастичности случайных возмущений принимается.
Случай уравнения множественной регрессии.
Yt=a0+a1x1t+a2x2t+a3x3t+ut
Сортировка проводится по величине z=|x1|+|x2|+|x3|.
Если тест дает отрицательный результат, алгоритм повторяется для каждого регрессора.
В результате обнаруживается регрессор вызывающий гетероскедастичность.
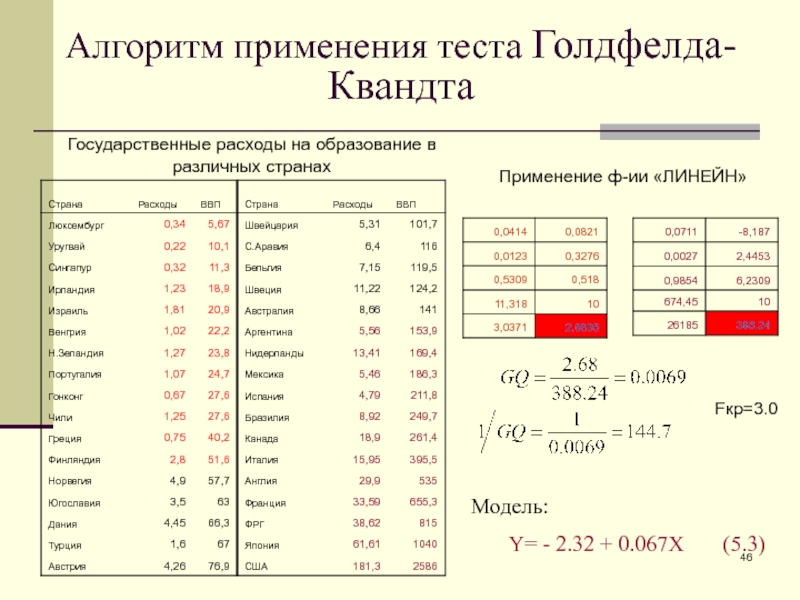
Слайд 46Алгоритм применения теста Голдфелда-Квандта
Государственные расходы на образование в различных странах
Fкр=3.0
Применение
ф-ии «ЛИНЕЙН»
Модель:
Y= - 2.32 + 0.067X
(5.3)
Слайд 47Метод исправления гетероскедастичности
Имеем:
1. Спецификацию модели: Yt=a0+a1x1t+a2x2t+a3x3t+ut (5.4)
2. Выборку наблюдений за переменными
{Y,x1,x2,x3}
3. Модель по этим данным гетероскедастична.
4. Известны значения σ(ut) в
каждом наблюдении.
Задача: преобразовать модель так, чтобы случайные возмущения были гомоскедастичны.
Слайд 48Метод исправления гетероскедастичности
Способ 1. Делится каждое уравнение наблюдений на свое
σ(ut) и получается:
Тогда дисперсия случайного возмущения в каждом уравнении наблюдений
есть:
Модель (5.2) в каждом уравнении наблюдения имеет одинаковые дисперсии случайного возмущения равные 1.
Недостаток способа – оценить σ(ut) не возможно!
(5.5)
Слайд 49Метод исправления гетероскедастичности
Способ 2.
Предполагаем, что σ(ut)=λxkt, где xkt регрессор «вызывающий»
гетероскедастичность. Пусть для примера это регрессор x2t.
Уравнение (5.4) делится на
значение этого регрессора.
Дисперсия случайного возмущения при этом есть:
(56)
Уравнения модели (5.3) имеют постоянную дисперсию случайного возмущения равную λ2.
Слайд 50Метод исправления гетероскедастичности
Рассмотренные способы устранения гетероскедастичности носят название «Взвешенный метод
наименьших квадратов».
Теорема. Если в схеме Гаусса-Маркова не выполняется предпосылка о
гомоскедастичности случайных возмущений, то наилучшей линейной процедурой оценки параметров модели является:
где: Р матрица ковариаций случайных возмущений в уравнения наблюдений:
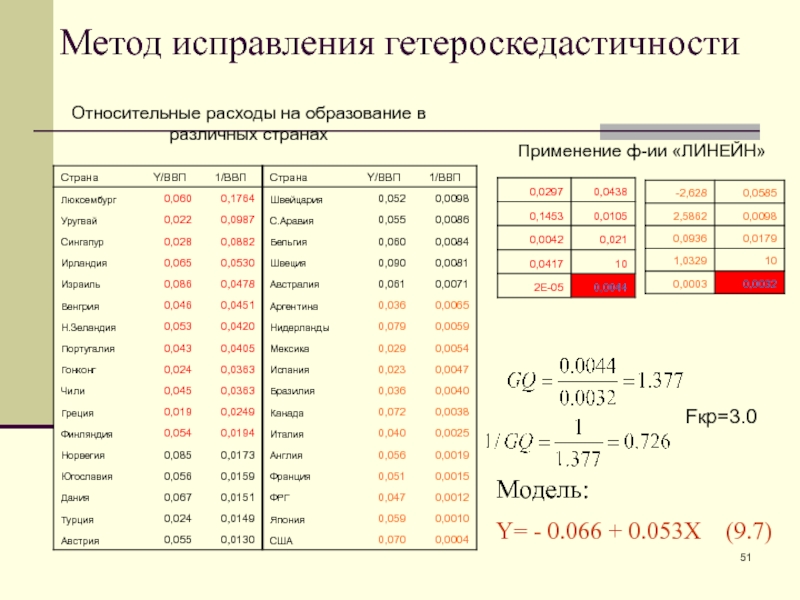
Слайд 51Метод исправления гетероскедастичности
Применение ф-ии «ЛИНЕЙН»
Относительные расходы на образование в различных
странах
Fкр=3.0
Модель:
Y= - 0.066 + 0.053X (9.7)
Слайд 52Модель:
Y = - 0.066 + 0.053X Гомоскедастичность
Модель (исходная):
Y = - 2.32 + 0.067X
Гетероскедастичность
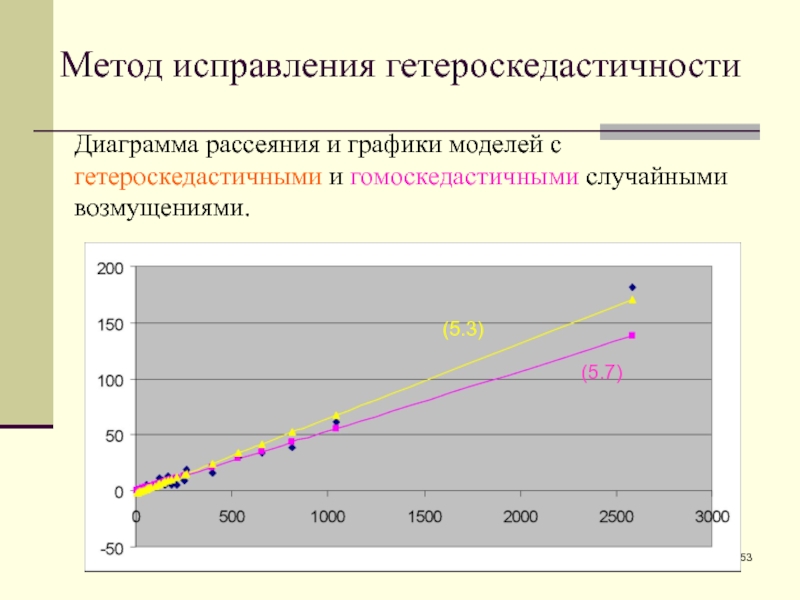
Слайд 53Метод исправления гетероскедастичности
(5.7)
(5.3)
Диаграмма рассеяния и графики моделей с гетероскедастичными и
гомоскедастичными случайными возмущениями.