Слайд 1МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Задачи оптимизации
Слайд 2Метод крутого восхождения
Оптимизация процесса представляет собой целенаправленный поиск значений влияющих
факторов, при которых достигается экстремум критерия оптимальности.
Важно отметить, что как
влияющие факторы, так и функции отклика могут изменяться только в определенных пределах. Так, концентрации реагентов не могут быть отрицательными, температура и давление в аппарате не могут превышать безопасных пределов, себестоимость продукции должна быть не выше плановой и т. п. Следовательно, оптимизацию процессов, как правило, осуществляют в условиях ограничений на влияющие факторы и функции отклика.
Известные ученые Д. Бокс и К. Уилсон предложили использовать для оптимизации результаты полного или дробного факторного эксперимента [1]. Сущность такой оптимизации состоит в следующем.
Слайд 4Метод крутого восхождения
Ставят ряд опытов в точках, лежащих на градиенте.
Для этого выбирается базовый фактор, который оказывает наибольшее воздействие на
параметр, т.е. для которого произведение biΔxi является наибольшим; здесь Δxi – интервал варьирования i-го фактора.
Затем для базового фактора выбирают шаг движения , с которым будет осуществляться оптимизация. Обычно . Пусть для примера фактор x1 будет определяющим, тогда вычисляют отношение
Слайд 6Метод крутого восхождения
По данным опытов устанавливают положение частного экстремума в
данном направлении
Движение к оптимуму прекращают также когда значения одного или
нескольких факторов или функций отклика вышли на границы допустимых значений.
Слайд 7Метод крутого восхождения
В точке частного экстремума ставят новый факторный эксперимент.
Находят уравнение регрессии. Проверяют его адекватность. Ищут направление нового градиента
и осуществляют «крутое восхождение» по нему в соответствии с изложенным ранее.
Поиск прекращается, когда линейная модель оказывается неадекватной. Это означает, что достигнута область оптимума. В ней ставят эксперимент второго порядка, по которому уточняют положение оптимума, или просто принимают наилучший из полученных результатов.
Если же в области оптимума не удается получить адекватного уравнения регрессии, то проводят анализ выбранных переменных и добавляют новые влияющие факторы либо увеличивают точность эксперимента.
Слайд 8Пример
Пусть в результате полного факторного эксперимента получено адекватное уравнение регрессии
y1 = 35,6+1,95X1–1,35X2.
Здесь y1 – выход продукта реакции, x1 –
температура, x2 – концентрация реагента. Введем также в рассмотрение функцию отклика у2, характеризующую скорость химической реакции (кмоль·м–3·ч–1).
Требуется выполнение условия y2 ≥ 2,5.
Решение. Допустим, что ограничения на влияющие факторы имеют вид
30о ≤ x1 ≤ 120о,
10 % ≤ x2 ≤ 70 %.
Оптимизируем выход продукта реакции методом крутого восхождения.
В качестве базового фактора возьмем температуру и примем шаг движения на крутом восхождении 4°, тогда
Слайд 9Пример
Здесь x1 взят по условиям предыдущего примера.
Шаг по концентрации на
крутом восхождении можно рассчитать по уравнению
Для удобства ведения эксперимента
шаги движения, рассчитанные по данной формуле , можно несколько округлять.
В данном случае удобно принять -0,5 %.
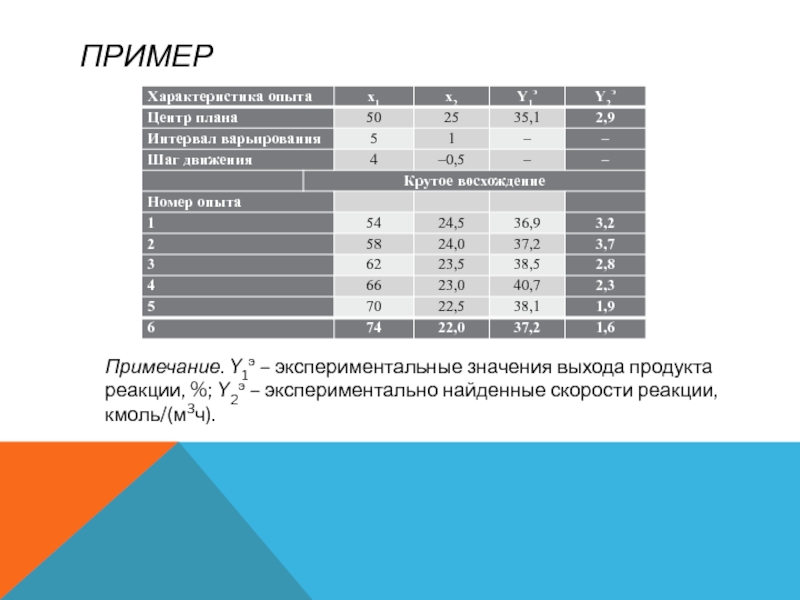
Результаты опытов, выполненных по методу крутого восхождения, приведены в таблице
Слайд 10Пример
Примечание. Y1э – экспериментальные значения выхода продукта реакции, %; Y2э
– экспериментально найденные скорости реакции, кмоль/(м3ч).
Слайд 11Пример
Как видно из табл. в опыте №4 достигнут максимальный выход
продукта реакции, однако скорость процесса в этом случае меньше допустимого
значения.
По-видимому, оптимальным режимом процесса следует считать условия опыта №3.
Ограничения на х1 и х2 в ходе оптимизации не нарушены.
Слайд 12Используемая литература
1. Саутин С.Н. Планирование эксперимента в химии и химической
технологии / С.Н. Саутин. Л. : Химия, 1975.