Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы оптимального планирования экспериментов
Содержание
- 1. Методы оптимального планирования экспериментов
- 2. Историческая справкаИсторически планирование эксперимента появилось значительно раньше,
- 3. Планирование экспериментовЭто комплекс мероприятий, направленных на эффективную
- 4. Основные понятияОбычно модели рассматриваются как черные ящики,
- 5. Требования к выбору функции откликаОна должна быть:Количественной
- 6. Требования к выбору параметровфакторы должен быть регулируемыми
- 7. Ряд требований предъявляются одновременно как к факторам
- 8. Построение планов экспериментовПлана строится от центральной точки
- 9. Решаемые задачиВ зависимости от поставленных задач решения
- 10. выполнить крутое восхождения в область экстремуму с
- 11. План-матрицы полного и дробного факторных экспериментовФакторные эксперименты
- 12. Свойства матриц ПФЭПлан эксперимента обладает ортогональностью:симметричностью:нормировкой:рототабельностью – равенством и минимальностью дисперсий по всему факторному пространству
- 13. Насыщенность плановОднопараметрическая модель является полностью насыщенной, находим
- 14. Дробный факторный экспериментДля трехпараметрическая модель имеются четыре
- 15. Заполнение плана даннымиГотовим таблицу с исходными даннымиФормируем
- 16. Сбор и анализ априорной информации в научно-технической
- 17. Анализ априорной информации Общие понятияВ основе метода
- 18. Анализ априорной информации Опросные карточкиРассмотрим пример, мы
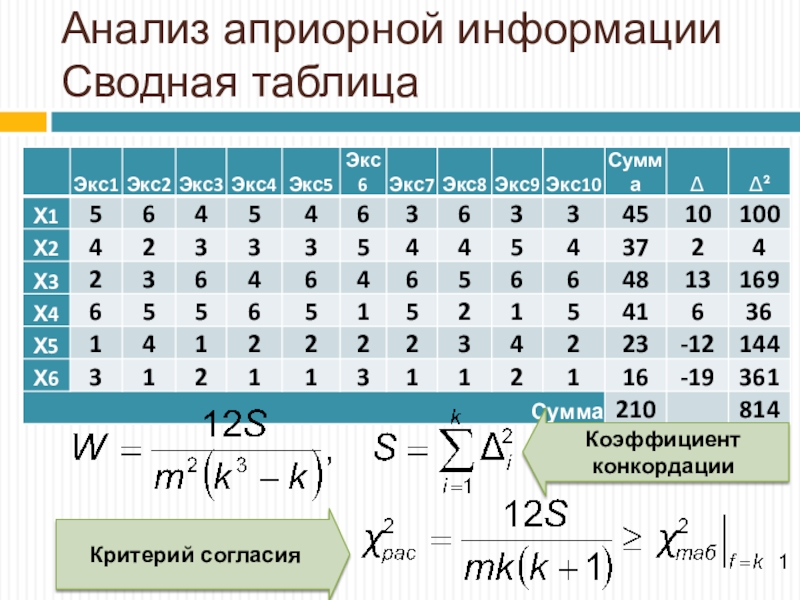
- 19. Анализ априорной информации Сводная таблицаКритерий согласияКоэффициент конкордации
- 20. Анализ априорной информации Гистограмма параметровПо гистограмме хорошо
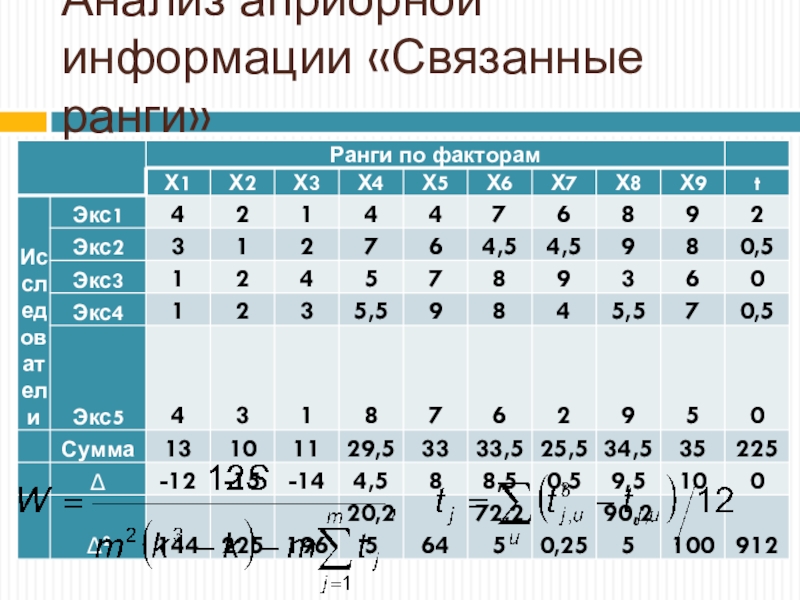
- 21. Анализ априорной информации «Связанные ранги»
- 22. Метод случайного баланса (МСБ) Общие понятияМСБ предполагает
- 23. Метод случайного баланса Общие понятияИдея метода заключается
- 24. Метод случайного баланса Построение матрицы1 шаг2 шаг3 шаг
- 25. Метод случайного баланса Расчет размаховОбычным приравниванием (=Ячейка)
- 26. Метод случайного баланса Корректировка функцииРедактируем формулу:=G25+ЕСЛИ(C25=-1;$C$35;0)Для построения
- 27. Метод случайного баланса Определение оставшихся размаховЕсли формулы
- 28. Метод случайного баланса Построение диаграммы рассеянияЕсли при
- 29. Выделяем нужный столбец параметра и, удерживая клавишу
- 30. Метод случайного баланса Заключение по результатамСтроим вспомогательную
- 31. Алгоритм планирования экспериментаВыбираем центральную точку факторного и
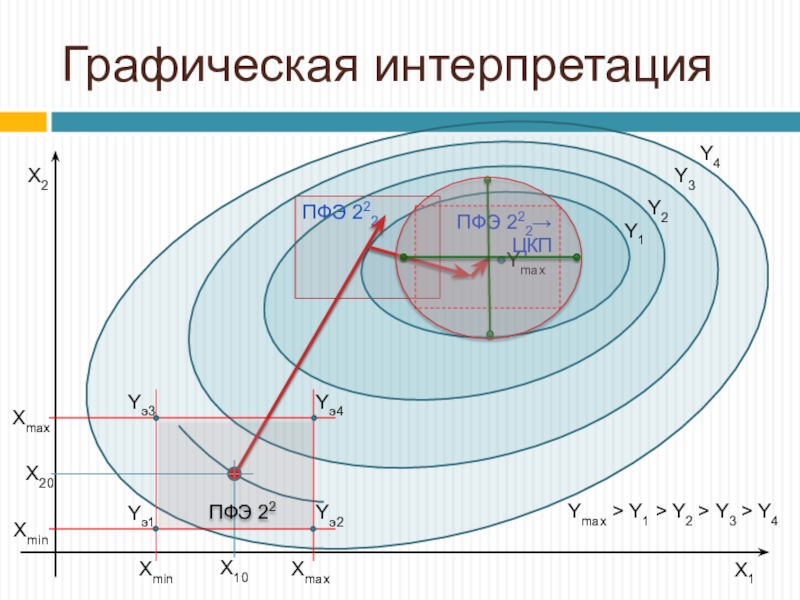
- 32. ПФЭ 222Графическая интерпретацияX1X2YmaxY1Y2Y3Y4Ymax > Y1 > Y2 > Y3 > Y4Yэ1ПФЭ 222→ ЦКП
- 33. Полный факторный эксперимент основы методаОсновой метода является
- 34. Полный факторный эксперимент основные предпосылкиВ основе данных
- 35. Полный факторный эксперимент однородность дисперсийТак как мы
- 36. При соблюдении данного условия однородность дисперсий принимается
- 37. Полный факторный эксперимент значимость коэффициентовЕсли дисперсии однородны,
- 38. Полный факторный эксперимент адекватность моделиАдекватность модели проверяется
- 39. Слайд 39
- 40. Слайд 40
- 41. Другие реализации ПФЭДопустимы и другие реализации ПФЭ:С
- 42. Дробный факторный экспериментПолный факторный эксперимент является удобным
- 43. Взяв за основу трехфакторное пространство можно получить
- 44. Крутое восхождение в область экстремумаПолучив адекватную модель
- 45. Слайд 45
- 46. Слайд 46
- 47. Центральные композиционные планы, общие положенияЗадачами планов второго
- 48. Центральные композиционные планы, общие положенияТакие планы состоят
- 49. Точки полного факторного эксперимента«Звездные» точки их радиус α определяется от типа планаЦентральная точка
- 50. Величина плеча «звездной» точки для ортогональных планов
- 51. Сравнение планов
- 52. Методики расчетов ЦКПРасчеты по результатам ЦКОП похожи
- 53. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Методы оптимального планирования экспериментов
Воробьев Евгений Сергеевич
Моделирование химическо-технологических процессов
Тема №5
Дисциплина
Слайд 2Историческая справка
Исторически планирование эксперимента появилось значительно раньше, чем были сформулированы
Слайд 3Планирование экспериментов
Это комплекс мероприятий, направленных на эффективную постановку опытов. Основная
цель планирования эксперимента – достижение максимальной точности измерений при минимальном
количестве проведенных опытов и сохранении статистической достоверности результатов.Планирование эксперимента применяется при поиске оптимальных условий, построении интерполяционных формул, выборе значимых факторов, оценке и уточнении констант теоретических моделей и др.
Все эти методы объединяются под названием планирования оптимального эксперимента. В их основе заложены принципы поэтапного решения задачи, в котором на каждом из этапов повышается сложность модели с использованием большинства результатов предыдущих опытов, что обеспечивает минимум экспериментов для получения окончательного решения.
Слайд 4Основные понятия
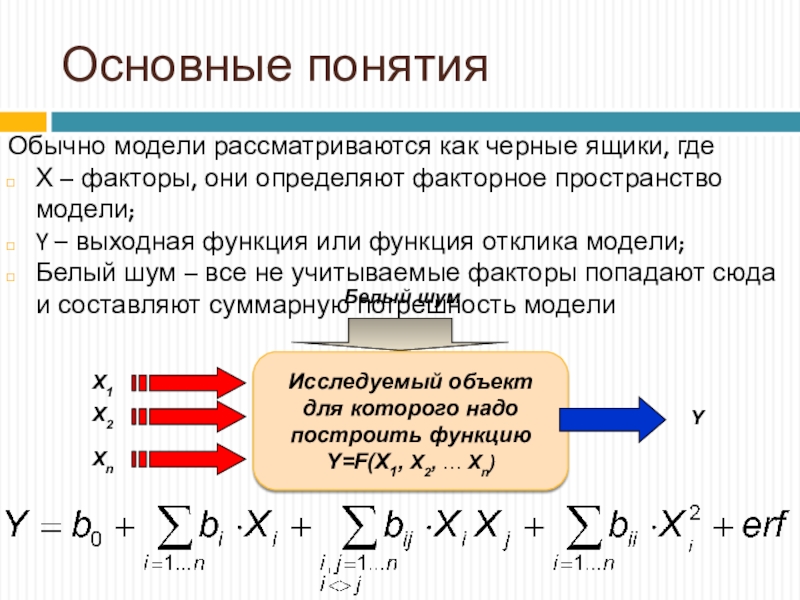
Обычно модели рассматриваются как черные ящики, где
Х – факторы,
они определяют факторное пространство модели;
Y – выходная функция или функция
отклика модели;Белый шум – все не учитываемые факторы попадают сюда и составляют суммарную погрешность модели
Слайд 5Требования к выбору функции отклика
Она должна быть:
Количественной должна измеряться; однозначно
оценивать (измерять) работу объекта исследования;
Статистически эффективной, иметь возможно меньшую
дисперсию при проведении опытов;Отражать как можно более широкий спектр функций исследуемого явления, обладать универсальностью (практически это требование обеспечить трудно, тогда рекомендуют пользоваться обобщенной переменной);
иметь достаточно четкий физический смысл.
Удачный выбор выходной переменной определяется уровнем знания технологии и объекта.
Слайд 6Требования к выбору параметров
факторы должен быть регулируемыми в интервале значений
от хmin до хmax;
точность измерения и управления фактором должна быть
известна и достаточно высока (хотя бы на порядок выше точности измерения выходной функции), низкая точность измерения фактора уменьшает воспроизведения эксперимента;связь между факторами должна быть как можно меньшей (в пределе должна отсутствовать), это называют однозначностью факторов, что соответствует независимости их друг от друга.
Слайд 7Ряд требований предъявляются одновременно как к факторам так и к
выходной функции, они должны иметь общие области определения.
При нахождении
факторов в их заданных пределах, значение выходной функции должно оставаться в своих границах. Между факторами и выходной функцией должно быть однозначное соответствие (причинно-следственная связь), которую мы обычно и хотим найти.
Слайд 8Построение планов экспериментов
Плана строится от центральной точки с заданными шагами,
для автомасштабирования факторов факторное пространство преобразуется с безразмерную систему координат
(Z1, Z2):Функция отклика
Кодированное значение
Натуральное значение
Слайд 9Решаемые задачи
В зависимости от поставленных задач решения могут быть остановлены
на любом этапе согласно начальной постановке:
определить значения выходной функции и
значимость входных параметров (их вклад в исследуемую функцию) в заданном факторном пространстве;построить линейную модель для САР или поиска направления движения в область экстремума функции по наикратчайшему пути вдоль её градиента от центральной точки построенного плана;
Слайд 10выполнить крутое восхождения в область экстремуму с целью нахождения более
лучшей точки для ведения процесса или работы аппарата;
попав в область
экстремума построение плана второго порядка для описания процесса или аппарата более сложных зависимостей, описывающих объекты в области экстремумов.Слайд 11План-матрицы полного и дробного факторных экспериментов
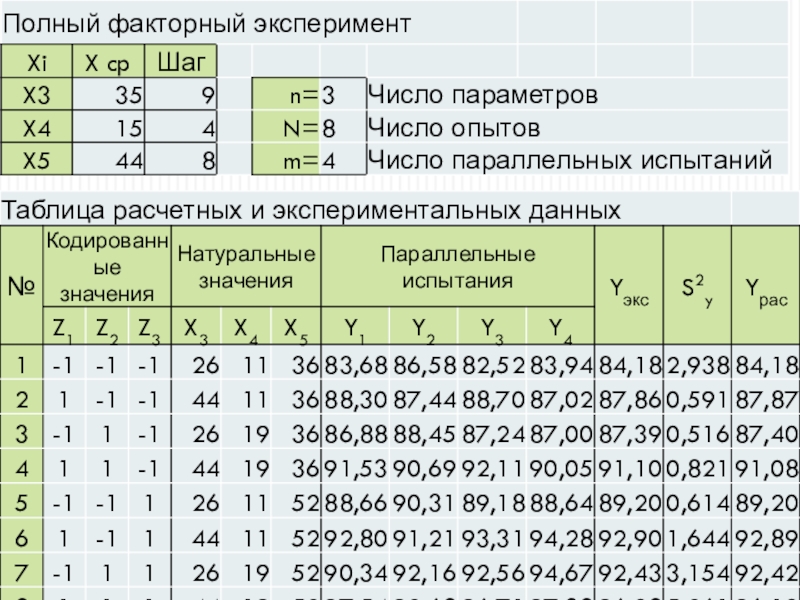
Факторные эксперименты первого порядка построены
на линейных моделях с использованием классических МНК и дисперсионного статистического
анализа. Они реализуются возможные комбинации факторов на всех выбранных уровнях. Общее число опытов для полного факторного эксперимента в случае, когда реализуются все комбинации факторов, равно N=2nn=3, N=8
Слайд 12Свойства матриц ПФЭ
План эксперимента обладает ортогональностью:
симметричностью:
нормировкой:
рототабельностью – равенством и минимальностью
дисперсий по всему факторному пространству
Слайд 13Насыщенность планов
Однопараметрическая модель является полностью насыщенной, находим два коэффициента на
основании двух опытов, для двухпараметрической модели остается один опыт. Трёх
и более параметрические модели становятся ненасыщенными и имеются опыты, которые можно использовать для других факторов, что реализуется в дробных планах.Слайд 14Дробный факторный эксперимент
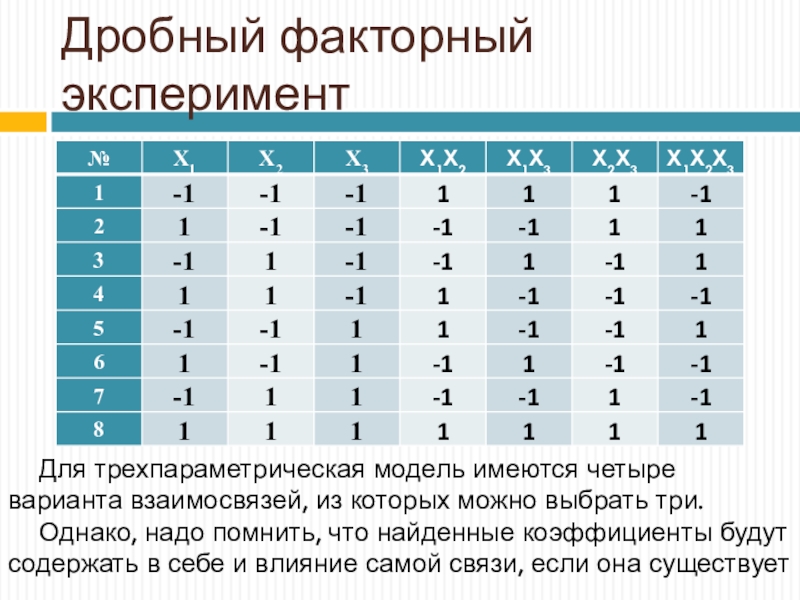
Для трехпараметрическая модель имеются четыре варианта взаимосвязей, из
которых можно выбрать три.
Однако, надо помнить, что найденные коэффициенты будут
содержать в себе и влияние самой связи, если она существуетСлайд 15Заполнение плана данными
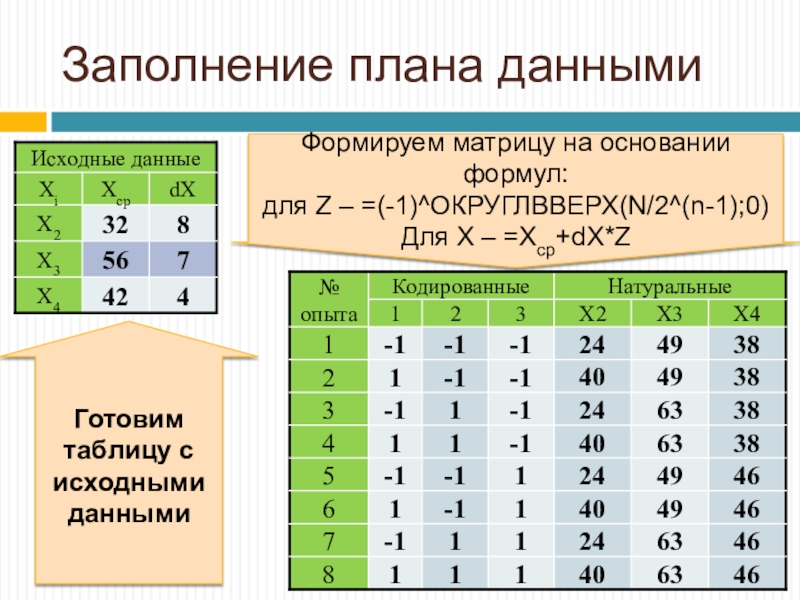
Готовим таблицу с исходными данными
Формируем матрицу на основании
формул:
для Z – =(-1)^ОКРУГЛВВЕРХ(N/2^(n-1);0)
Для Х – =Xcp+dX*Z
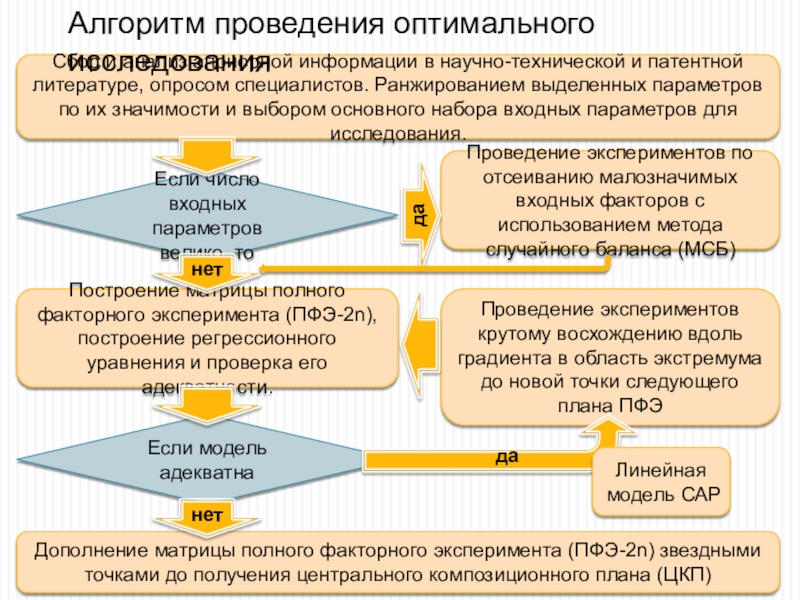
Слайд 16Сбор и анализ априорной информации в научно-технической и патентной литературе,
опросом специалистов. Ранжированием выделенных параметров по их значимости и выбором
основного набора входных параметров для исследования.Если число
входных параметров велико, то
Проведение экспериментов по отсеиванию малозначимых входных факторов с использованием метода случайного баланса (МСБ)
Построение матрицы полного факторного эксперимента (ПФЭ-2n), построение регрессионного уравнения и проверка его адекватности.
Дополнение матрицы полного факторного эксперимента (ПФЭ-2n) звездными точками до получения центрального композиционного плана (ЦКП)
Если модель
адекватна
Проведение экспериментов крутому восхождению вдоль градиента в область экстремума до новой точки следующего плана ПФЭ
нет
нет
да
да
Алгоритм проведения оптимального исследования
Линейная модель САР
Слайд 17Анализ априорной информации Общие понятия
В основе метода лежит однопараметрический качественный
дисперсионный анализ (анализируемые уровни выражены качественными значениями (именами факторов) и
их значения заменены рангами). Наиболее значимым параметром является тот, который имеет наименьшую сумму рангов.Согласованность экспертов оценивается через коэффициент конкордации и его значимость проверяется с помощью критерия Пирсона.
В качестве уровней дисперсионного анализа выступают оцениваемые факторы, а параллельные испытания по каждому из них формируются из мнения экспертов.
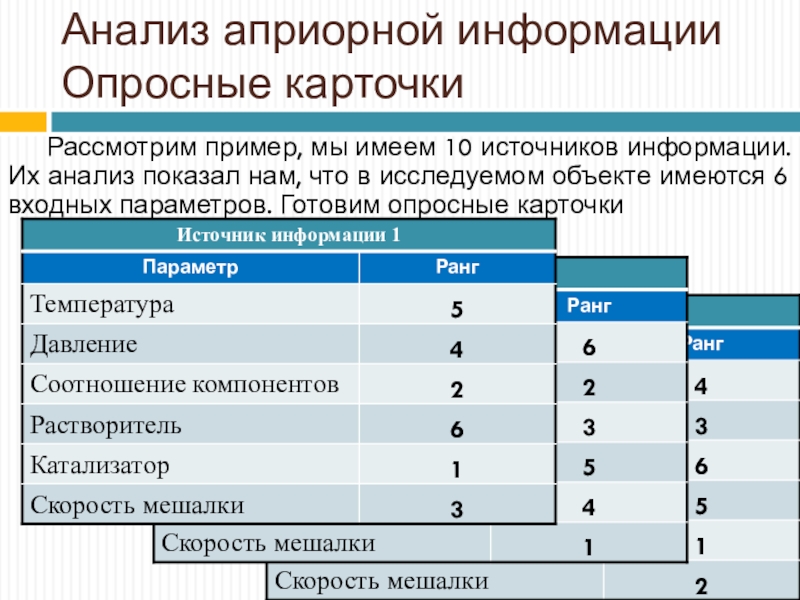
Слайд 18Анализ априорной информации Опросные карточки
Рассмотрим пример, мы имеем 10 источников
информации. Их анализ показал нам, что в исследуемом объекте имеются
6 входных параметров. Готовим опросные карточкиСлайд 20Анализ априорной информации Гистограмма параметров
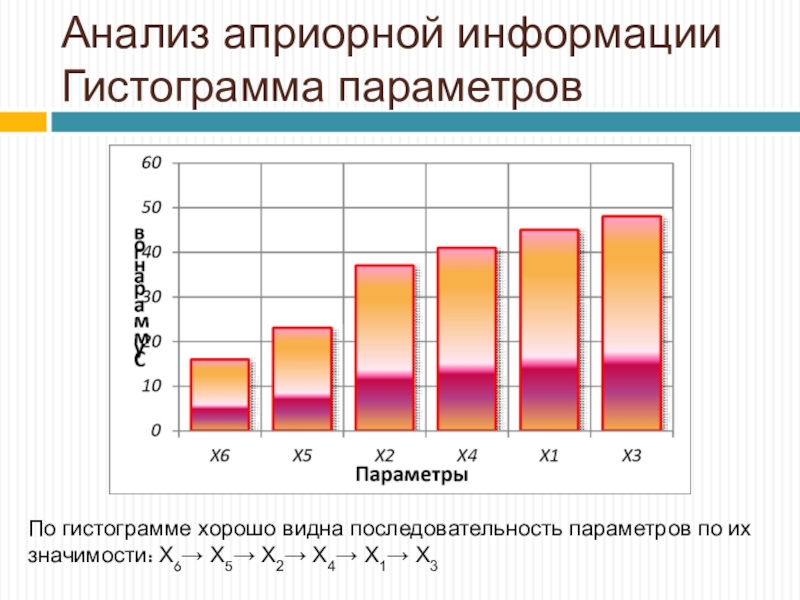
По гистограмме хорошо видна последовательность параметров
по их значимости: Х6→ Х5→ Х2→ Х4→ Х1→ Х3
Слайд 22Метод случайного баланса (МСБ)
Общие понятия
МСБ предполагает определение оценки влияния каждого
фактора на выходную функцию при условии наличия линейной связи в
интервале от минимального до максимального значения параметра.Оценки влияния каждого фактора рассматриваются как независимые от остальных, то есть их влияние рассматривается как «белый шум».
Наличие в исследуемом интервале экстремумов функции приводит к ошибочным результатам, так же к ошибкам ведут неудачно выбранные границы интервалов по разным параметрам.
Слайд 23Метод случайного баланса
Общие понятия
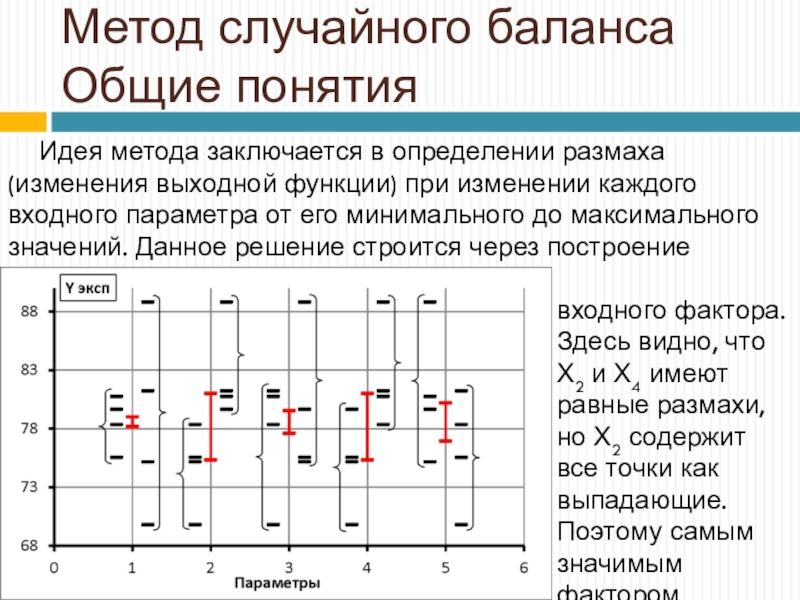
Идея метода заключается в определении размаха (изменения
выходной функции) при изменении каждого входного параметра от его минимального
до максимального значений. Данное решение строится через построение диаграмм рассеяния для каждоговходного фактора. Здесь видно, что Х2 и Х4 имеют равные размахи, но Х2 содержит все точки как выпадающие. Поэтому самым значимым фактором является Х2
Слайд 25Метод случайного баланса
Расчет размахов
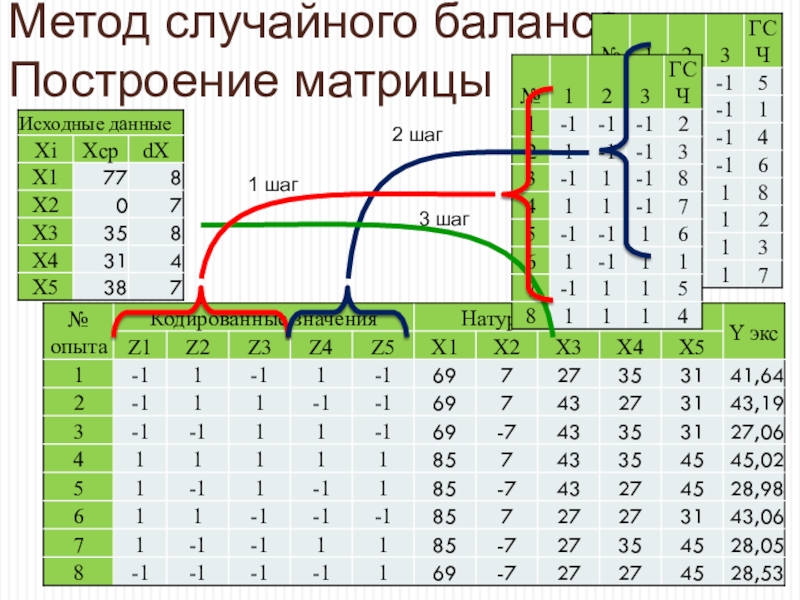
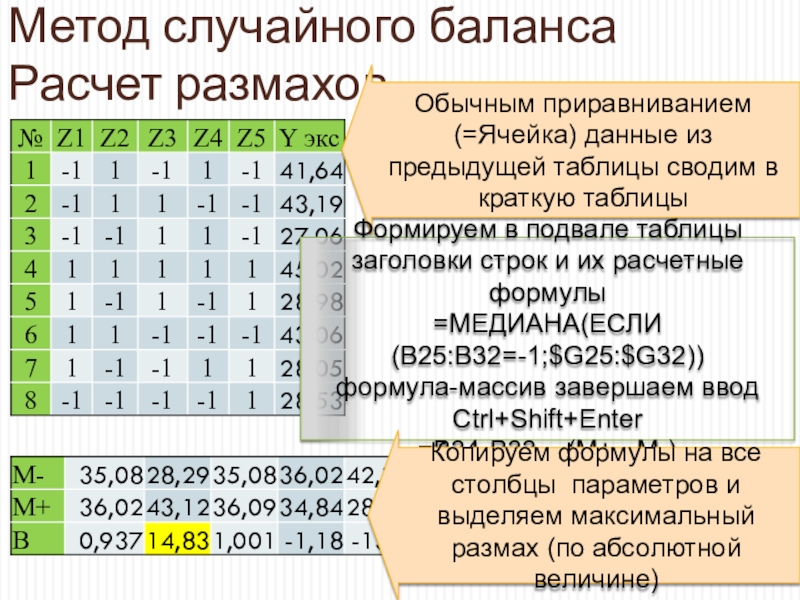
Обычным приравниванием (=Ячейка) данные из предыдущей таблицы
сводим в краткую таблицы
Формируем в подвале таблицы заголовки строк
и их расчетные формулы=МЕДИАНА(ЕСЛИ(B25:B32=-1;$G25:$G32))
формула-массив завершаем ввод Ctrl+Shift+Enter
=B34-B33 – (М+ - М-)
Копируем формулы на все столбцы параметров и выделяем максимальный размах (по абсолютной величине)
Слайд 26Метод случайного баланса
Корректировка функции
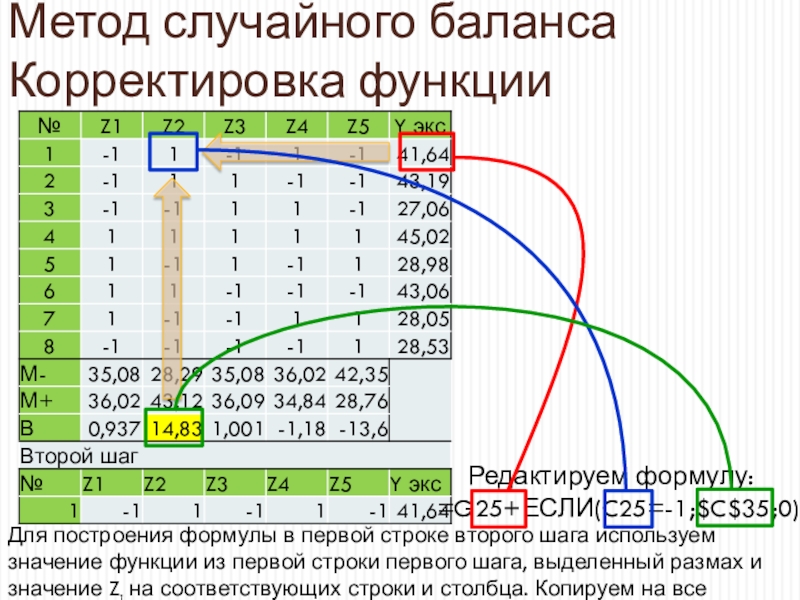
Редактируем формулу:
=G25+ЕСЛИ(C25=-1;$C$35;0)
Для построения формулы в первой строке
второго шага используем значение функции из первой строки первого шага,
выделенный размах и значение Zi на соответствующих строки и столбца. Копируем на все значения Y для второго шагаСлайд 27Метод случайного баланса
Определение оставшихся размахов
Если формулы введена правильно и потом
скопирована на остальные ячейки столбца Y, то размах для выбранного
Zi должен стать равным 0. Удаляем над этим нулем формулы для вычисления медиан. Находим следующее наибольшее значение размаха (по абсолютной величине), выделяем его цветом. Копируем всю таблицу данных с блоком формул и вставляем все ниже соблюдая число пропущенных строк между таблицами. Корректируем формулу для расчета Y, перемещая размах на новую, выделенную цветом, ячейку и значение Zi в столбец над размахом.Если все выполнено правильно, то очередной размах станет равным 0. Повторяем операцию до тех пор, пока для всех входных параметров не будут определены их размахи.
Слайд 28Метод случайного баланса
Построение диаграммы рассеяния
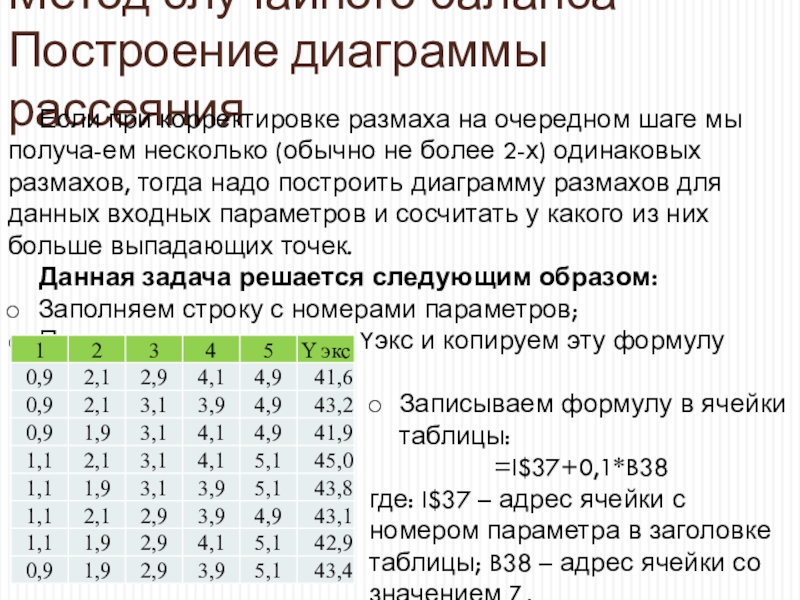
Если при корректировке размаха на очередном
шаге мы получа-ем несколько (обычно не более 2-х) одинаковых размахов,
тогда надо построить диаграмму размахов для данных входных параметров и сосчитать у какого из них больше выпадающих точек.Данная задача решается следующим образом:
Заполняем строку с номерами параметров;
Приравниваем заголовок Yэкс и копируем эту формулу вниз;
Записываем формулу в ячейки таблицы:
=I$37+0,1*B38
где: I$37 – адрес ячейки с номером параметра в заголовке таблицы; B38 – адрес ячейки со значением Zi.
Скопируем формулу на всю таблицу.
Слайд 29Выделяем нужный столбец параметра и, удерживая клавишу Ctrl выделяем столбец
Yэкс;
Строим диаграмму – точечная – только маркеры;
Вызываем команду «Выбрать данные»
и добавляем следующий параметр с набором Yэкс;Настраиваем диаграмму, чтобы хорошо было видно точки и считаем выпавшие из них.
На графике внизу показана диаграмма для всех пяти входных параметров, выпавшие точки по параметрам имеют следующие значения: X1 – 0; X2 – 8; X3 – 2; X4 – 6; X5 – 2.
Слайд 30Метод случайного баланса
Заключение по результатам
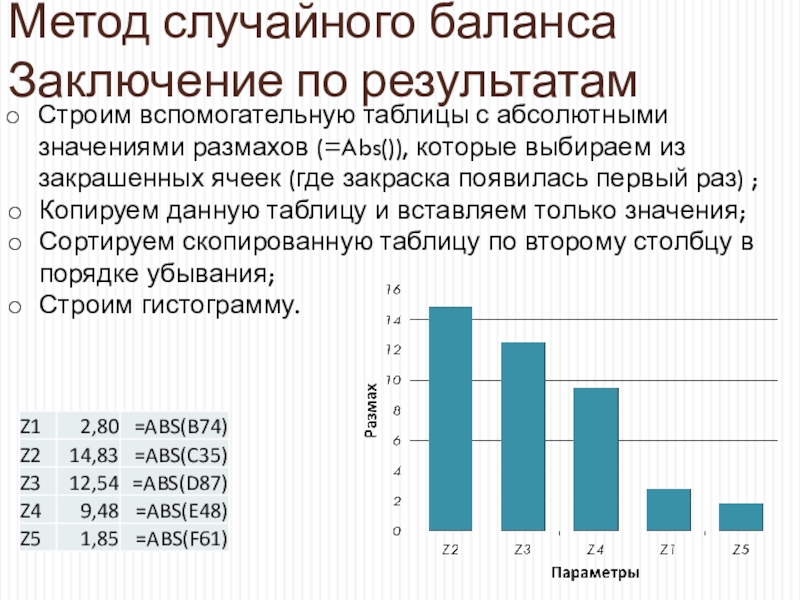
Строим вспомогательную таблицы с абсолютными значениями
размахов (=Abs()), которые выбираем из закрашенных ячеек (где закраска появилась
первый раз) ;Копируем данную таблицу и вставляем только значения;
Сортируем скопированную таблицу по второму столбцу в порядке убывания;
Строим гистограмму.
Слайд 31Алгоритм планирования эксперимента
Выбираем центральную точку факторного и вокруг неё строим
полный (дробный) факторный эксперимент. Выполняем испытания, проводим обработку данных, получаем
регрессионную модель, которая описывает наш объект.Если модель адекватна, то можно использовать данную модель для управления процессом в этой локальной области или воспользовавшись методом крутого восхождения найти новую точку в которой построить следующий план.
В противном случае (модель не адекватная) мы оказались в области экстремума и необходимо повышать сложность модели до второго порядка.
Графически алгоритм представлен далее.
Слайд 33Полный факторный эксперимент
основы метода
Основой метода является регрессионный анализ данных в
котором по результатам эксперимента на объекте исследования можно найти его
математическую модель. Полученная модель (обычно полином) называется уравнением регрессии.Степень приближения уравнения регрессии к реальному объекту зависит не только от экспериментальных данных, но и от метода построения полинома. В качестве такого метода обычно выбирают метод наименьших квадратов, являющийся частным случаем метода максимума правдоподобия для случайных переменных с нормальным законом распределением.
Уравнение подвергается статистическому анализу, основанному на оценках различных дисперсий: проверяются однородность дисперсий, значимость коэффициентов и адекватность уравнения регрессии.
Слайд 34Полный факторный эксперимент
основные предпосылки
В основе данных решений лежат несколько статистических
предпосылок, выполнение которых гарантирует достоверность анализа полученной математической модели:
Выходная переменная
— случайная величина с нормальным законом распределением; факторы — неслучайные величины; это означает, что ошибки в управлении факторами по крайней мере на порядок меньше ошибок при измерении выходной переменной.Связь между факторами отсутствует или её надо учитывать.
Дисперсии выходной переменной однородны в любой точке факторного пространства.
Исследуемый объект лишен динамических свойств (рассматриваются стационарные режимы объекта).
Слайд 35Полный факторный эксперимент
однородность дисперсий
Так как мы обычно проводим несколько серий
испытаний в каждой точке факторного пространства, и получаем статистические оценки
для каждой точки. Анализ этих данных может указать на наличие областей с большими погрешностями. Данная проверка выполняется с помощью критерия Кохрена, по следующей схема:где: Si2 – строчная дисперсия с серии из m – параллельных опытов в плане с N – точками в плане эксперимента.
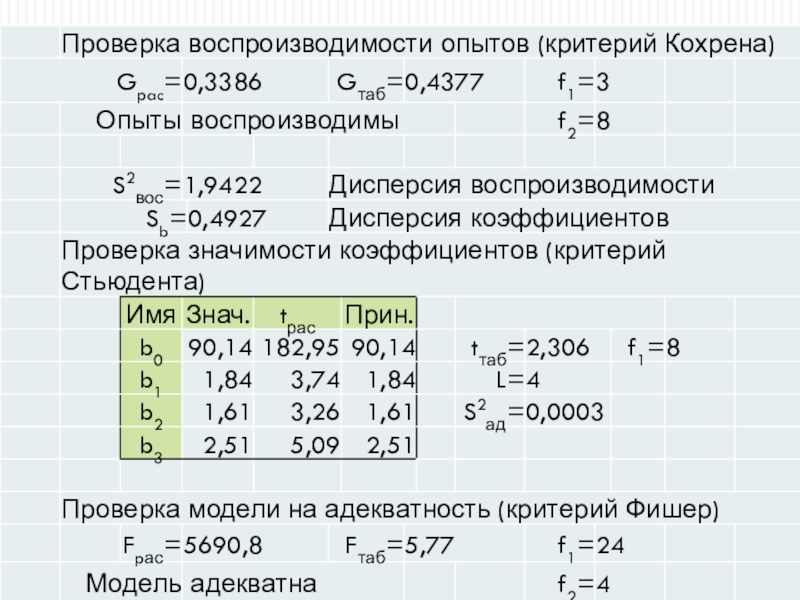
Слайд 36При соблюдении данного условия однородность дисперсий принимается и расчет продолжается
далее.
В противном случае ищется причина неоднородности дисперсий. Это обычно случайные
или систематические ошибки во время экспериментов.Наличие случайных ошибок обычно возникает при неоднородности строчных дисперсий в одном опыте. Систематические ошибки возникаю в нескольких строках матрицы плана и связаны с низкой точностью методики из-за малого шага изменения параметра или при влиянии не учитываемого фактора, который становится значимым в определенных условиях данного плана.
Слайд 37Полный факторный эксперимент
значимость коэффициентов
Если дисперсии однородны, определяем коэффициенты уравнения регрессии
и проверяем их значимость с помощью критерия Стьюдента:
где: zi,j –
кодированные значения параметров; yi – средние значения функции.Если коэффициент не значим, то его значение приравнивается нулю, это говорит о том, что либо выбран недостаточный интервал варьирования параметра или в интервале имеется экстремум функции
Слайд 38Полный факторный эксперимент
адекватность модели
Адекватность модели проверяется с помощью критерия Фишера:
Если
модель адекватна, то она может использоваться для САР или на
её основании можно реализовать крутое восхождение. При неадекватности модели и нулевых или маленьких значениях коэффициентов надо переходить к моделям второго порядка. Другая причина неадекватности – недостаточный интервал или низкая точность методики.Слайд 41Другие реализации ПФЭ
Допустимы и другие реализации ПФЭ:
С проведением параллельных испытаний
в одной точке плана, что несколько упрощает расчет и исключает
проверку на однородность дисперсий;С проведением разного числа параллельных испытаний в каждой точке плана, что однозначно усложняет расчеты, требуя учета разного числа m для своих строк;
С оценкой наличия взаимосвязей между параметрами, что требует расширения таблицы параметров с представлением всех возможных взаимосвязей и выполнения дальнейшего расчета. Данный план обычно получается насыщенным, но он позволяет выбрать наиболее подходящие параметры для перехода к дробным планам.
Слайд 42Дробный факторный эксперимент
Полный факторный эксперимент является удобным средством построения математической
модели исследуемого объекта особенно при числе факторов n>3, но увеличение
числа факторов приводит к резкому увеличению числа опытов. n=6 – N=64, n=7 – N=128. Конечно точность решений возрастает.Для получения достаточно точных оценок коэффициентов регрессии можно обойтись и меньшим количеством опытов, вводя понятие дробного факторного эксперимента (или дробных реплик).
Однако сокращение числа опытов влечет за собой появление корреляции между некоторыми столбцами матрицы планирования. Это обстоятельство не позволяет раздельно оценивать эффект факторов и их взаимосвязей. Возникают смешанные оценки.
Запись ДФЭ имеет вид 2n-p, где р – число дополнительных факторов, n – общее число факторов.
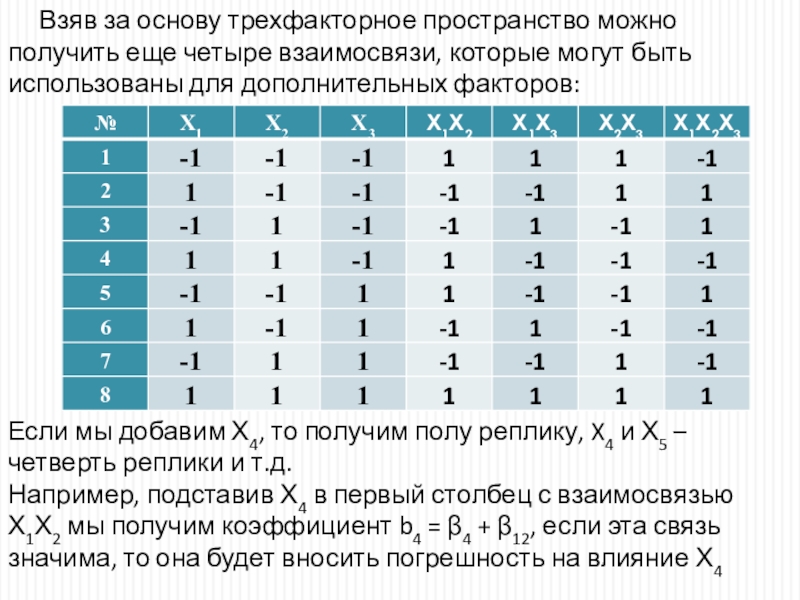
Слайд 43Взяв за основу трехфакторное пространство можно получить еще четыре взаимосвязи,
которые могут быть использованы для дополнительных факторов:
Если мы добавим Х4,
то получим полу реплику, X4 и Х5 – четверть реплики и т.д.Например, подставив Х4 в первый столбец с взаимосвязью Х1Х2 мы получим коэффициент b4 = β4 + β12, если эта связь значима, то она будет вносить погрешность на влияние Х4
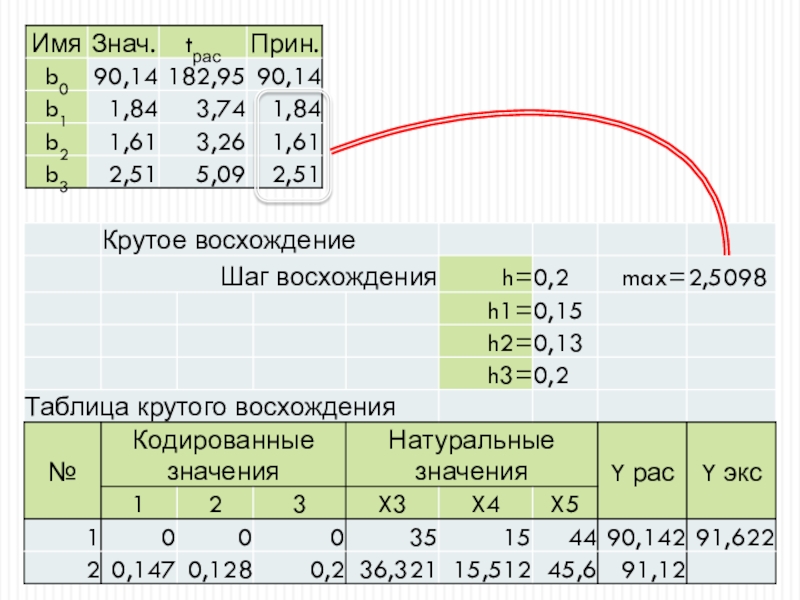
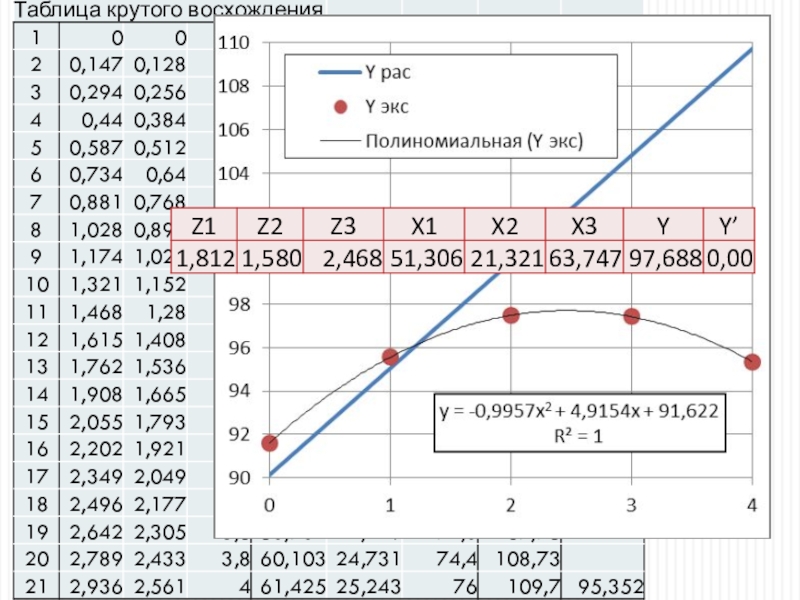
Слайд 44Крутое восхождение в область экстремума
Получив адекватную модель объекта, может реализовать
восхождение в область экстремума по градиенту.
Движение по градиенту предполагает наиболее
быстрый подъем вверх или спуск вниз. Градиент определяется производными по каждому входному параметру. Для пропорционального движения вдоль градиента обычно задается желаемый шаг, который задает перемещение к очередной точки по максимальной производной, по остальным параметрам шаг находится отношением значения производной по данному параметру к максимальной производной.Опорный шаг принимается в интервале от 0,1 до 0,5 в кодированных значениях. Начальная точка берется в центре ПФЭ. Через каждые 5-6 расчетных значений функции проводится экспериментальный её замер.
Слайд 47Центральные композиционные планы, общие положения
Задачами планов второго порядка являются проведение
оптимального плана исследований, получение нелинейной модели и ее статистический анализ.
Модель применяется для поиска координаты оптимума и может использоваться для целей интерполяции и экстраполяции.Построить данные планы с помощью ранее рассмотренных схем не удается потому, что нарушается условие ортогональности (сумма элементов столбцов не равна нулю). Требуется поставить большое число опытов (3n). Планирование на трех уровнях неэкономично и потому предложено дополнить план ПФЭ 2n определенными точками факторного пространства так, чтобы выполнялось условие ортогональности или ротатабельности, но при этом число опытов таких планов было меньшим, чем ПФЭ 3n :
N = 2n + 2n + N0 < 3n
Слайд 48Центральные композиционные планы, общие положения
Такие планы состоят из опытов ПФЭ
2n, «звездных» точек и опытов в центре плана. Большим преимуществом
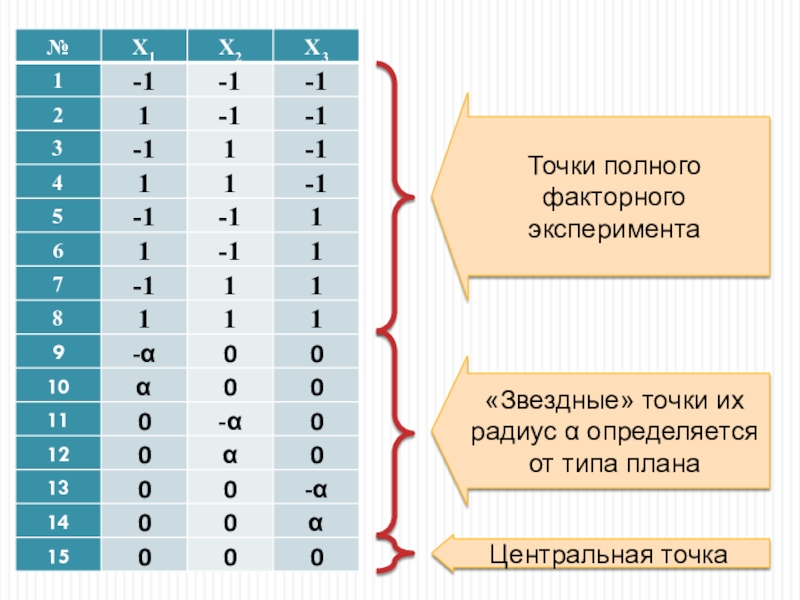
этих планов является то, что их можно получать из планов ПФЭ 2n. Для построения используется план 2n, линейная модель по которому при поиске области оптимума оказалась неадекватной. Все проведенные эксперименты остаются, а план дополняется определенным количеством специально подобранных «звездных» точек. Отметим, что дробная реплика предыдущего плана в новом плане дополняется до полного факторного эксперимента, если n≤4; при n>4 возможно использование дробных реплик. Эти планы называются центральными композиционными планами. Выбор плеча «звездных» точек и числа нулевых точек зависит от критерия оптимальности плана. В инженерной практике применяются ортогональные и ротатабельные планы второго порядка.Слайд 49Точки полного факторного эксперимента
«Звездные» точки их радиус α определяется от
типа плана
Центральная точка
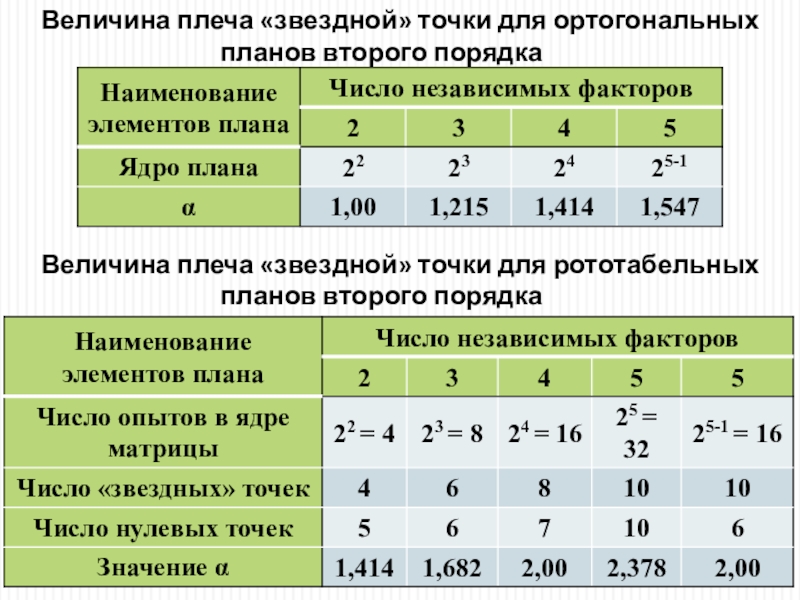
Слайд 50Величина плеча «звездной» точки для ортогональных планов второго порядка
Величина плеча
«звездной» точки для рототабельных планов второго порядка
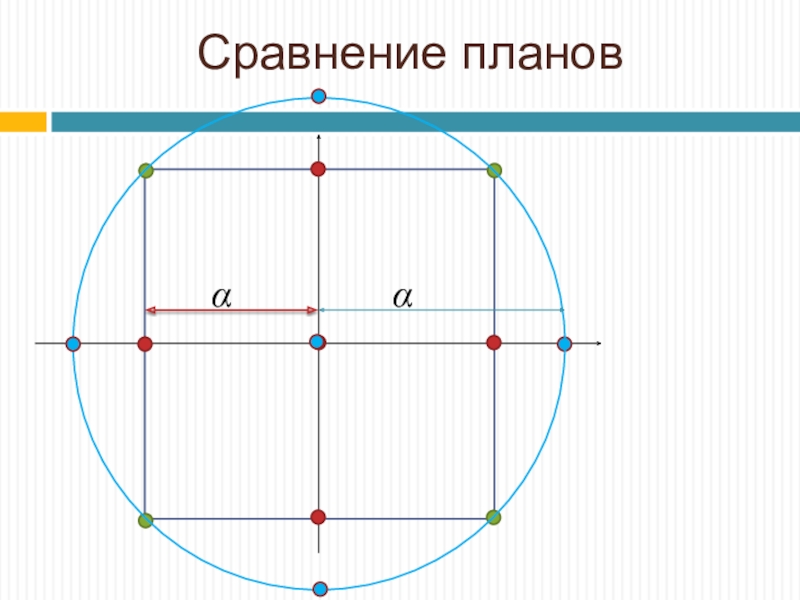
Слайд 52Методики расчетов ЦКП
Расчеты по результатам ЦКОП похожи на расчет ПФЭ,
но требуют дополнительных вычисления для нахождения коэффициентов при квадратах параметров
и при взаимосвязях. При проверке значимости коэффициентов их дисперсии имеют разные значения для всех видов коэффициентов (свободный член, линейные члены, взаимосвязи и квадратные члены).Расчеты по результатам ЦКРП существенно сложнее из-за их не ортогональности. При нахождении незначимых коэффициентов при членах второго порядка необходимо выполнять полный перерасчет результатов.
Если нелинейная модель, полученная по ЦКП, неадекватна, то возможны изменение порядка полинома (переход к полиному третьего порядка) или добавление новых факторов в уравнение регрессии или тщательный анализ ошибок в эксперименте.