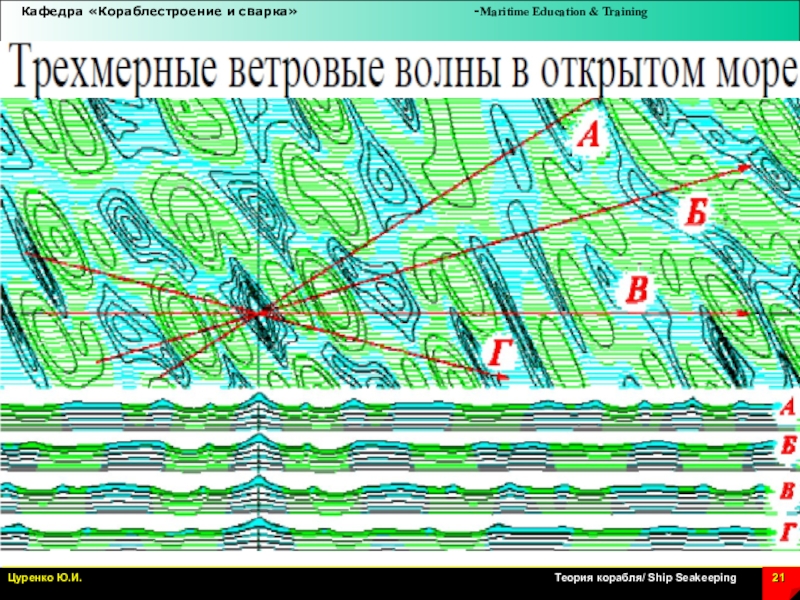
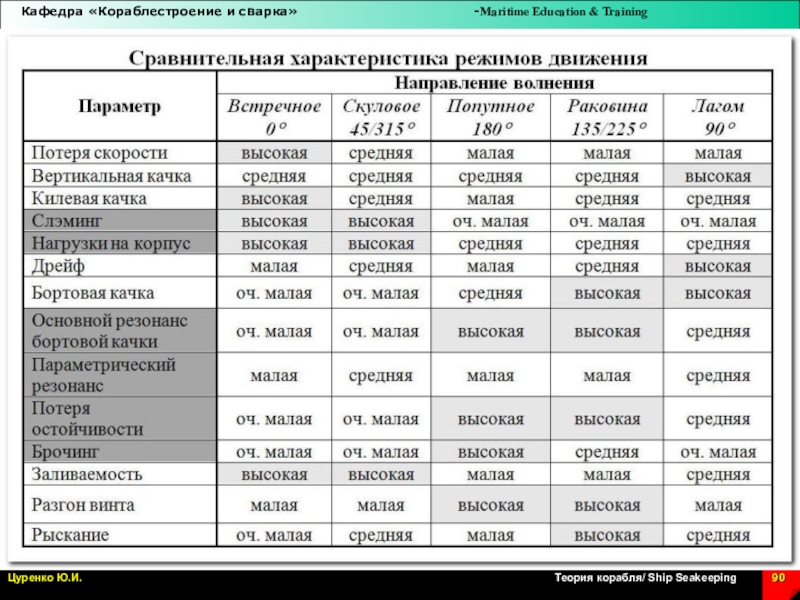
Слайд 2Мореходность судна - его способность эффективно противостоять действию волн и
ветра.
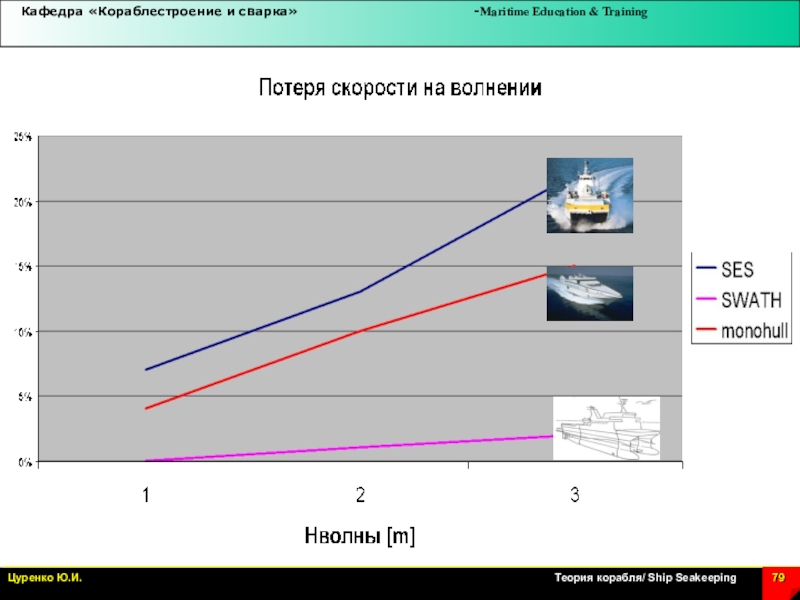
Определение скорости на волнении. В шторм скорость уменьшается из
- за дополнительного сопротивления при ходе на волнении. Если вследствие этого судно с недостаточным запасом мощности потеряет ход, оно может стать неуправляемым. Волны его развернут лагом и могут выбросить на мель или опрокинуть. С другой стороны, на волнении часто необходимо искусственное уменьшение скорости, чтобы избежать чрезмерной качки и ударов волн.
Безопасность судна в отношении опрокидывания, большой бортовой качки и ускорений, слеминга, ударов волн в корпус, надстройки или палубный груз, оголения гребного винта, приводящего к разносу и возможной поломке двигателя.
Слайд 3Определение волновых нагрузок и проектирование конструкций корпуса судна с их
учётом.
Обеспечение комфорта и безопасности людей на борту судна (морская болезнь,
опасность случайных падений людей, в том числе за борт).
Определение возможности проведения различных операций, например, промысловых, грузовых, швартовных, посадки вертолётов и др.
Оптимизация курса и маршрута перехода с учётом волнения, чтобы уменьшить, например, время рейса, расход топлива и др.
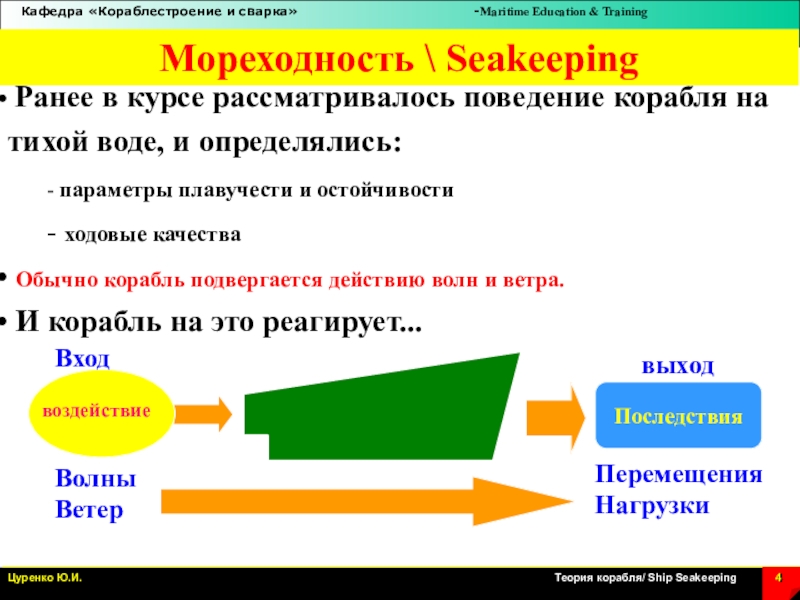
Слайд 4 Ранее в курсе рассматривалось поведение корабля на тихой воде,
и определялись:
- параметры плавучести и остойчивости
- ходовые качества
Обычно корабль подвергается действию волн и ветра.
И корабль на это реагирует...
воздействие
Волны
Ветер
Последствия
Вход
выход
Мореходность \ Seakeeping
Перемещения
Нагрузки
Слайд 5Волны \ Waves
Образование волн и Энергия волн
Передаваемая морю
энергия
Создание
волн
Скоростное судно
Большие
волны
Энергия волны, E= f(Высота волны²)
Удваиваем высоту
Учетверяем волновую энергию!
Cw (коэффициент волнового сопротивления) корпуса судна увеличивается при увеличении высоты создаваемых волн.
Слайд 6Волны \ Waves
Волны \ Waves
По происхождению, т. е. в зависимости
от сил, возбуждающих их, волны подразделяют на :
ветровые (волны трения)
Приливные
Анемобарические
сейсмические
(цунами)
корабельные
Слайд 7 Ветер генерирует волновую систему
Размеры волн в системе определяются:
Скоростью
ветра :
- Ветер большей скорости передает воде больше
энергии.
- Большие волны генерируются сильным ветром.
Направлением ветра :
- Чем дольше дует ветер в одном направлении, тем больше будет передано воде ветровой энергии .
Волны \ Waves
Слайд 8Waves
Волны \ Waves
Ветер генерирует волновую систему
Глубина водоема
- Высота волны зависит от глубины водоема.
- Волны
при выходе на пляж растут, заваливаются и разрушаются
Обдуваемая поверхность
- Поверхность воды, на которую действует ветер.
- Чем больше площадь этой поверхности, тем больше энергии передаст ветер морю.
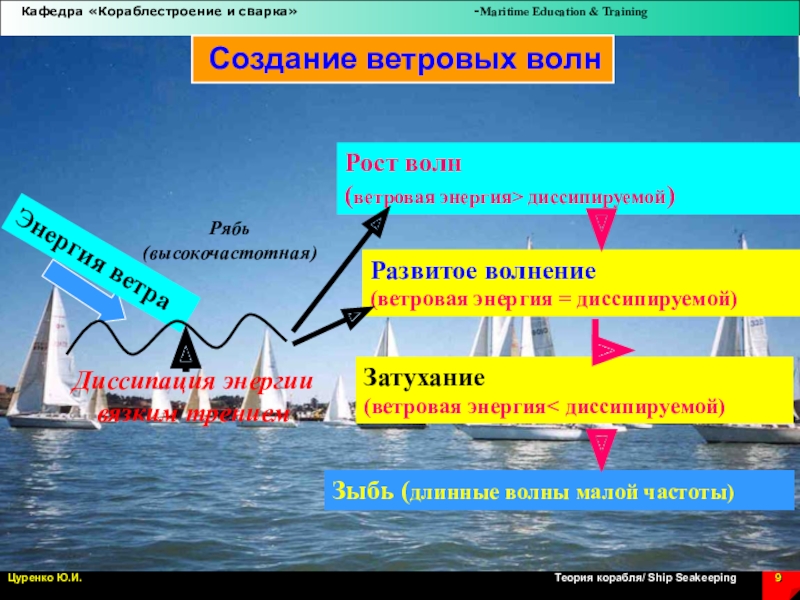
Слайд 9 Создание ветровых волн
Энергия ветра
Диссипация энергии
вязким трением
Развитое волнение
(ветровая энергия =
диссипируемой)
Зыбь (длинные волны малой частоты)
Рост волн
(ветровая энергия> диссипируемой)
Рябь
(высокочастотная)
Затухание
(ветровая энергия
диссипируемой)
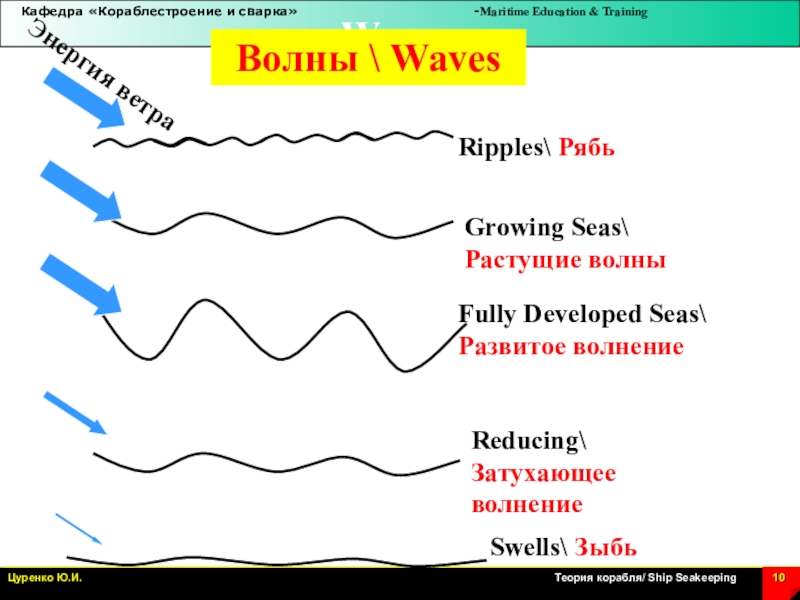
Слайд 10Энергия ветра
Ripples\ Рябь
Swells\ Зыбь
Growing Seas\ Растущие волны
Fully Developed Seas\ Развитое
волнение
Reducing\ Затухающее волнение
Waves
Волны \ Waves
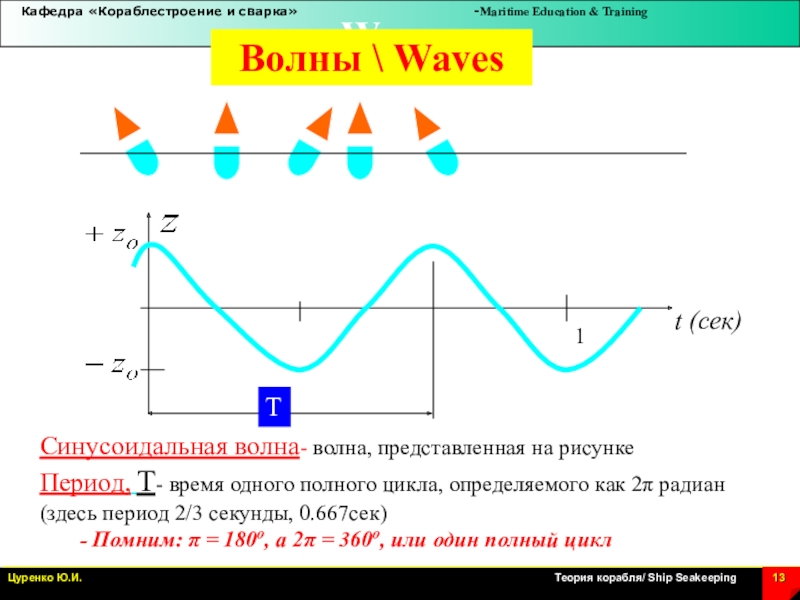
Слайд 13t (сек)
T
Синусоидальная волна- волна, представленная на рисунке
Период, T- время одного
полного цикла, определяемого как 2p радиан (здесь период 2/3 секунды,
0.667сек)
- Помним: p = 180o, а 2p = 360o, или один полный цикл
1
Waves
Волны \ Waves
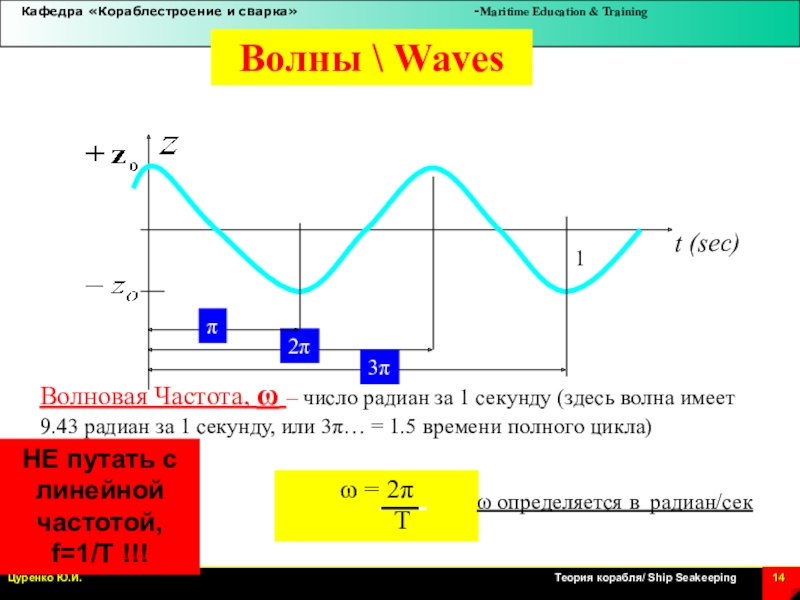
Слайд 14t (sec)
Волновая Частота, w – число радиан за 1 секунду
(здесь волна имеет 9.43 радиан за 1 секунду, или 3p…
= 1.5 времени полного цикла)
1
2p
p
3p
w определяется в радиан/сек
Волны \ Waves
НЕ путать с линейной частотой, f=1/T !!!
Слайд 15А вот две формулы для определения частоты собственных колебаний по
вертикали грузика массой m, подвешенного на пружине:
Где k = коэффициент
жесткости пружины (сила / длина при сжатии - растяжении)
Волны \ Waves
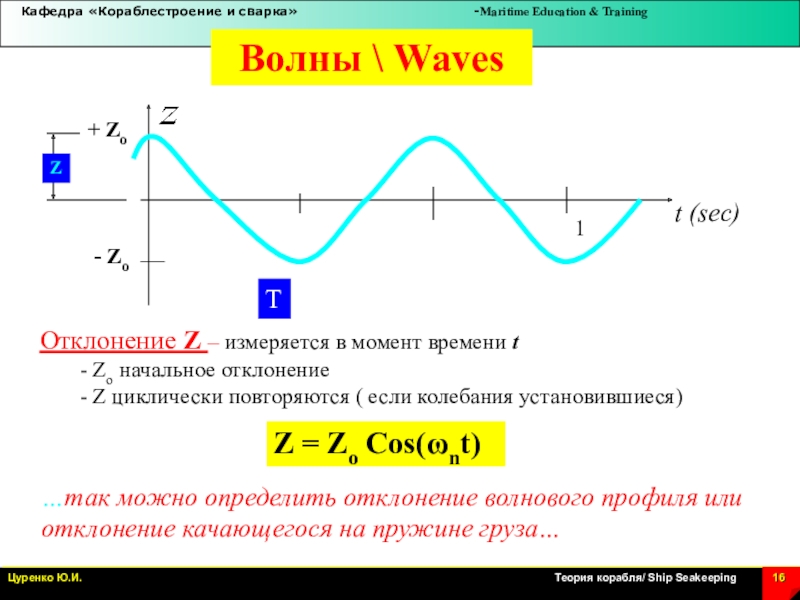
Слайд 16t (sec)
T
Отклонение Z – измеряется в момент времени t
- Zo
начальное отклонение
- Z циклически повторяются ( если колебания установившиеся)
1
…так можно
определить отклонение волнового профиля или отклонение качающегося на пружине груза…
Z = Zo Cos(wnt)
+ Zo
- Zo
Z
Волны \ Waves
Слайд 17Суперпозиция волн
Реальное волнение
«Расчетное» волнение
Слайд 18
Теорема суперпозиции
Реальная поверхность получается
в результате взаимодействия
различных волновых
систем.
(Нерегулярное волнение)
Любую волновую систему можно
представить суперпозицией многих
синусоидальных колебаний
различной
частоты, амплитуды и
направления.
Применяем спектральный
анализ ФУРЬЕ
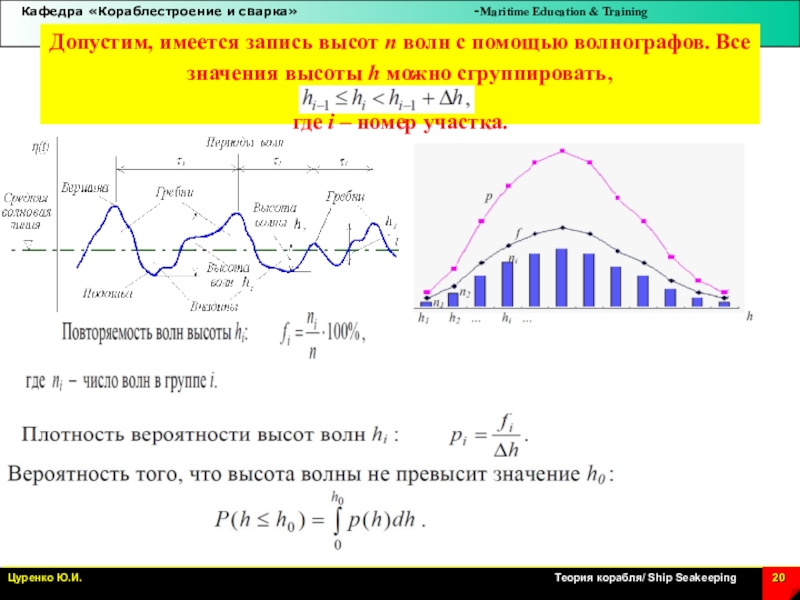
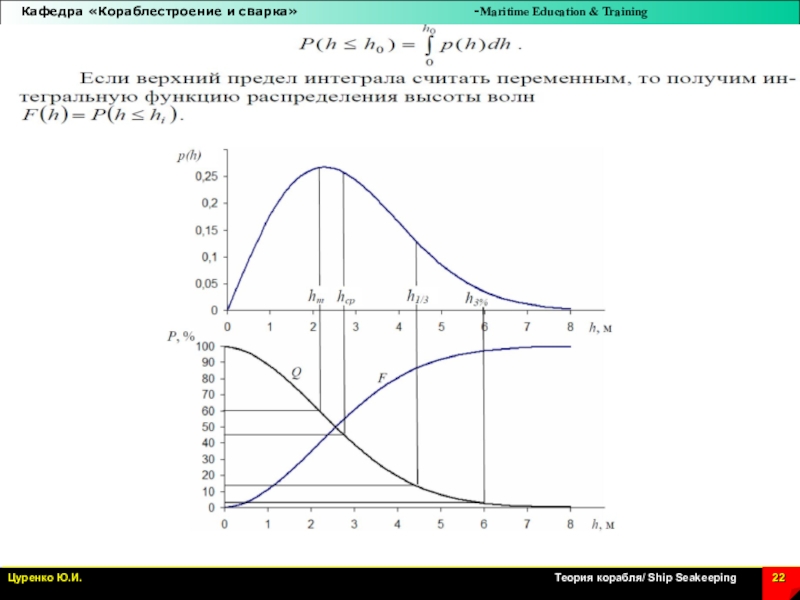
Слайд 20Допустим, имеется запись высот n волн с помощью волнографов. Все
значения высоты h можно сгруппировать,
где i – номер участка.
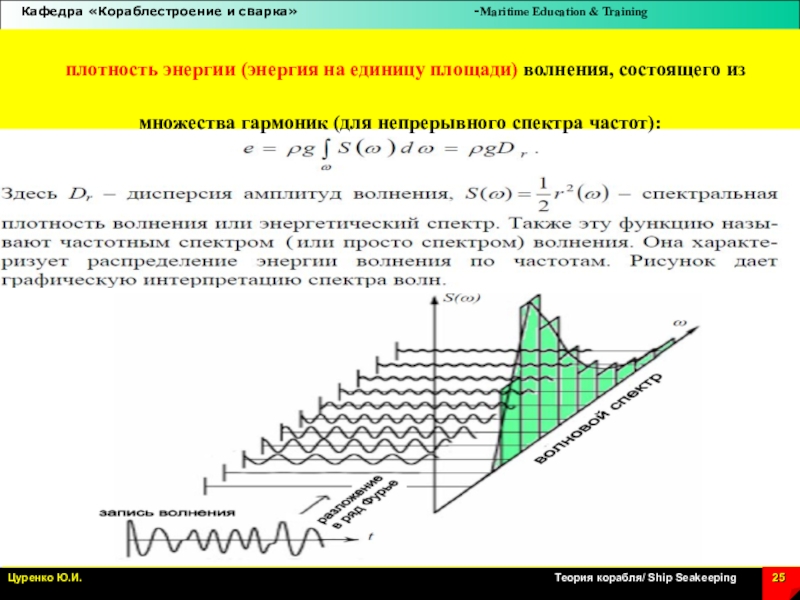
Слайд 25 плотность энергии (энергия на единицу площади) волнения, состоящего из
множества гармоник (для непрерывного спектра частот):
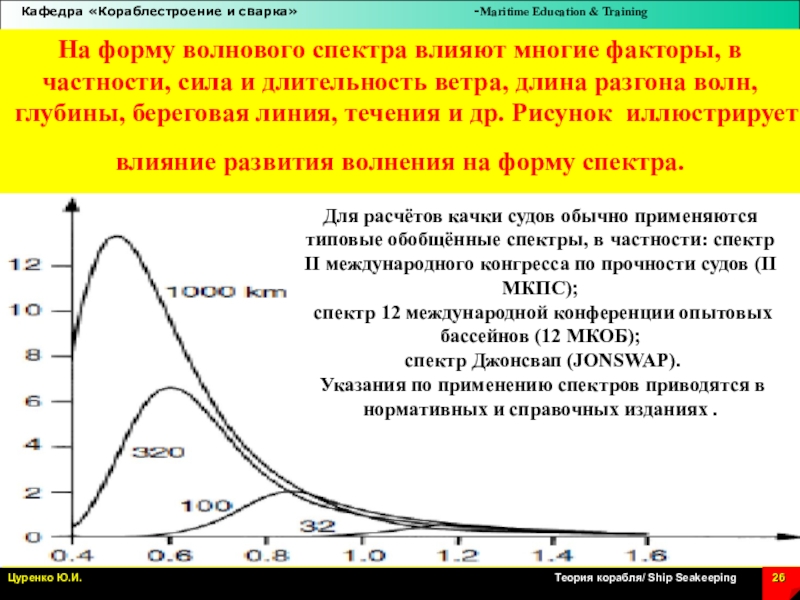
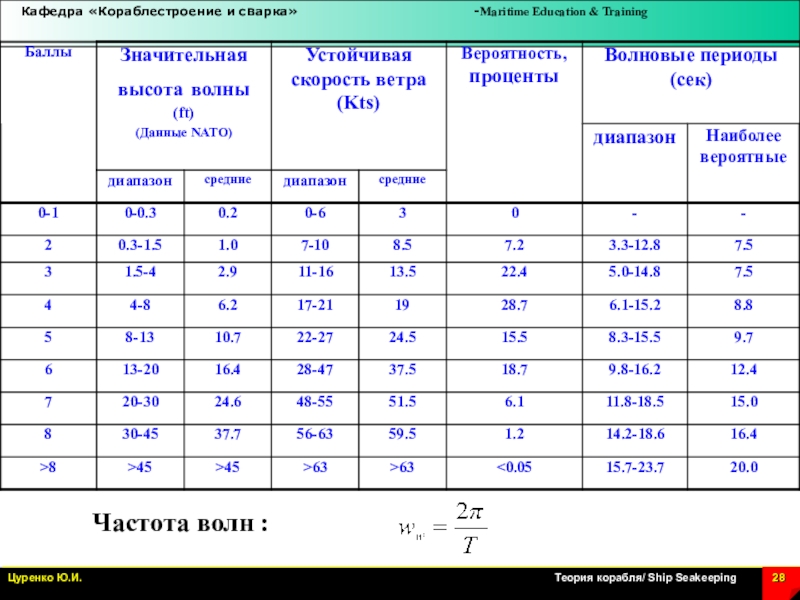
Слайд 26На форму волнового спектра влияют многие факторы, в частности, сила
и длительность ветра, длина разгона волн, глубины, береговая линия, течения
и др. Рисунок иллюстрирует влияние развития волнения на форму спектра.
Для расчётов качки судов обычно применяются типовые обобщённые спектры, в частности: спектр II международного конгресса по прочности судов (II МКПС);
спектр 12 международной конференции опытовых бассейнов (12 МКОБ);
спектр Джонсвап (JONSWAP).
Указания по применению спектров приводятся в нормативных и справочных изданиях .
Слайд 27
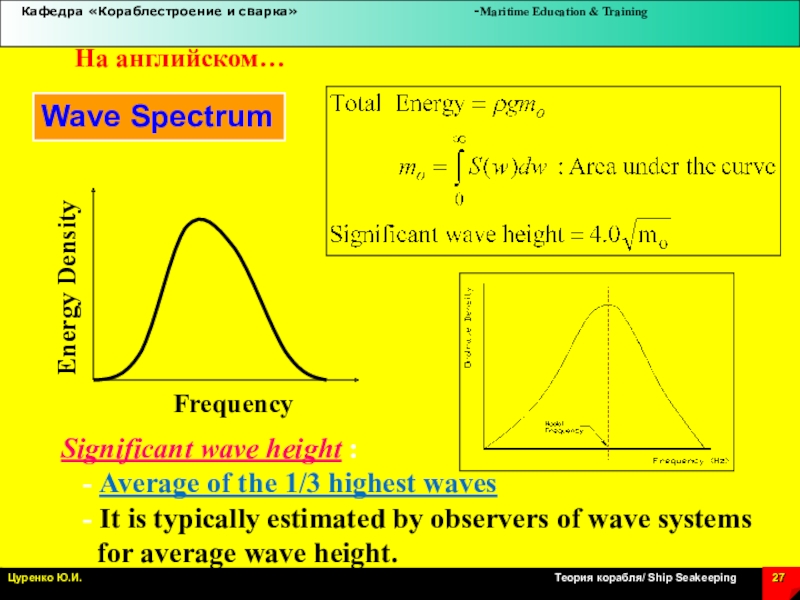
Wave Spectrum
Frequency
Energy Density
Significant wave height :
-
Average of the 1/3 highest waves
- It is
typically estimated by observers of wave systems
for average wave height.
На английском…
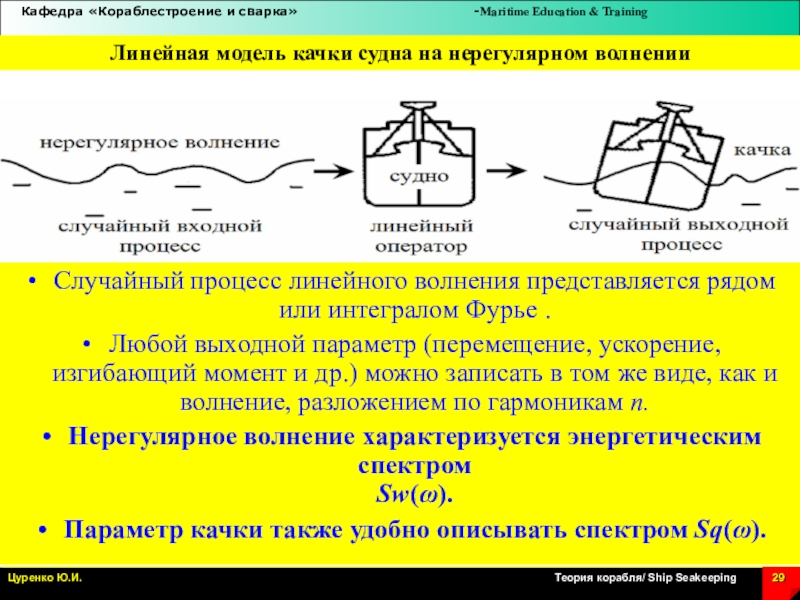
Слайд 29Случайный процесс линейного волнения представляется рядом или интегралом Фурье .
Любой выходной параметр (перемещение, ускорение, изгибающий момент и др.) можно
записать в том же виде, как и волнение, разложением по гармоникам n.
Нерегулярное волнение характеризуется энергетическим спектром
Sw(ω).
Параметр качки также удобно описывать спектром Sq(ω).
Линейная модель качки судна на нерегулярном волнении
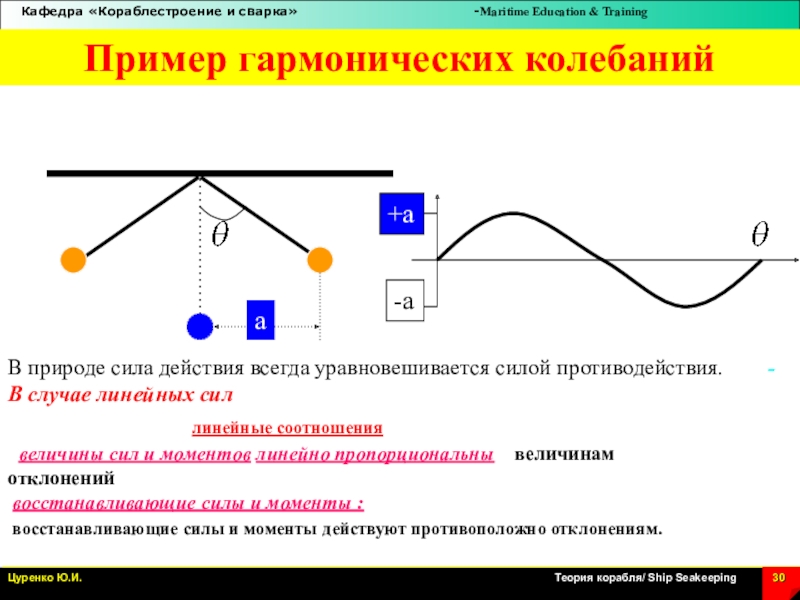
Слайд 30Пример гармонических колебаний
линейные соотношения :
величины сил и моментов
линейно пропорциональны величинам
отклонений
восстанавливающие силы и моменты
:
восстанавливающие силы и моменты действуют противоположно отклонениям.
a
В природе сила действия всегда уравновешивается силой противодействия. - В случае линейных сил
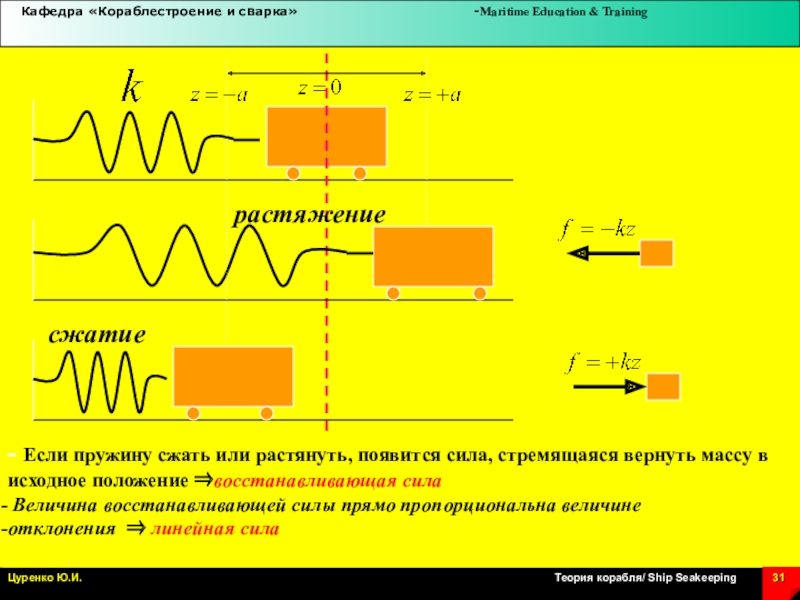
Слайд 31растяжение
сжатие
- Если пружину сжать или растянуть, появится сила, стремящаяся вернуть
массу в исходное положение восстанавливающая сила
Величина восстанавливающей силы прямо
пропорциональна величине
отклонения линейная сила
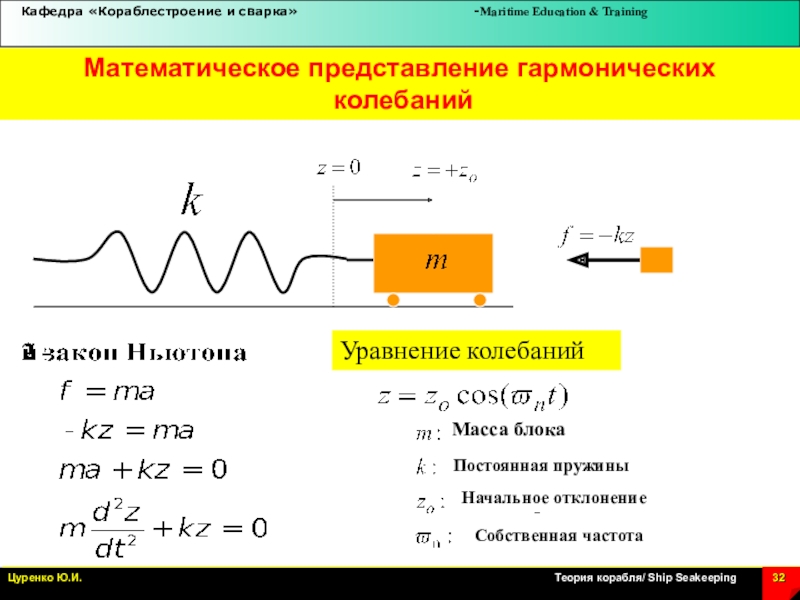
Слайд 32Математическое представление гармонических
колебаний
Уравнение колебаний
Масса блока
Постоянная пружины
Начальное отклонение
Собственная частота
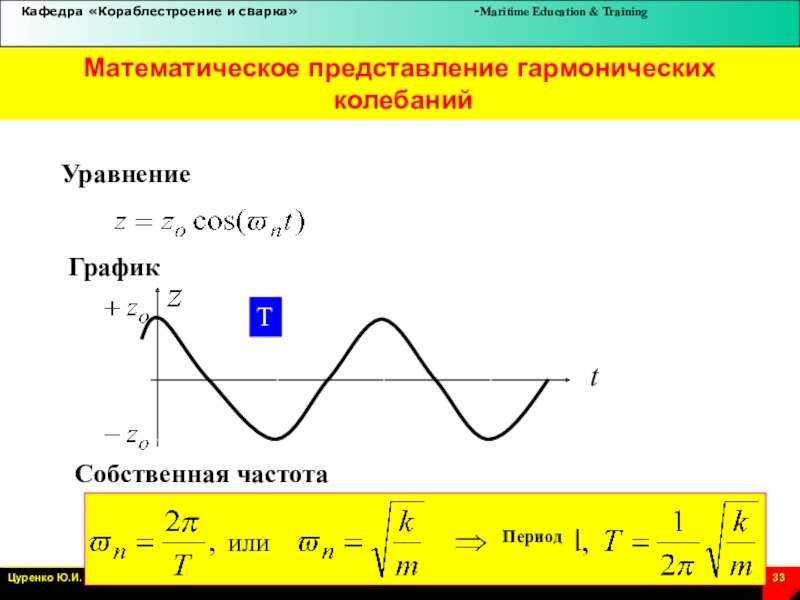
Слайд 33Уравнение
График
t
T
Собственная частота
Математическое представление гармонических
колебаний
Период
или
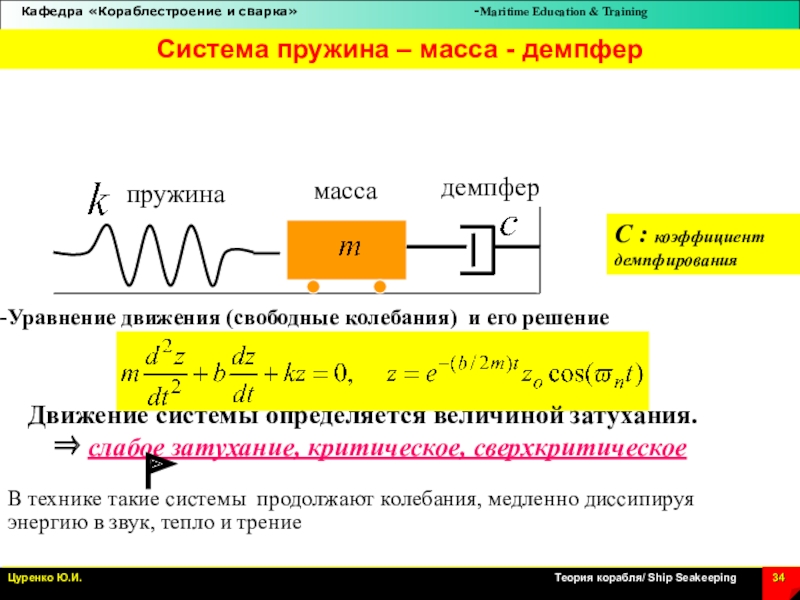
Слайд 34Система пружина – масса - демпфер
пружина
масса
демпфер
Уравнение движения (свободные колебания) и
его решение
C : коэффициент
демпфирования
Движение системы определяется величиной затухания.
слабое затухание, критическое, сверхкритическое
В технике такие системы продолжают колебания, медленно диссипируя энергию в звук, тепло и трение
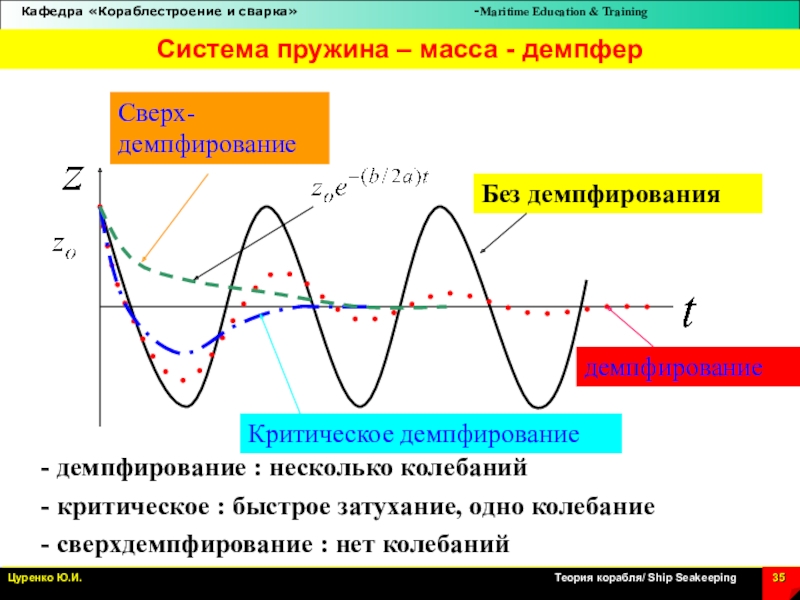
Слайд 35- демпфирование : несколько колебаний
- критическое : быстрое затухание, одно
колебание
- сверхдемпфирование : нет колебаний
Без демпфирования
демпфирование
Критическое демпфирование
Сверх-
демпфирование
Система пружина – масса
- демпфер
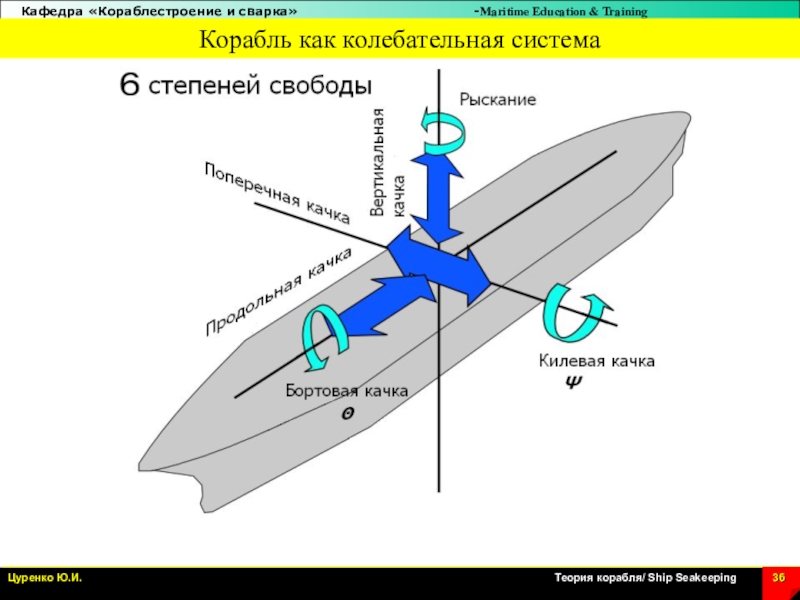
Слайд 36Корабль как колебательная система
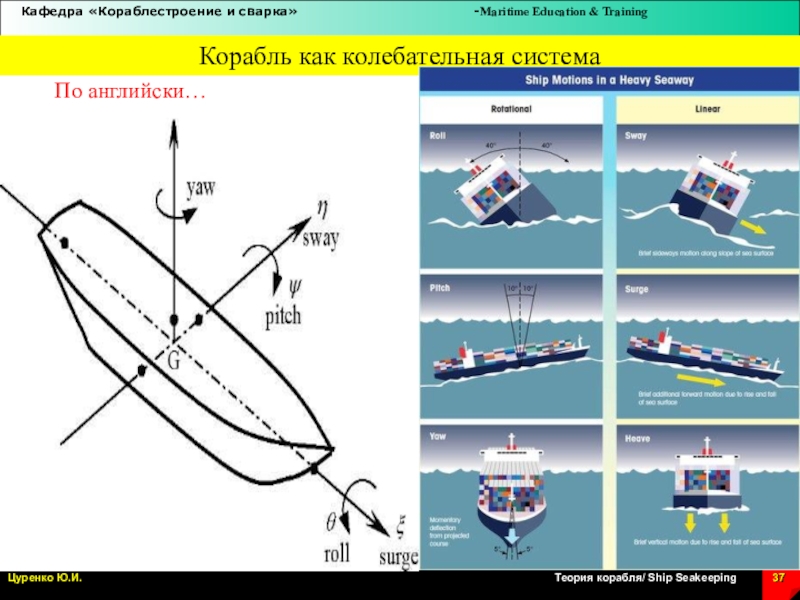
Слайд 37Корабль как колебательная система
По английски…
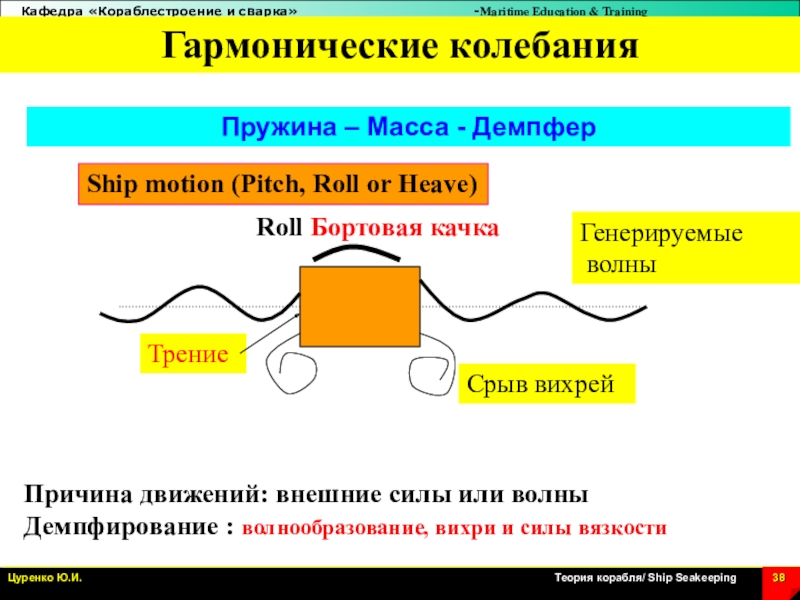
Слайд 38Пружина – Масса - Демпфер
Roll Бортовая качка
Причина движений: внешние силы
или волны
Демпфирование : волнообразование, вихри и силы вязкости
Генерируемые
волны
Срыв
вихрей
Трение
Ship motion (Pitch, Roll or Heave)
Гармонические колебания
Слайд 39Внешние силы и резонанс
Если энергия не пополняется,
система приходит в
состояние покоя
Внешние силы могут:
Гасить колебания
Усиливать колебания
Внешние силы,
действующие с частотой
собственных колебаний системы,
могут приводить к РЕЗОНАНСУ!
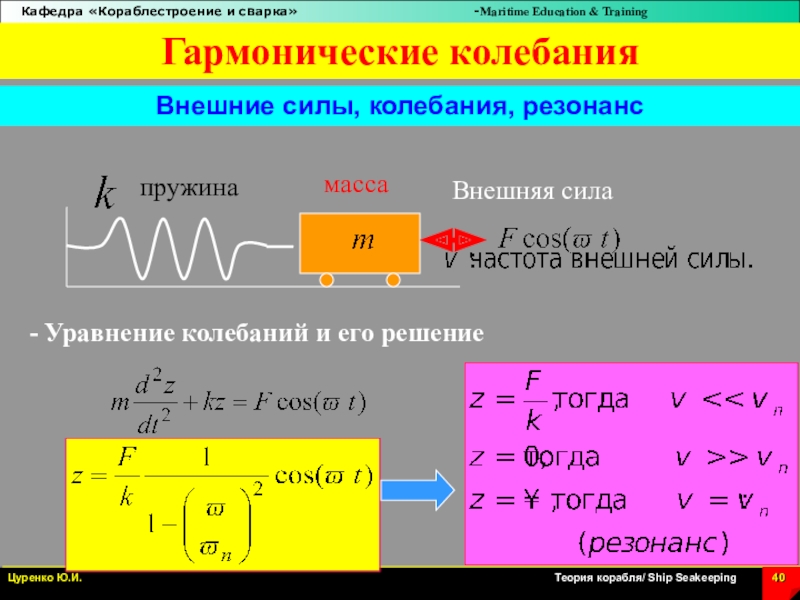
Слайд 40Внешние силы, колебания, резонанс
пружина
масса
- Уравнение колебаний и его решение
Внешняя сила
Гармонические
колебания
Слайд 41Уравнение движения
Амплитуда вынужденных колебаний
b : коэффициент
демпфирования
Simple Harmonic Motion
Гармонические колебания
Внешние силы,
колебания, демпфирование и резонанс
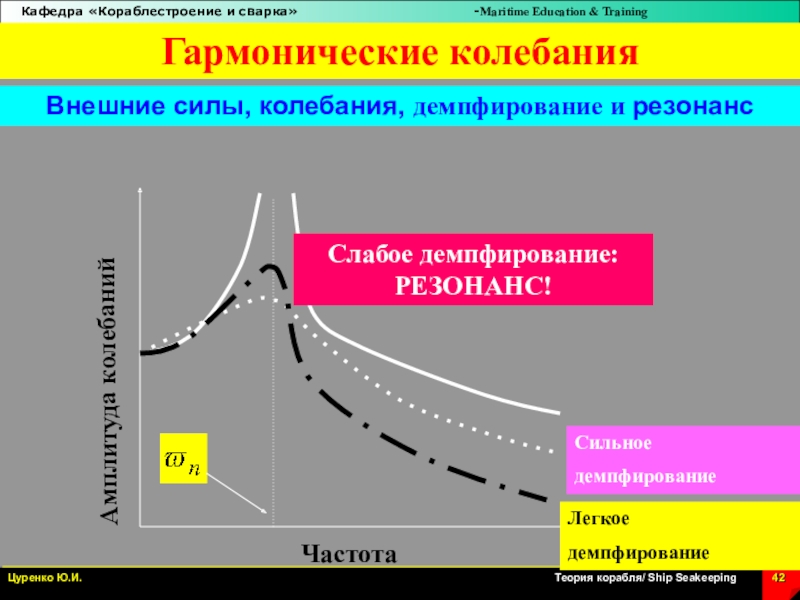
Слайд 42Частота
Амплитуда колебаний
Слабое демпфирование:
РЕЗОНАНС!
Легкое
демпфирование
Сильное
демпфирование
Гармонические колебания
Внешние силы, колебания, демпфирование и
резонанс
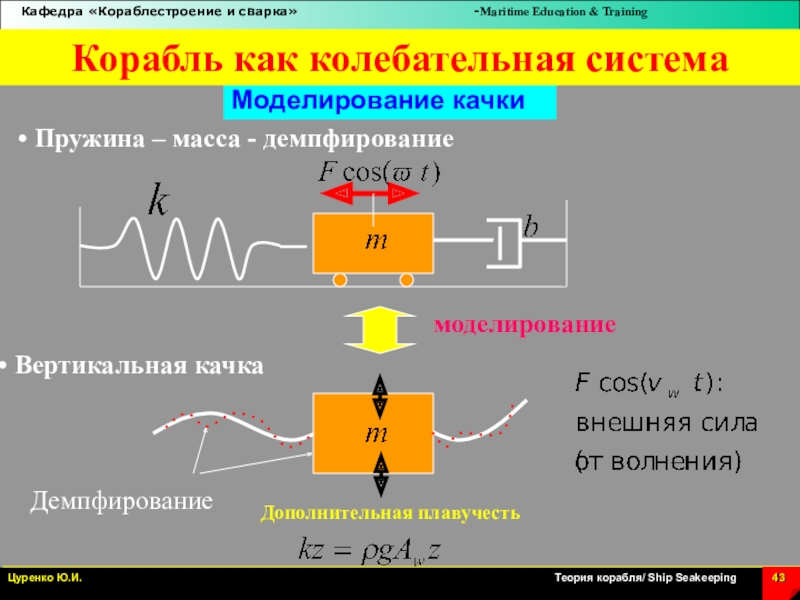
Слайд 43Моделирование качки
Корабль как колебательная система
Вертикальная качка
Демпфирование
Пружина – масса
- демпфирование
моделирование
Дополнительная плавучесть
Слайд 44Вынужденные колебания
Движения, создаваемые в системе определяются
амплитудой внешней силы
(F) и ее частотой (w).
Колебания судна на волнении
описываются как и в
системе Пружина – масса - демпфер.
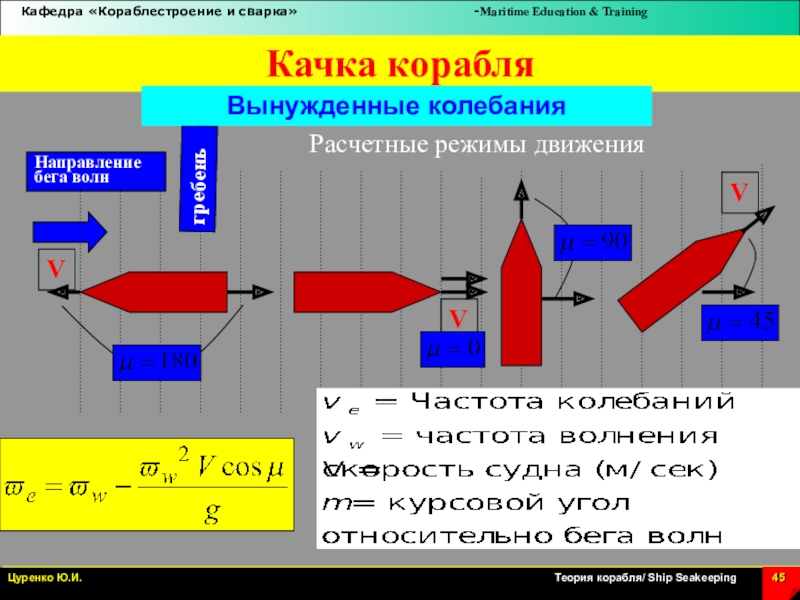
Частота внешних сил зависит от частоты волнения, скорости хода и направления движения судна.
Качка корабля
Слайд 45Качка корабля
Вынужденные колебания
Расчетные режимы движения
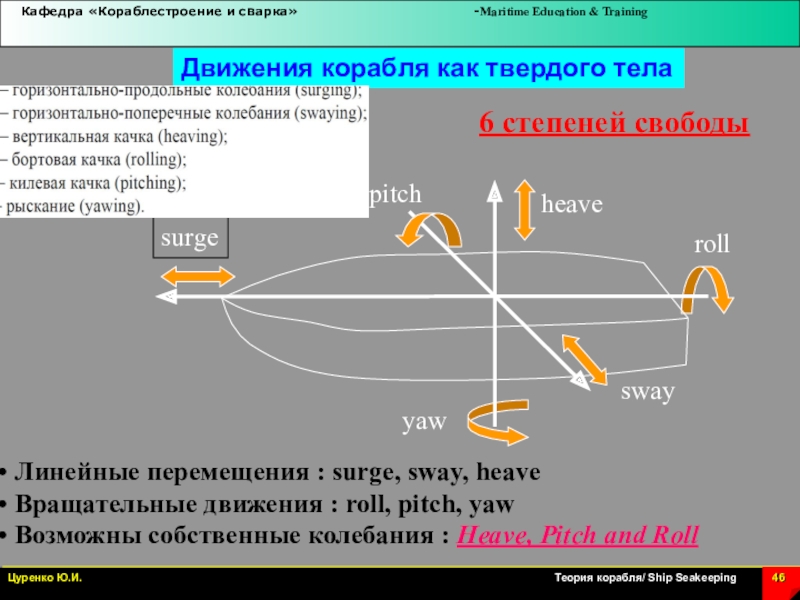
Слайд 46Движения корабля как твердого тела
Линейные перемещения : surge, sway,
heave
Вращательные движения : roll, pitch, yaw
Возможны собственные
колебания : Heave, Pitch and Roll
6 степеней свободы
Слайд 47Вертикальная качка
Восстанавливающие силы при вертикальных перемещениях
z
z
= F
B
Корабль в покое
DWL
результирующая
сила
F
B
>
DWL
Результир.
сила
C
L
C
L
C
L
•
•
B
G
•
•
G
B
•
•
G
B
> F
B
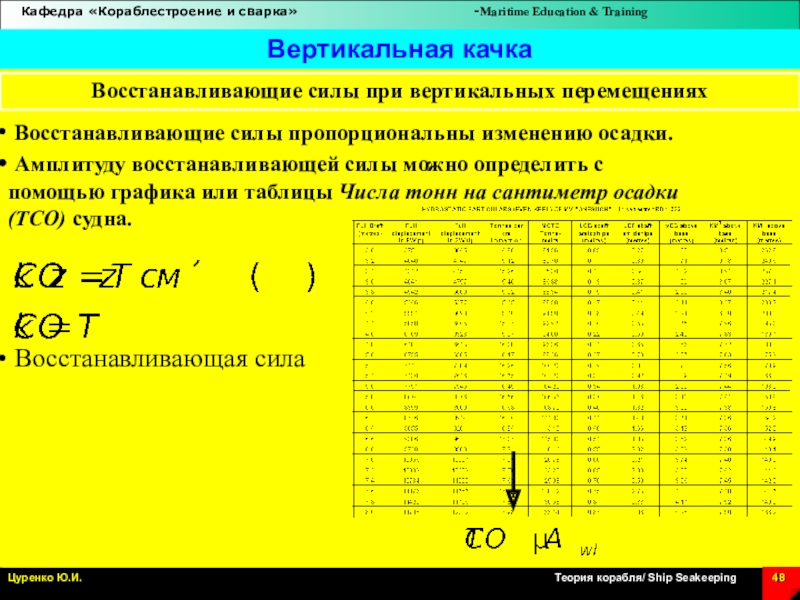
Слайд 48 Восстанавливающие силы пропорциональны изменению осадки.
Амплитуду восстанавливающей силы можно
определить с
помощью графика или таблицы Числа тонн на сантиметр
осадки
(ТСО) судна.
Восстанавливающая сила
Вертикальная качка
Восстанавливающие силы при вертикальных перемещениях
Слайд 49 : Частота собственных вертикальных
колебаний системы масса – пружина
Heave Natural frequency
Частота собственных вертикальных колебаний
Ship Response
Вертикальная качка
Здесь водоизмещение
и массу нужно увеличить на величину «ПРИСОЕДИНЕННОЙ МАССЫ» !!!
Слайд 50Простые приближенные формулы
для периодов вертикальной и килевой качки
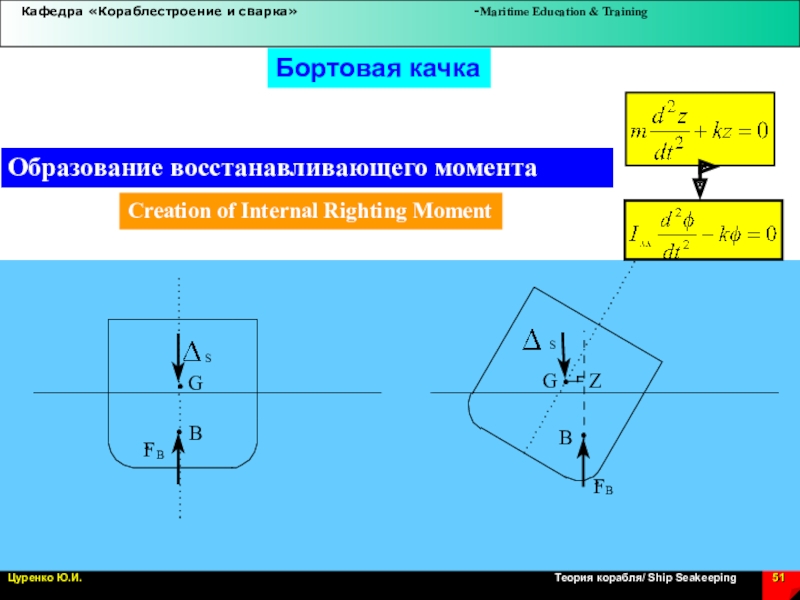
Слайд 51Бортовая качка
Образование восстанавливающего момента
Creation of Internal Righting Moment
G
S
B
F
B
¸
B
F
B
¸
G
Z
S
•
•
•
•
Слайд 52Простая приближенная формула
для периода бортовой качки
Бортовая качка затухает медленнее,
чем вертикальная
и килевая!!!
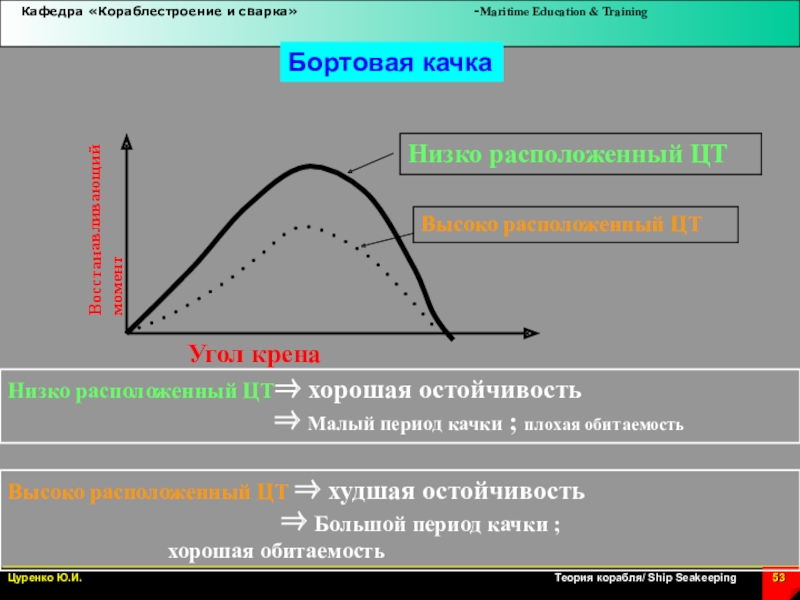
Слайд 53Бортовая качка
Низко расположенный ЦТ хорошая остойчивость
Малый период качки ; плохая обитаемость
Высоко расположенный ЦТ худшая остойчивость
Большой период качки ;
хорошая обитаемость
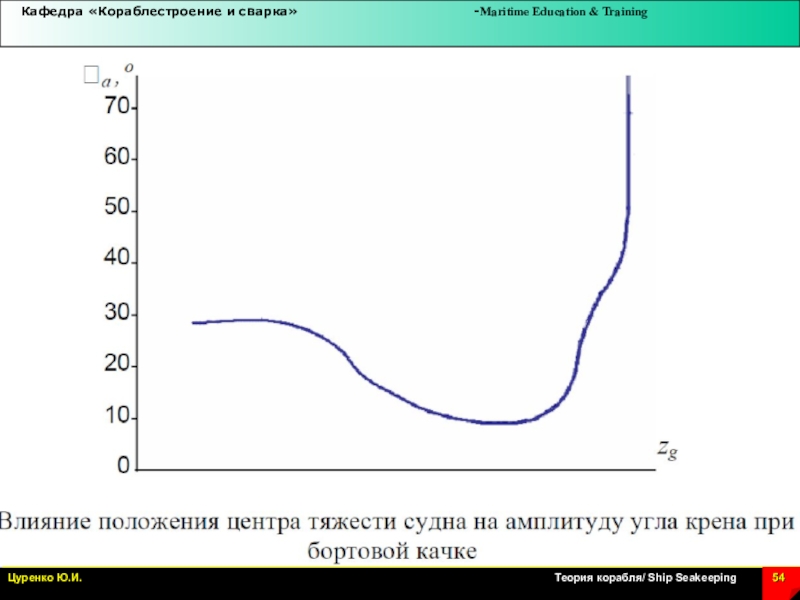
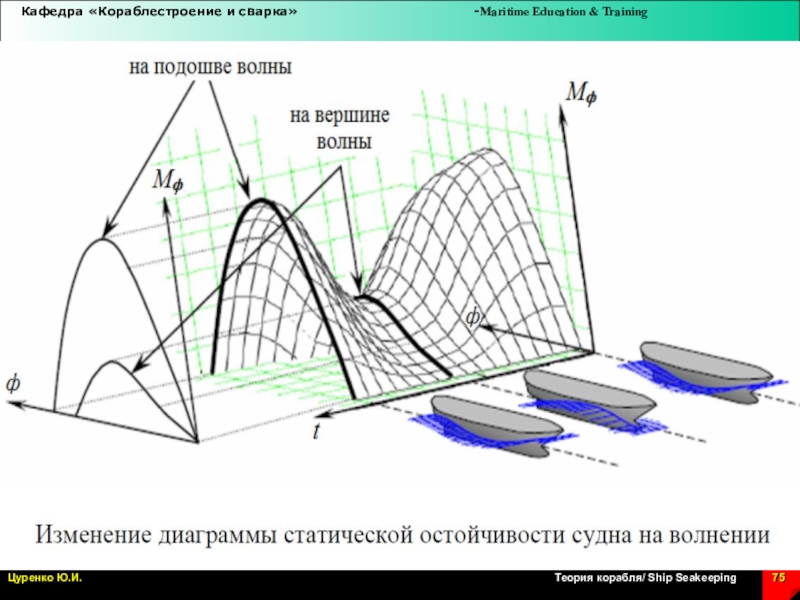
Слайд 55Остойчивость судна в условиях совместного действия волнения и ветра
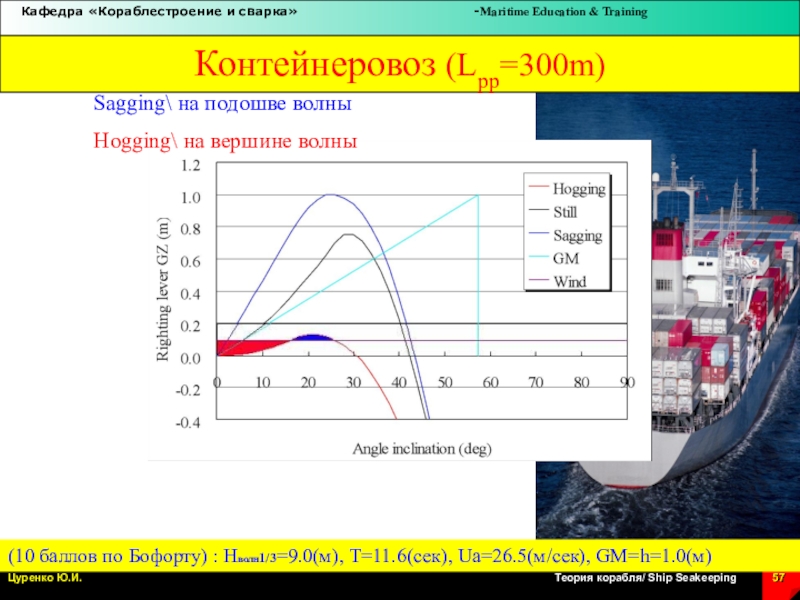
Слайд 57Контейнеровоз (Lpp=300m)
(10 баллов по Бофорту) : Hволн1/3=9.0(м), T=11.6(сек), Ua=26.5(м/сек), GM=h=1.0(м)
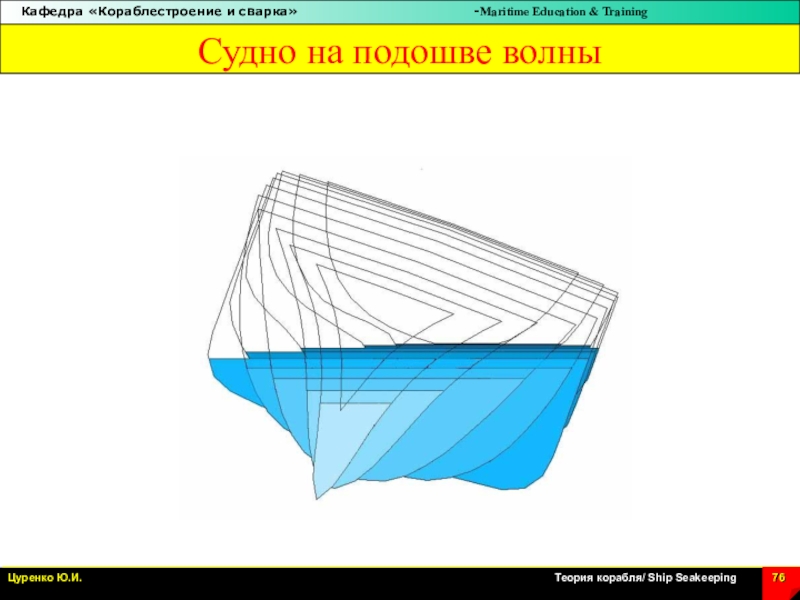
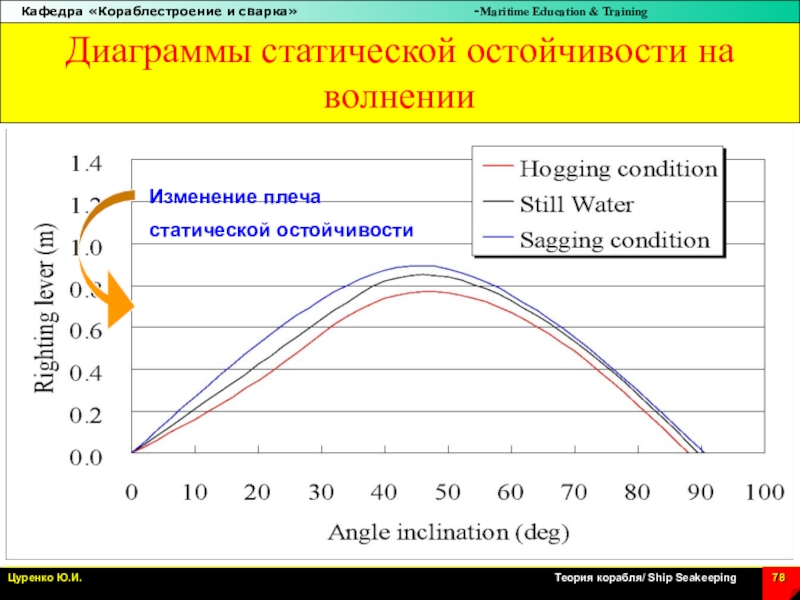
Sagging\
на подошве волны
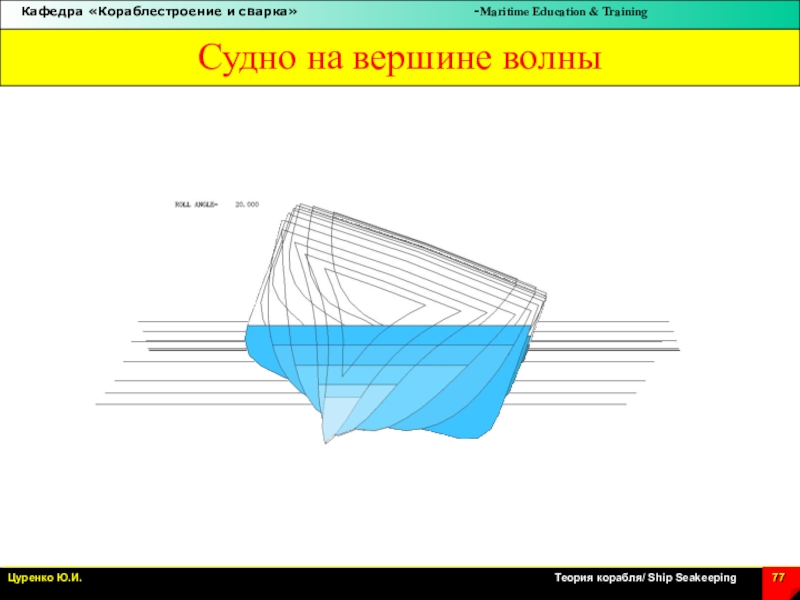
Hogging\ на вершине волны
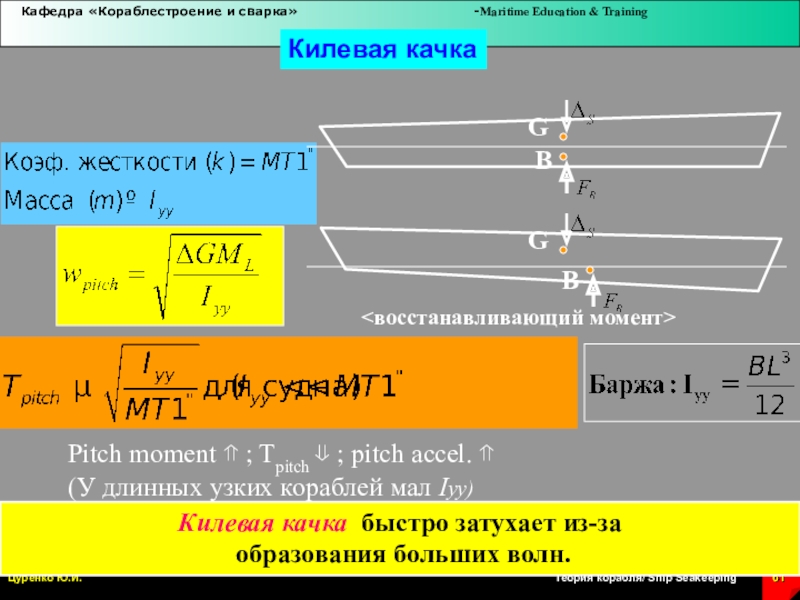
Слайд 61Килевая качка
(У длинных узких кораблей мал Iyy)
Килевая качка быстро затухает
из-за
образования больших волн.
G
B
Pitch moment ; Tpitch
; pitch accel.
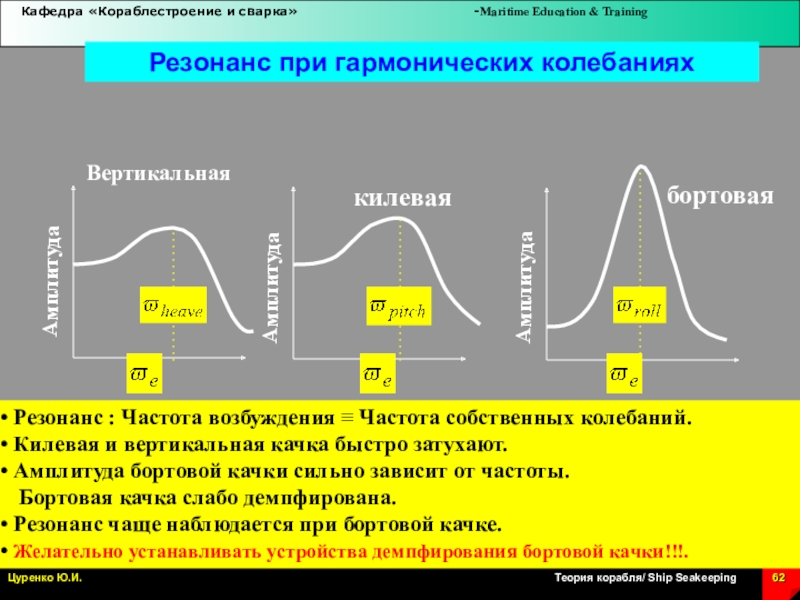
Слайд 62Резонанс при гармонических колебаниях
Вертикальная
килевая
бортовая
Амплитуда
Амплитуда
Амплитуда
Резонанс : Частота возбуждения Частота
собственных колебаний.
Килевая и вертикальная качка быстро затухают.
Амплитуда бортовой
качки сильно зависит от частоты.
Бортовая качка слабо демпфирована.
Резонанс чаще наблюдается при бортовой качке.
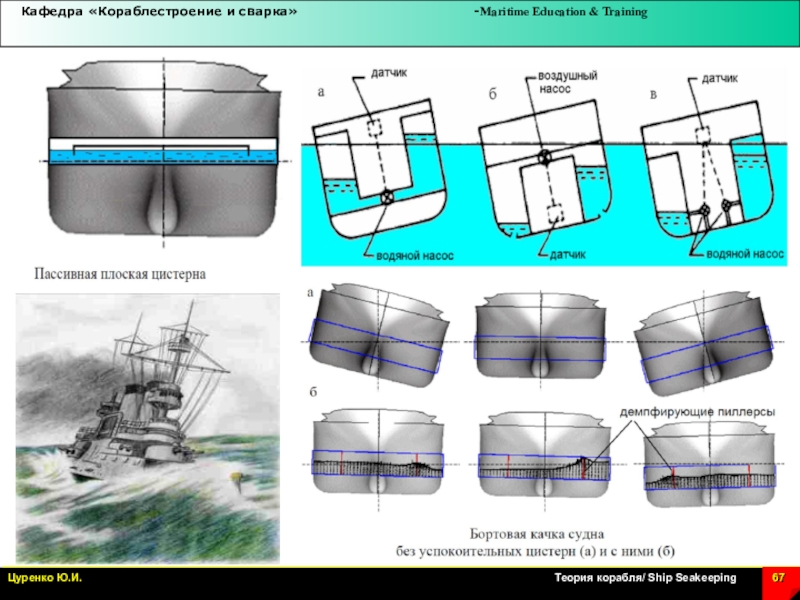
Желательно устанавливать устройства демпфирования бортовой качки!!!.
Слайд 63Пароход Бессемера
Пассажирский салон (21х9 метров) парохода был подвешен на продольной
оси. Матрос, поглядывая на спиртовой уровень, с помощью гидравлических машин
должен был выравнивать салон и компенсировать таким образом наклон судна. Помимо этого, салон соединялся с корпусом через резиновые амортизаторы для уменьшения вибраций и ударов.
Слайд 77Судно на вершине волны
Hogging condition (Crest condition)
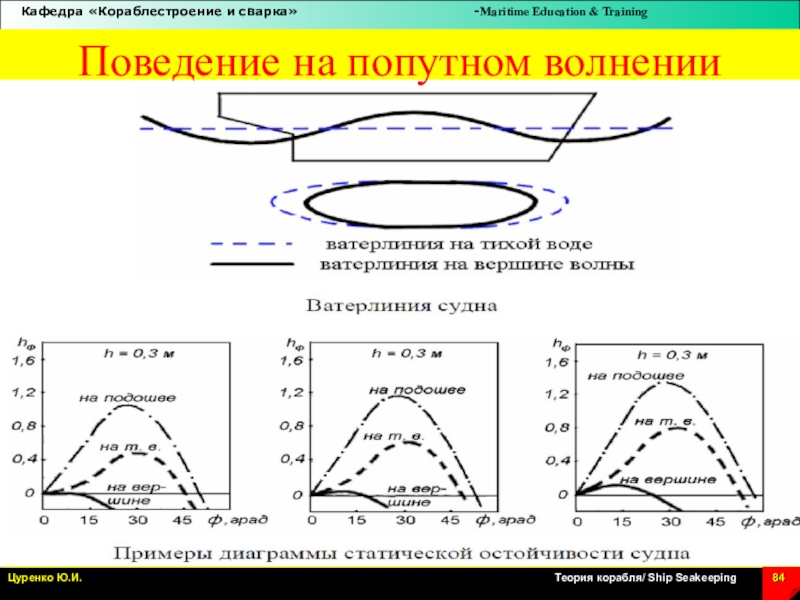
Слайд 78Диаграммы статической остойчивости на волнении
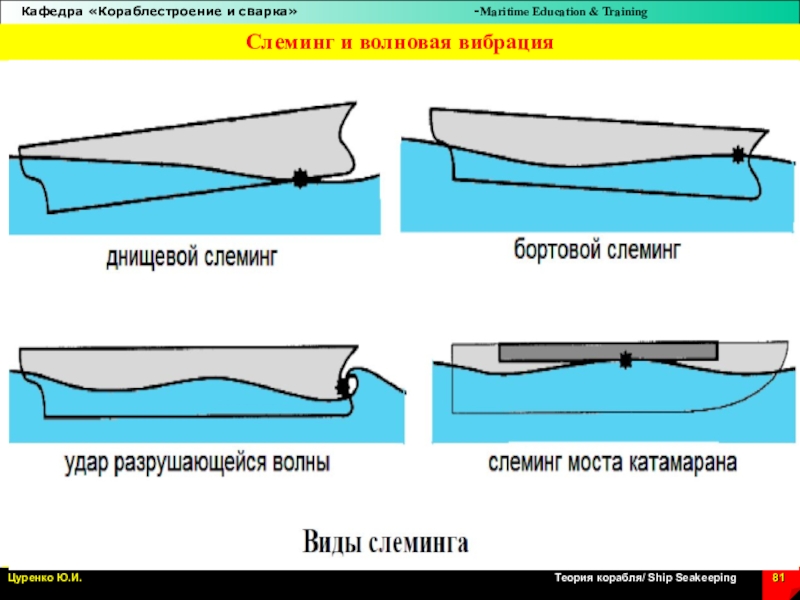
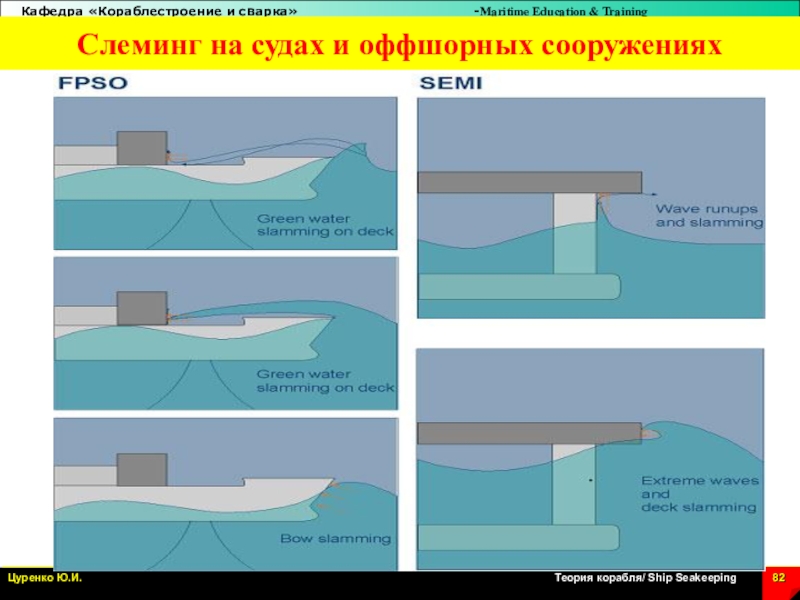
Слайд 82Слеминг на судах и оффшорных сооружениях
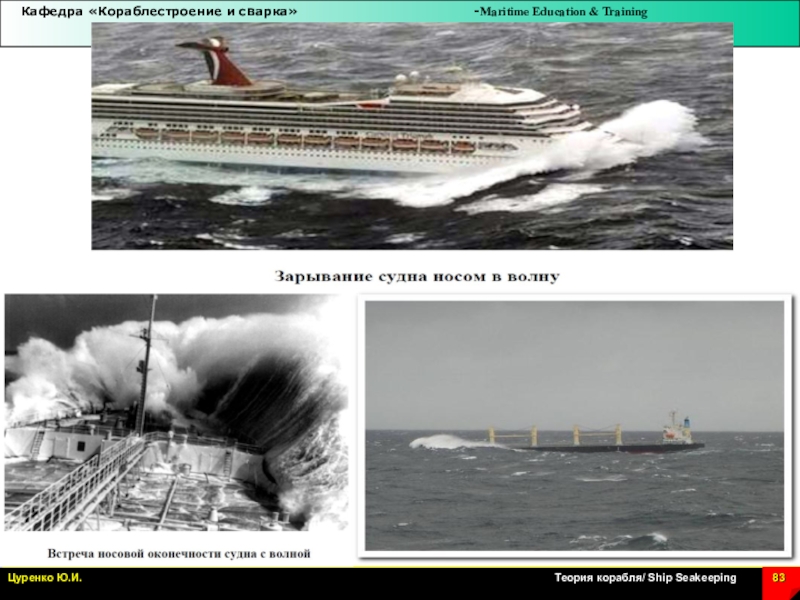
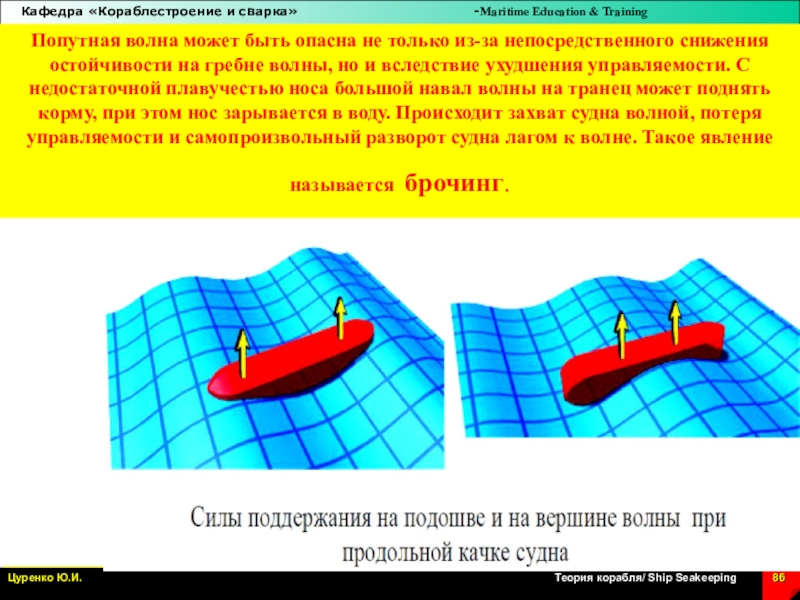
Слайд 86Попутная волна может быть опасна не только из-за непосредственного снижения
остойчивости на гребне волны, но и вследствие ухудшения управляемости. С
недостаточной плавучестью носа большой навал волны на транец может поднять корму, при этом нос зарывается в воду. Происходит захват судна волной, потеря управляемости и самопроизвольный разворот судна лагом к волне. Такое явление называется брочинг.