Начертательная геометрия

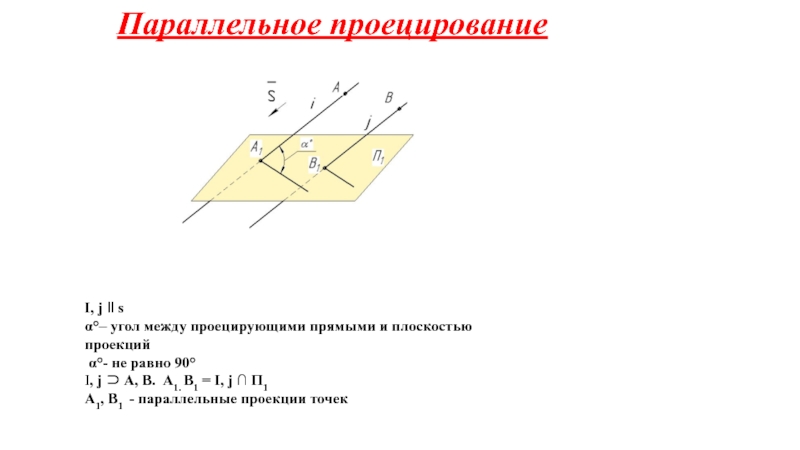
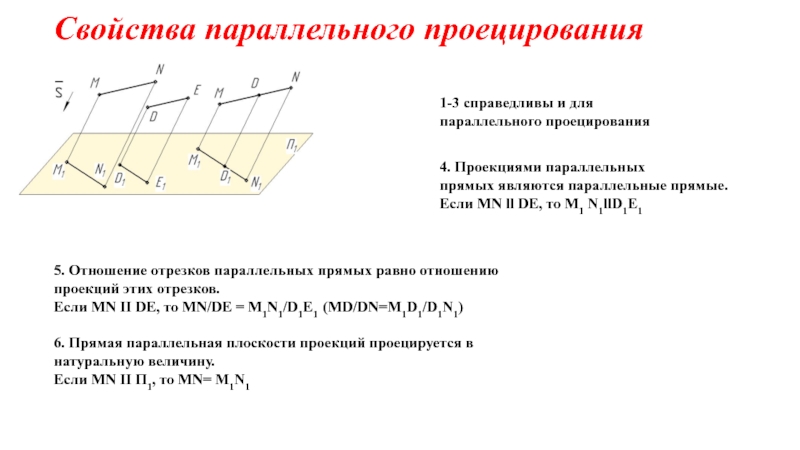
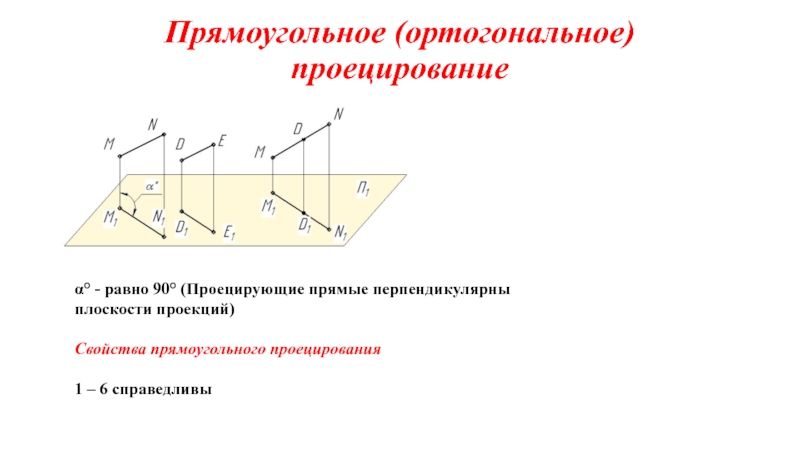
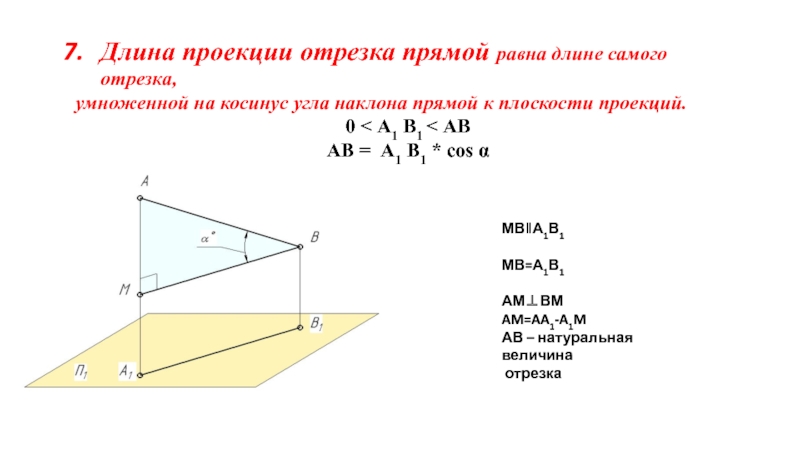
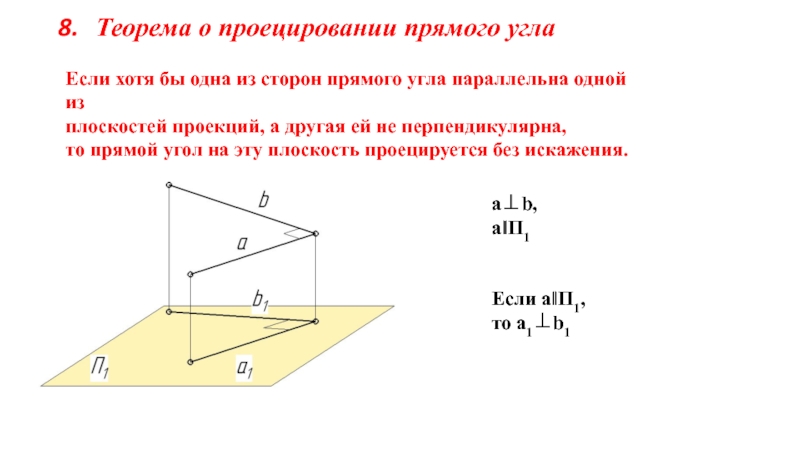
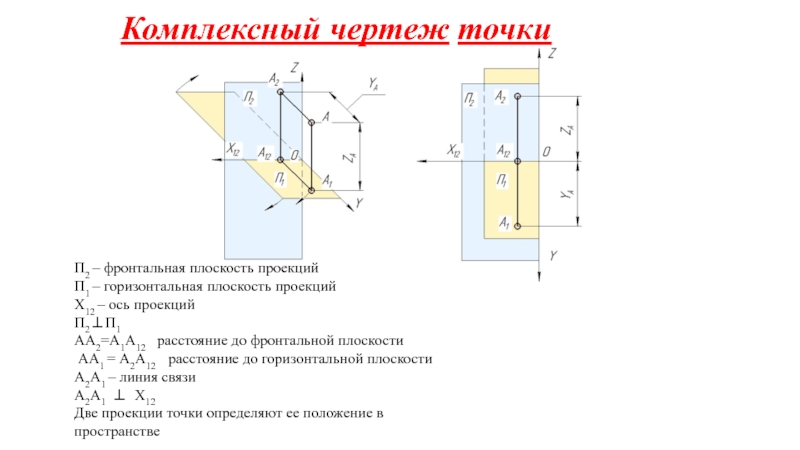
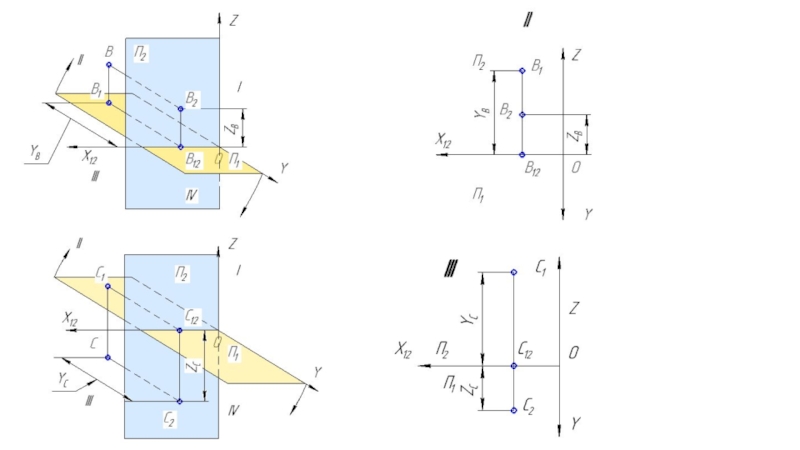
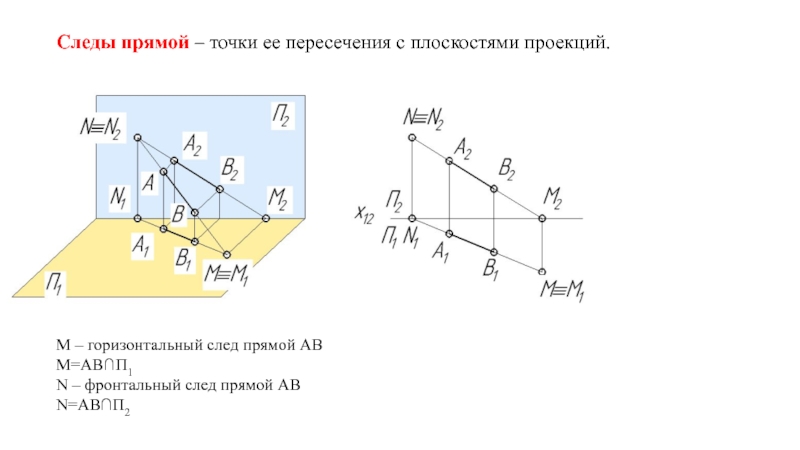
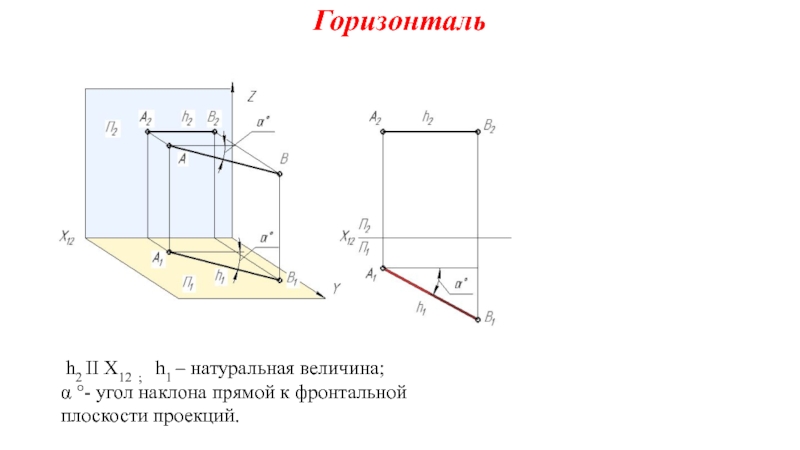
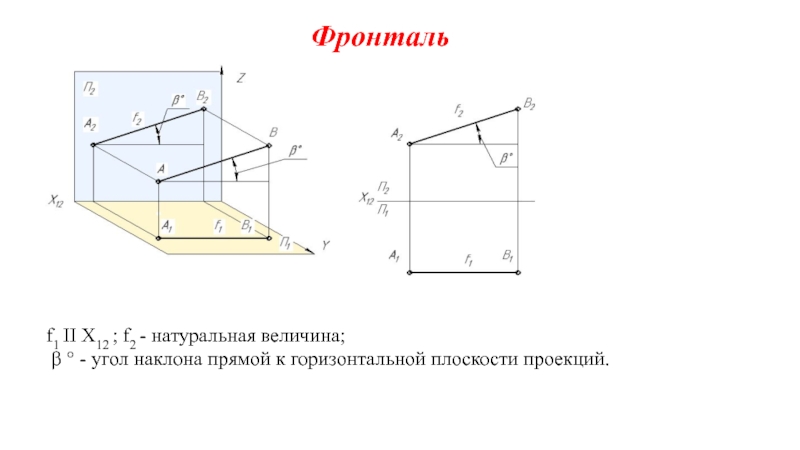
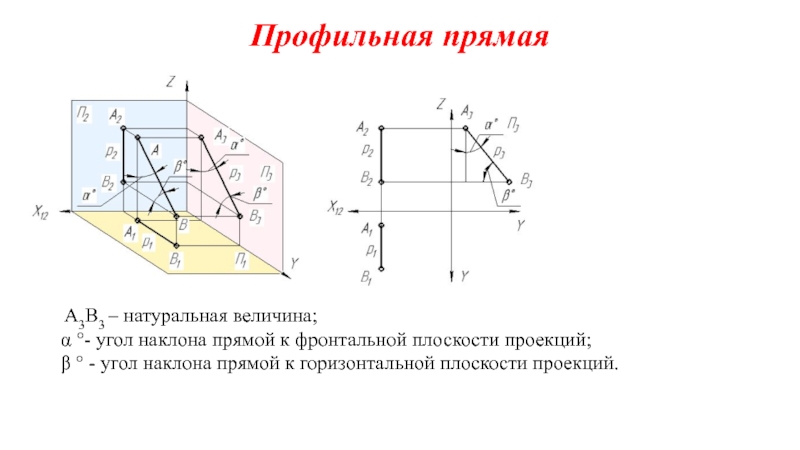
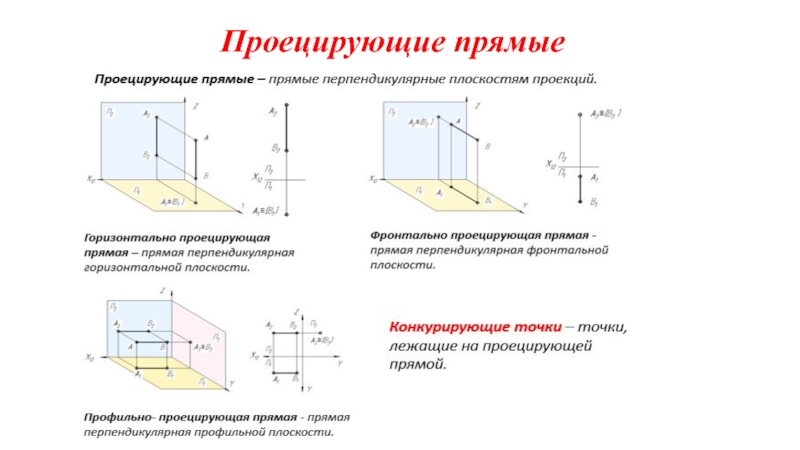
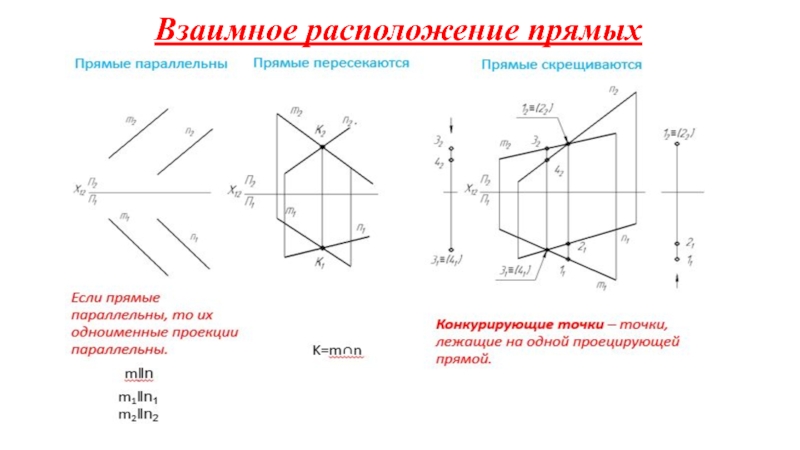
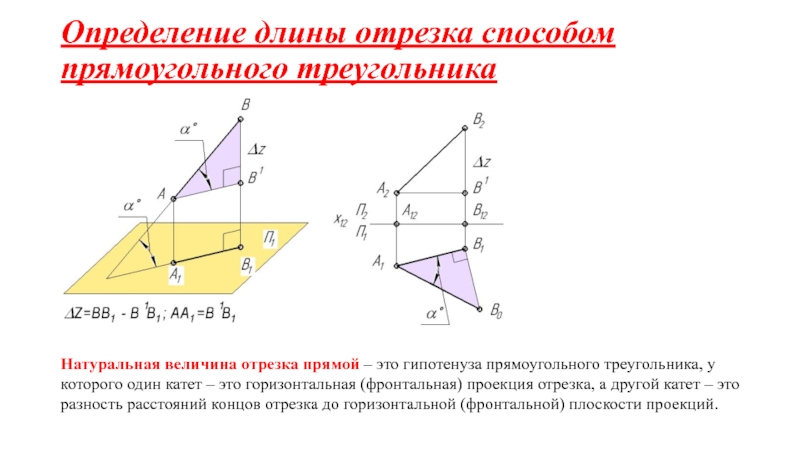
на плоскости.
Предметом начертательной геометрии являются пространственные формы и их

соотношения.

Изображения объектов трехмерного пространства
на плоскости получают методом проецирования.
Поэтому проекционный метод построения
изображений является основным методом НГ.

Проецирование – это получение изображения объекта с помощью проецирующих лучей на плоскость.

лучи (проецирующие прямые), проецируемый объект и плоскость, на которой получается

изображение (плоскость проекций).

В зависимости от положения центра проецирования и
направления проецирующих прямых по отношению
к плоскости проекций, проецирование может быть:
центральным,
параллельным
прямоугольным (ортогональным).

проецирующие прямые
А, В, С – точки пространства
l ⊃S
l ⊂ A,B,C
l

∩П1 = А1, В1, С1

l ⊃S
l ⊂ A,B,C
l ∩П1 = А1, В1, С1

Свойства центрального проецирования
Проекцией точки является точка
Проекцией прямой линии является прямая
Проекцией точки, лежащей на прямой является точка, лежащая на проекции
данной прямой. Если С ⊂ АВ, то C1 ⊂ А1В1.

Точка пересечения линий проецируется в точку пересечения их проекций.

плоскостью проекций
α°- не равно 90°
I, j ⊃ A,

B. A1. B1 = I, j ∩ П1
А1, В1 - параллельные проекции точек

прямых являются параллельные прямые.
Если MN ll DE, то М1

N1llD1E1

5. Отношение отрезков параллельных прямых равно отношению
проекций этих отрезков.
Если MN II DE, то MN/DE = M1N1/D1E1 (MD/DN=M1D1/D1N1)

6. Прямая параллельная плоскости проекций проецируется в
натуральную величину.
Если MN II П1, то MN= M1N1

проекций)

Свойства прямоугольного проецирования

1 – 6 справедливы

косинус угла наклона прямой к плоскости проекций.
0 ˂ А1 В1

˂ АВ
АВ = А1 В1 * cos α

МВ‖А1В1

МВ=А1В1

АМ⊥ВМ
AM=AA1-A1M
АВ – натуральная величина
отрезка

сторон прямого угла параллельна одной из
плоскостей проекций, а другая

ей не перпендикулярна,
то прямой угол на эту плоскость проецируется без искажения.

a⊥b, a‖П1


Если a‖П1, то a1⊥b1

– по проекциям воссоздание пространственной модели
Прямая и обратная задачи
К чертежу

предъявляются следующие требования: обратимость, точность, простота, наглядность.

взаимосвязанных ортогональных проекций.

ось проекций
П2⊥П1
АА2=А1А12 расстояние до фронтальной плоскости
АА1 = А2А12

расстояние до горизонтальной плоскости
А2А1 – линия связи
А2А1 ⊥ Х12
Две проекции точки определяют ее положение в пространстве

Комплексный чертеж точки

общего положения.
Прямая на комплексном чертеже может быть задана:
двумя точками (А,

В);
своими проекциями (m1, m2).

горизонтальный след прямой AB
М=AB∩П1
N – фронтальный след прямой AB
N=AB∩П2

это прямые параллельные и перпендикулярные плоскостям проекций.
Прямые уровня
Прямые уровня –

прямые параллельные плоскостям проекций.

Различают три линии уровня:
1) прямую, параллельную горизонтальной плоскости проекций; называют горизонтальной или горизонталью h; 2) прямую, параллельную фронтальной плоскости проекций; называют фронтальной или фронталью f; 3) прямую, параллельную профильной плоскости проекций; называют профильной р.
Каждая линия уровня будет проецироваться в натуральную величину на ту плоскость проекций, которой она параллельна, углы наклона, которые эта прямая образует с двумя другими плоскостями проекций, также будут проецироваться на эту плоскость без искажения.

α °- угол наклона прямой к фронтальной плоскости проекций.

- угол наклона прямой к горизонтальной плоскости проекций.

наклона прямой к фронтальной плоскости проекций;
β ° - угол

наклона прямой к горизонтальной плоскости проекций.

это гипотенуза прямоугольного треугольника, у которого один катет – это

горизонтальная (фронтальная) проекция отрезка, а другой катет – это разность расстояний концов отрезка до горизонтальной (фронтальной) плоскости проекций.