Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Нестехиометрия в кристалле АВ
Содержание
- 1. Нестехиометрия в кристалле АВ
- 2. Нестехиометрия в кристалле А2В3Разупорядоченность по Шоттки pA>>pBЧастное
- 3. Нестехиометрия в кристалле АВl – сумма стехиометрических
- 4. О показатели степени в уравнении xi=KpizРассмотрим
- 5. О показатели степени в уравнении xi=KpizКонцентрация одного вида дефектов определяется выражениемОбозначивполучаем
- 6. О показатели степени в уравнении xi=KpizВ
- 7. Квазихимический анализ нестехиометрии PbSДопустим, что при растворении
- 8. Квазихимический анализ нестехиометрии PbSДопустим, что при растворении
- 9. Квазихимический анализ нестехиометрии PbSДля перевода давления пара
- 10. Нестехиометрия трехкомпонентных соединенийКаждый из трех компонентов
- 11. Нестехиометрия трехкомпонентных соединенийКаждый из трех компонентов
- 12. ПеровскитCaOTi
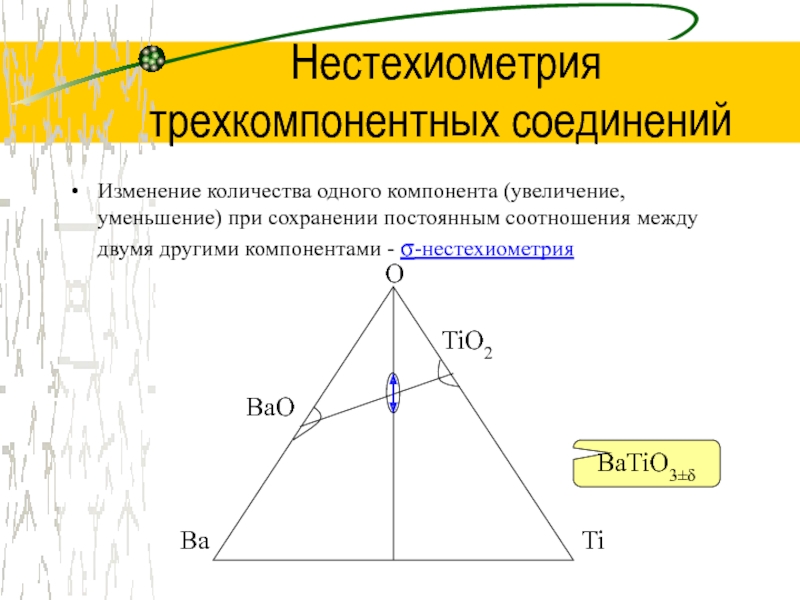
- 13. Нестехиометрия трехкомпонентных соединенийИзменение количества одного компонента
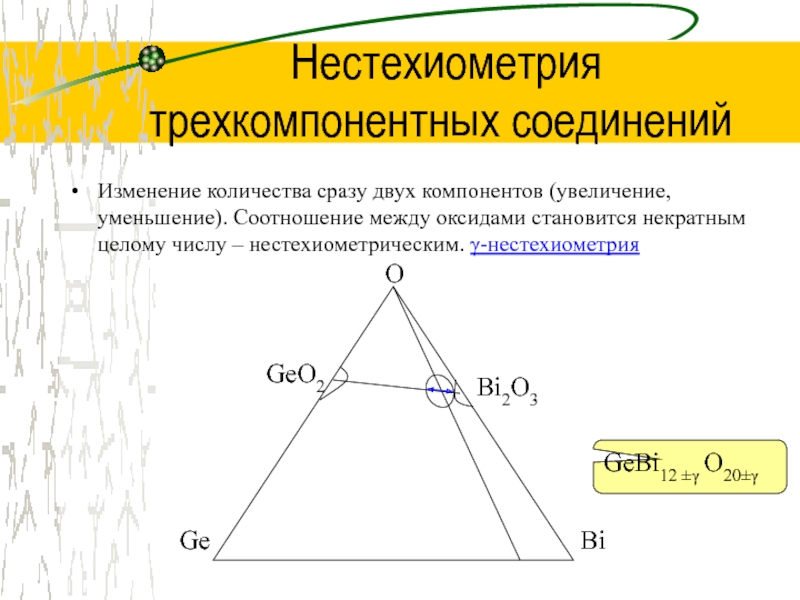
- 14. Нестехиометрия трехкомпонентных соединенийИзменение количества сразу двух
- 15. Нестехиометрия трехкомпонентных соединенийσ -нестехиометрия – образование
- 16. Нестехиометрия соединения ABO3Тепловой беспорядок (термическая диссоциация)
- 17. Нестехиометрия соединения ABO3σ -нестехиометрияγ-нестехиометрия
- 18. Нестехиометрия соединения ABO3Таким образом, в кристалле
- 19. Нестехиометрия β-глинозема Na2O·11Al2O3 (NaAl11O17)Ю.Д.ТретьяковТепловой беспорядок по
- 20. Нестехиометрия β-глинозема Na2O·11Al2O3 (NaAl11O17)Ю.Д.ТретьяковС учетом электронной разупорядоченности видаУравнение электронейтральности имеет вид
- 21. Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3 Ю.Д.ТретьяковТогда условие электронейтральности принимает вид
- 22. Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3 Ю.Д.ТретьяковЧтобы определить концентрацию «дырок» используем реакцию
- 23. Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3 Ю.Д.ТретьяковПосле ряда подстановок
- 24. Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3 Ю.Д.ТретьяковПри увеличении количества
- 25. Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3 Ю.Д.ТретьяковЧтобы определить концентрацию «дырок» используем реакцию С учетом термической диссоциации
- 26. Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3 Ю.Д.Третьяковln αln [ ]
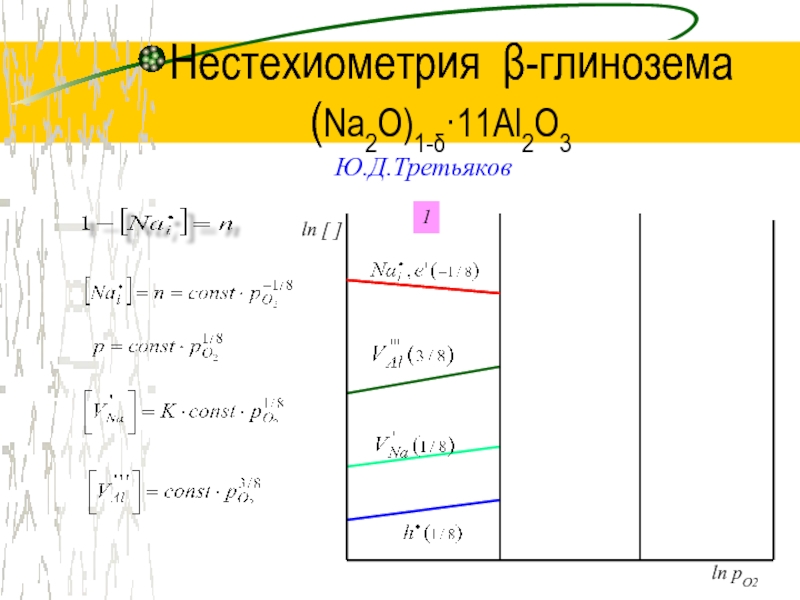
- 27. Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3 Ю.Д.Третьяков1
- 28. Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3 Ю.Д.Третьяковln [ ]2
- 29. Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3 Ю.Д.Третьяковln [ ]3
- 30. Общее уравнение для дефектов нестехиометрииl –
- 31. Скачать презентанцию
Нестехиометрия в кристалле А2В3Разупорядоченность по Шоттки pA>>pBЧастное условие электронейтральности будет иметь видТогда концентрация вакансий B будет определяться выражениемl – сумма стехиометрических коэффициентов исходныхm – сумма стехиометрических
Слайды и текст этой презентации
Слайд 2Нестехиометрия в кристалле А2В3
Разупорядоченность по Шоттки pA>>pB
Частное условие электронейтральности будет
иметь вид
Тогда концентрация вакансий B будет определяться выражением
l – сумма
стехиометрических
коэффициентов исходныхm – сумма стехиометрических коэффициентов продуктов
Слайд 3Нестехиометрия в кристалле АВ
l – сумма стехиометрических
коэффициентов исходных веществ
m – сумма стехиометрических
коэффициентов продуктов реакции
Слайд 4О показатели степени
в уравнении xi=Kpiz
Рассмотрим общий случай образования любых
типов дефектов при растворении А в АВ
Учитывая принципы постоянства отношения
числа разносортных узлов и электронейтральности кристалла, можно говорить об определенной эквивалентности образования различных дефектов
Слайд 5О показатели степени
в уравнении xi=Kpiz
Концентрация одного вида дефектов определяется
выражением
Обозначив
получаем
Слайд 6О показатели степени
в уравнении xi=Kpiz
В случае образования простых (не
ассоциированных) точечных дефектов
l – число частиц, которое внедряется в кристалл
из сосуществующей фазы (пар, расплав)m – суммарное число частиц (или квазичастиц) различного вида, которые образовались в кристалле в результате внедрения l частиц из сосуществующей фазы
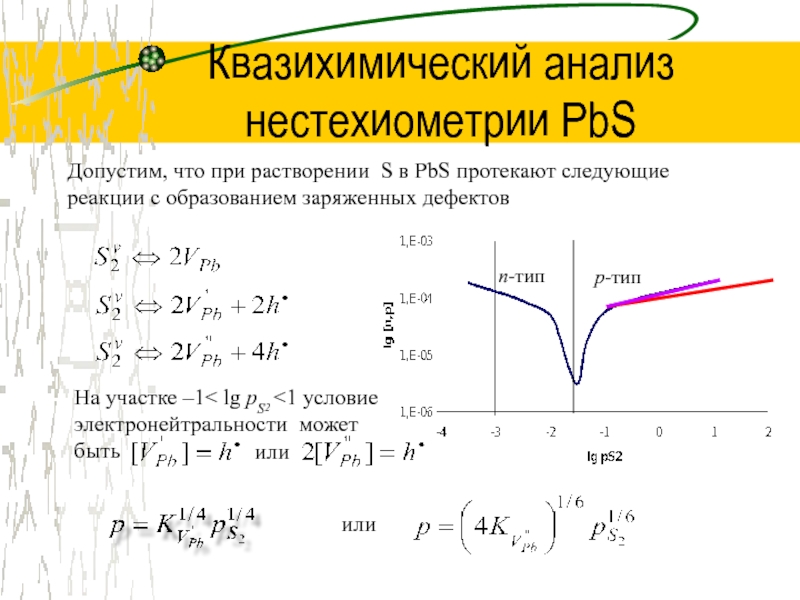
Слайд 7Квазихимический анализ нестехиометрии PbS
Допустим, что при растворении S в PbS
протекают следующие реакции с образованием заряженных дефектов
На участке –1< lg
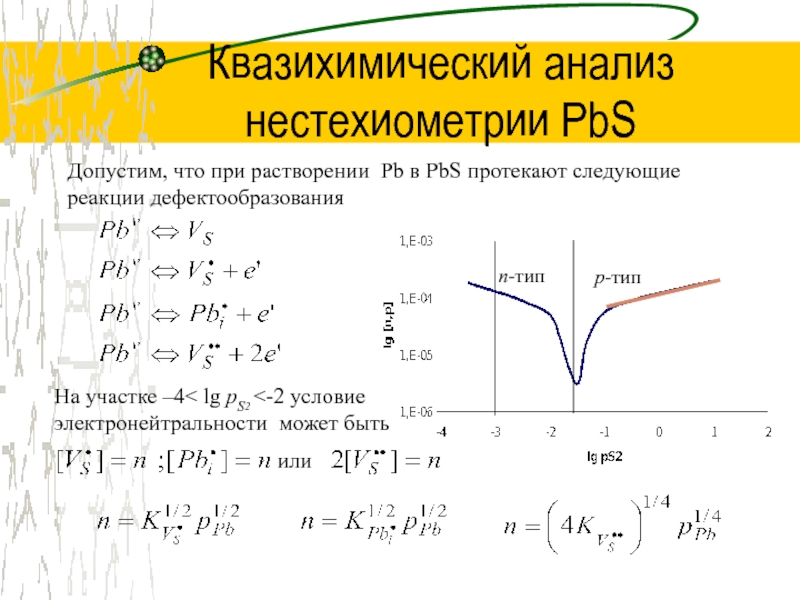
pS2 <1 условие электронейтральности может быть
Слайд 8Квазихимический анализ нестехиометрии PbS
Допустим, что при растворении Pb в PbS
протекают следующие реакции дефектообразования
На участке –4< lg pS2
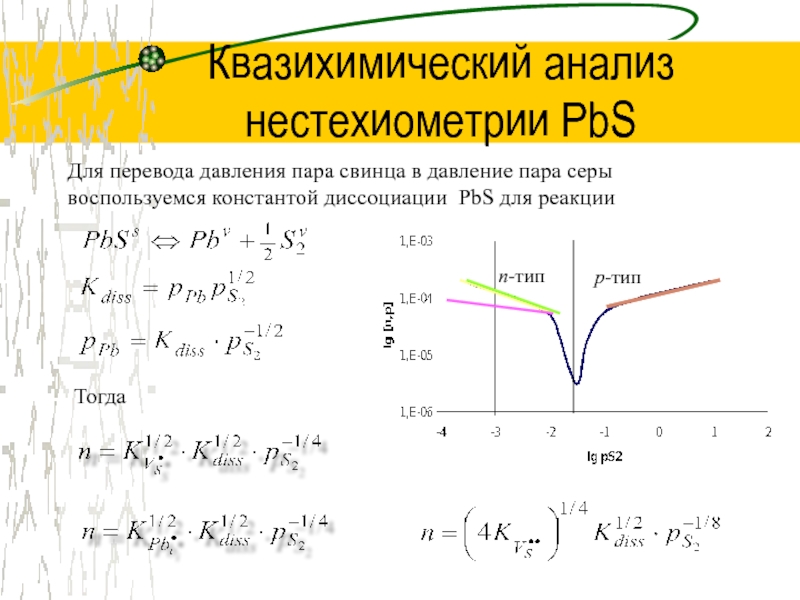
электронейтральности может быть
Слайд 9Квазихимический анализ нестехиометрии PbS
Для перевода давления пара свинца в давление
пара серы воспользуемся константой диссоциации PbS для реакции
Тогда
Слайд 10 Нестехиометрия трехкомпонентных соединений
Каждый из трех компонентов образует свою собственную
подрешетку
Кристаллы с двумя подрешетками – катионной и анионной; третий компонент
равномерно распределен в узлах катионной или анионной подрешеток
Слайд 11 Нестехиометрия трехкомпонентных соединений
Каждый из трех компонентов образует свою собственную
подрешетку
Перовскиты – A2B4O3 (CaTiO3, BaTiO3, PbTiO3, PbZrO3)
Силлениты – MeO2·6Bi2O3 (MeBi12O20)
Шпинели
- MeO·Fe2O3 (MeBi2O4)Полиалюминаты натрия – Na2O·11Al2O3 (NaAl11O17)
Слайд 13 Нестехиометрия трехкомпонентных соединений
Изменение количества одного компонента (увеличение, уменьшение) при
сохранении постоянным соотношения между двумя другими компонентами - σ-нестехиометрия
BaO
TiO2
BaTiO3±δ
Слайд 14 Нестехиометрия трехкомпонентных соединений
Изменение количества сразу двух компонентов (увеличение, уменьшение).
Соотношение между оксидами становится некратным целому числу – нестехиометрическим. γ-нестехиометрия
GeO2
Bi2O3
GeBi12
±γ O20±γ
Слайд 15 Нестехиометрия трехкомпонентных соединений
σ -нестехиометрия – образование обычных точечных дефектов
PbTiO3=1/2σO2+PbTiO3-
σ
γ-нестехиометрия - при больших значениях γ может приводить к кристаллографическим
сдвигам и образованию протяженных дефектов
PbTiO3= γ PbO+Pb1- γ TiO3- γ 
Слайд 18 Нестехиометрия соединения ABO3
Таким образом, в кристалле образуются следующие дефекты
Для
данного набора дефектов уравнение электронейтральности имеет вид
При образовании дефектов
с другими эффективными зарядами уравнение электронейтральности принимает вид 
Слайд 19 Нестехиометрия β-глинозема Na2O·11Al2O3 (NaAl11O17)
Ю.Д.Третьяков
Тепловой беспорядок по Френкелю
Растворение кислорода приводит
к образованию дефектов Шоттки
Растворение Na2O сопровождается внедрением избыточного Na в
междоузлия
Слайд 20 Нестехиометрия β-глинозема Na2O·11Al2O3 (NaAl11O17)
Ю.Д.Третьяков
С учетом электронной разупорядоченности вида
Уравнение электронейтральности
имеет вид
Слайд 21 Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3
Ю.Д.Третьяков
Тогда условие электронейтральности принимает вид
Слайд 22 Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3
Ю.Д.Третьяков
Чтобы определить концентрацию «дырок» используем реакцию
Слайд 23 Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3
Ю.Д.Третьяков
После ряда подстановок получим
Так как
процесс протекает при PO2=const, то
С учетом соотношения об электронном
разупорядочении
Слайд 24 Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3
Ю.Д.Третьяков
При увеличении количества растворенного Na2O тепловое
разупорядочение перестает быть доминирующим и дефектообразование начинает контролироваться реакцией
Слайд 25 Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3
Ю.Д.Третьяков
Чтобы определить концентрацию «дырок» используем реакцию
С учетом термической диссоциации
![Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3 Ю.Д.Третьяковln αln [ ]](/img/tmb/2/147250/63d915a3176d77704c5e329d48cc4b95-800x.jpg "Нестехиометрия в кристалле АВ Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3 Ю.Д.Третьяковln αln [ ]")
![Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3 Ю.Д.Третьяковln [ ]2](/img/tmb/2/147250/0f91db6f029b45b5578c882b3c976582-800x.jpg "Нестехиометрия в кристалле АВ Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3 Ю.Д.Третьяковln [ ]2")
![Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3 Ю.Д.Третьяковln [ ]3](/img/tmb/2/147250/c3eaf06d3655e72f20f428eb2b7d6bd5-800x.jpg "Нестехиометрия в кристалле АВ Нестехиометрия β-глинозема (Na2O)1-δ·11Al2O3 Ю.Д.Третьяковln [ ]3")
Слайд 30Общее уравнение для
дефектов нестехиометрии
l – сумма стехиометрических коэффициентов исходных
веществ
m – сумма стехиометрических коэффициентов продуктов реакции
При T=const
