Слайд 1ОСНОВЫ ФИНАНСОВОЙ МАТЕМАТИКИ
Мостовщикова ирина Александровна, ст. преп. Каф. «Финансовые технологии»
Слайд 2ПРЕДМЕТ и задачи дисциплины
Предмет дисциплины:
количественный анализ условий (параметров) и
результатов финансово-кредитных операций, инвестиционных проектов, коммерческих сделок
Задачи дисциплины:
Измерение конечных финансовых
результатов операции (сделки, контракта) для каждой из участвующих сторон
Учет ценных бумаг
Установление взаимосвязи между отдельными параметрами сделки и определение параметров сделки, исходя из заданных условий
Анализ последствий изменения условий операции
Разработка планов выполнения финансовых операций
Определение эквивалентности параметров сделки для получения равной отдачи от затрат, произведенных различными способами
Слайд 3Понятие финансовой операции
Любая финансовая операция (сделка) подразумевает наличие следующих параметров:
стоимостные характеристики (стоимость начальная и конечная, стоимость покупки и продажи,
размер повторяющегося платежа и т.д.)
временные параметры (срок операции, периодичность выплат, частота капитализаций)
процентные ставки (процентная и учетная)
Слайд 4Концепция временной стоимости денег
! Ценность денег с течением времени меняется,
в связи с чем, равные по абсолютной величине суммы денег,
относящиеся к разным моментам времени, не равноценны
Концепция временной стоимости денег может рассматриваться в 2-х аспектах:
Обесценивание денежной наличности с течением времени (инфляция)
Обращение капитала, т.е. деньги вложенные в дело приносят доход
Слайд 5Концепция временной стоимости денег
В силу того, что денежные суммы находятся
в разных периодах времени, они будут иметь разную ценность (стоимость),
поэтому их нельзя суммировать и сравнивать при принятии финансовых решений!
Их сравнение допустимо только при «приведении» таких сумм к одному моменту времени.
Поэтому ключевым понятием финансовой математики является понятие приведенной стоимости.
В любой операции мы имеем дело с двумя типами стоимости (начальной PV и конечной FV)
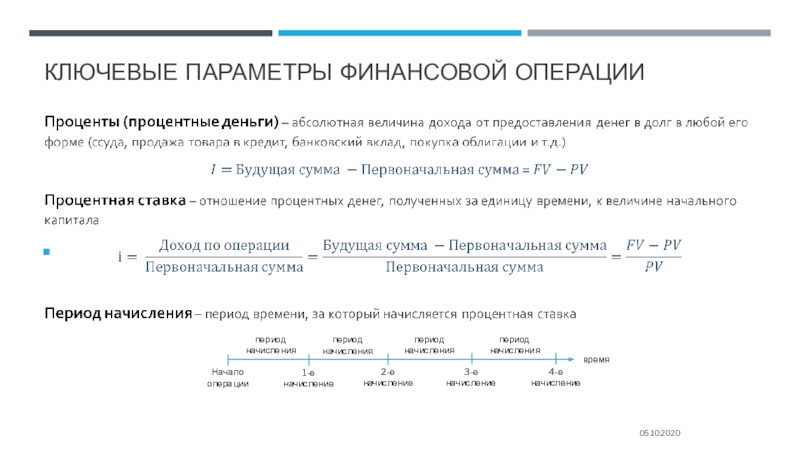
Слайд 6ключевые параметры финансовой операции
Начало
операции
1-е
начисление
2-е
начисление
3-е
начисление
4-е
начисление
время
период
начисления
период
начисления
период
начисления
период
начисления
Слайд 7Процентная ставка
На размер процентной ставки влияют следующие факторы:
общее состояние
экономики;
вид сделки;
валюта сделки;
срок сделки;
особенности кредитора и
заемщика;
история предыдущих отношений между кредитором и заемщиком.
Схемы начисления процентов:
схема простых процентов (предполагает неизменность базы начисления);
схема сложных процентов (начисленные проценты присоединяются к первоначальной базе на каждом этапе начисления).
2 принципа ведения расчетов:
от настоящего к будущему (применяется ставка наращения);
от будущего к настоящему (применяется дисконтная ставка (учетная)).
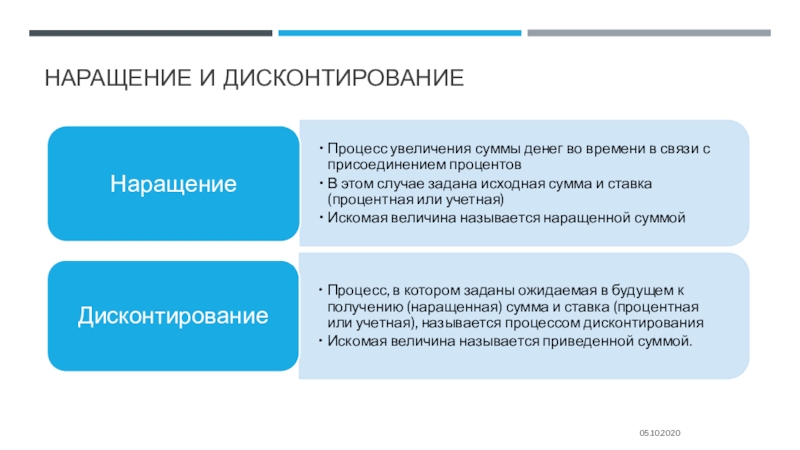
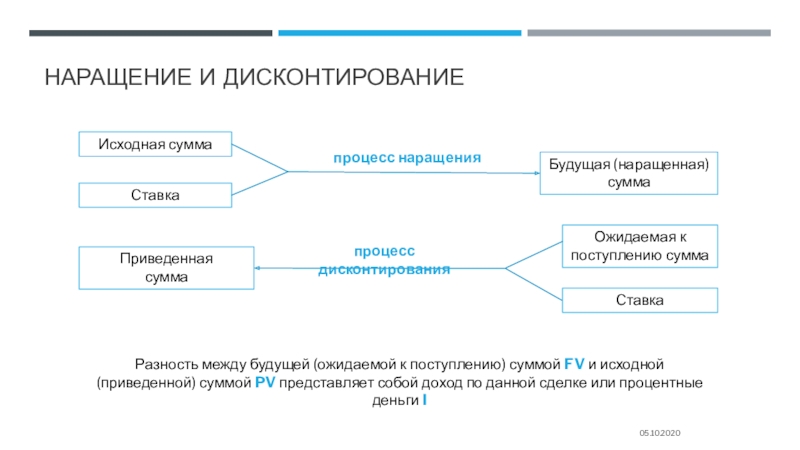
Слайд 9Наращение и дисконтирование
Исходная сумма
Cтавка
Будущая (наращенная) сумма
процесс наращения
Ожидаемая к поступлению
сумма
Cтавка
Приведенная
сумма
процесс дисконтирования
Разность между будущей (ожидаемой к поступлению) суммой FV
и исходной (приведенной) суммой PV представляет собой доход по данной сделке или процентные деньги I
Слайд 10принятые обозначения
I – процентные деньги (абсолютный доход по операции);
FV –
будущая стоимость вложенной суммы;
PV – настоящая стоимость имеющейся суммы;
i –
годовая процентная ставка;
d – годовая учетная ставка;
n – срок ссуды (в годах).
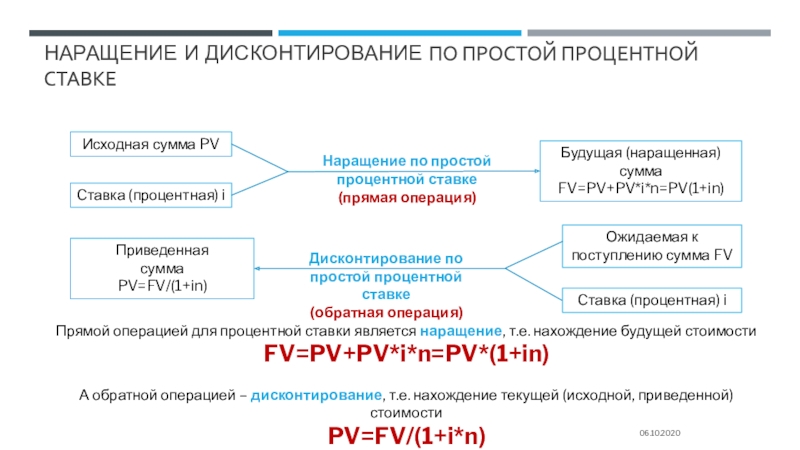
Слайд 12Наращение и дисконтирование ПО ПРОСТОЙ ПРОЦЕНТНОЙ СТАВКЕ
Исходная сумма
PV
Cтавка (процентная) i
Будущая (наращенная) сумма
FV=PV+PV*i*n=PV(1+in)
Наращение по простой процентной ставке
(прямая
операция)
Ожидаемая к поступлению сумма FV
Cтавка (процентная) i
Приведенная
сумма
PV=FV/(1+in)
Дисконтирование по простой процентной ставке
(обратная операция)
Прямой операцией для процентной ставки является наращение, т.е. нахождение будущей стоимости
FV=PV+PV*i*n=PV*(1+in)
А обратной операцией – дисконтирование, т.е. нахождение текущей (исходной, приведенной) стоимости
PV=FV/(1+i*n)
Слайд 13Решим пример
1. Вы положили на счет 100 000 рублей под
8% годовых. Ставка простая. Какой суммой Вы будете располагать через
3 года?
Дано:
PV =100 000 руб., i=0,08, n=3 года, FV=?
Решение:
FV=PV(1+in)=100 000*(1+0,08*3)=124 000 рублей.
2. Вы планируете поехать в отпуск через 2 года. Ориентировочная стоимость путевки составит 250 000 рублей. Какую сумму нужно положить на счет сегодня, чтобы с учетом начисления 10% годовых Вы накопили нужную сумму к указанному сроку? Проценты простые.
Дано:
FV =250 000 руб., i=0,1, n=2 года, PV=?
Решение:
PV=FV/(1+in)=250 000 / (1+0,1*2)=208334 рубля.
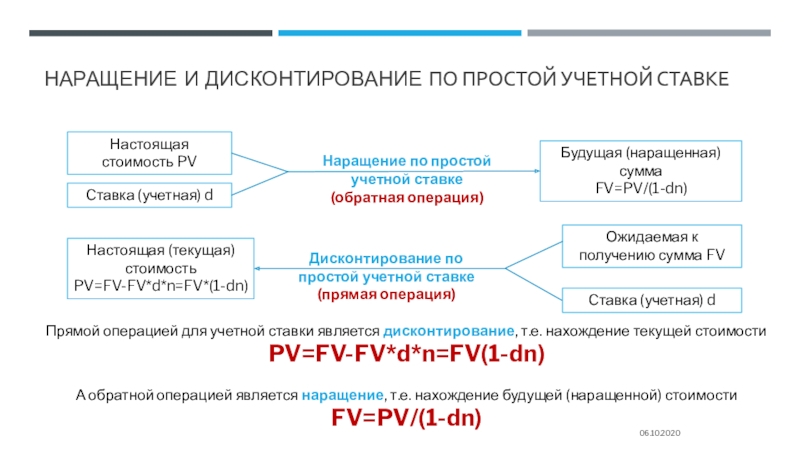
Слайд 14Наращение и дисконтирование ПО ПРОСТОЙ учетной СТАВКЕ
Настоящая стоимость
PV
Cтавка (учетная) d
Будущая (наращенная) сумма
FV=PV/(1-dn)
Наращение по простой учетной ставке
(обратная
операция)
Ожидаемая к получению сумма FV
Cтавка (учетная) d
Настоящая (текущая)
стоимость
PV=FV-FV*d*n=FV*(1-dn)
Дисконтирование по простой учетной ставке
(прямая операция)
Прямой операцией для учетной ставки является дисконтирование, т.е. нахождение текущей стоимости
PV=FV-FV*d*n=FV(1-dn)
А обратной операцией является наращение, т.е. нахождение будущей (наращенной) стоимости
FV=PV/(1-dn)
Слайд 15Решим пример
1. Ваш покупатель вместо платы за товар в размере
100 000 рублей предложил Вам вексель номинальной стоимостью 105000 рублей,
возврат долга по которому ожидается через полгода. Согласитесь ли Вы на данное предложение, если банк может учесть такой вексель по ставке 7% годовых?
Дано:
FV =105 000 руб., d=0,07, n=0,5 года, PV=?
Решение:
PV = FV(1-dn) = 105 000*(1-0,07*0,5) = 101 325 рублей. Взять вексель выгоднее, т.к. по нему Вы сможете получить больше.
2. Вексель какого номинала нужно выдать, чтобы при сроке погашения векселя в 1 год и действующей учетной ставке 6%, клиент смог сегодня учесть его в банке за 150000 рублей?
Дано:
PV=150 000 руб., d=0,06, n=1 год, FV=?
Решение:
FV = PV/(1-dn) = 150 000 / (1-0,06*1) = 159 575 рублей.
Слайд 16Аспекты применения формул Простых процентов
Слайд 18Точность начисления процентов
При расчете процентов применяются 2 временные базы:
Т
= 360 – обыкновенные или коммерческие проценты;
Т = 365,
366 – точные проценты.
Число дней ссуды t также можно измерить:
приближенно (любой месяц в году принимается равным 30 дням);
точно (точный подсчет числа дней между датой выдачи и датой погашения ссуды согласно календарю).
!!! Принято день выдачи и день погашения ссуды считать за 1 полный день !!!
Слайд 21Изменение процентной ставки во времени
В кредитных соглашениях иногда предусматриваются изменяющиеся
во времени процентные ставки. Если это простые ставки, то наращенная
на конец срока сумма определяется следующим образом:
Проценты будут начисляться всегда на первоначальную стоимость, таким образом в конце срока мы будем иметь PV, а также сумму процентов от PV по разным ставкам.
Слайд 23Реинвестирование по простым процентам
Слайд 24Изменение депозитных сумм
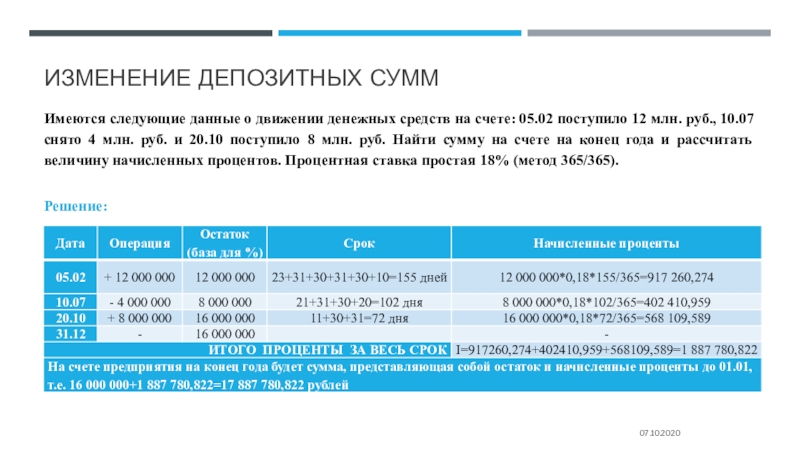
Имеются следующие данные о движении денежных средств на
счете: 05.02 поступило 12 млн. руб., 10.07 снято 4 млн.
руб. и 20.10 поступило 8 млн. руб. Найти сумму на счете на конец года и рассчитать величину начисленных процентов. Процентная ставка простая 18% (метод 365/365).
Решение:
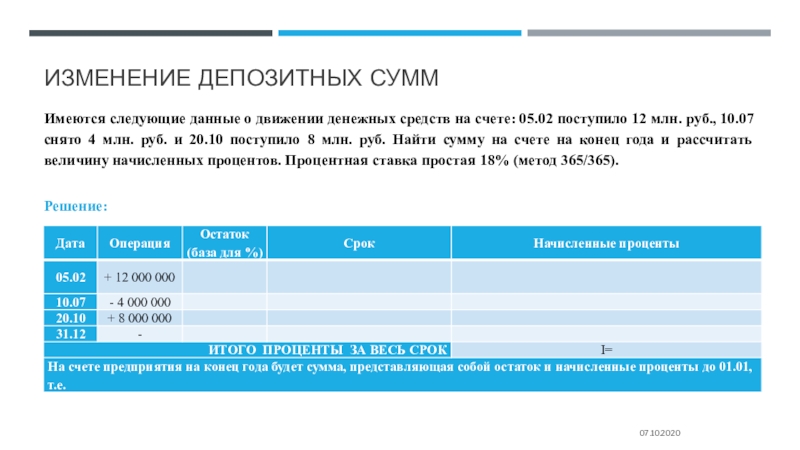
Слайд 25Изменение депозитных сумм
Имеются следующие данные о движении денежных средств на
счете: 05.02 поступило 12 млн. руб., 10.07 снято 4 млн.
руб. и 20.10 поступило 8 млн. руб. Найти сумму на счете на конец года и рассчитать величину начисленных процентов. Процентная ставка простая 18% (метод 365/365).
Решение:
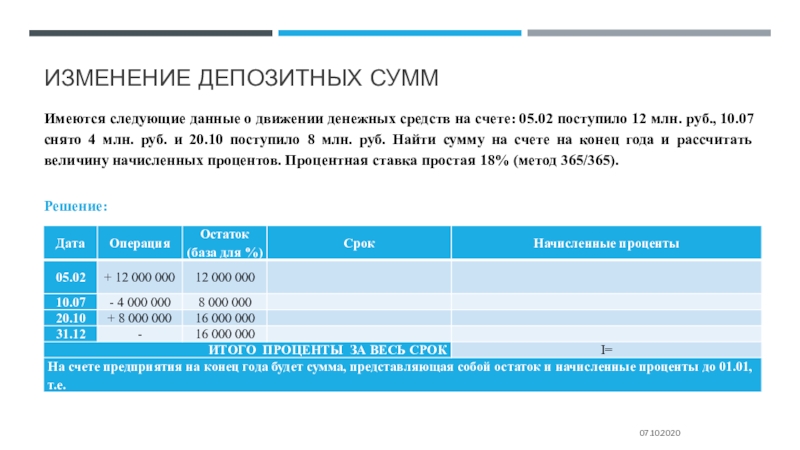
Слайд 26Изменение депозитных сумм
Имеются следующие данные о движении денежных средств на
счете: 05.02 поступило 12 млн. руб., 10.07 снято 4 млн.
руб. и 20.10 поступило 8 млн. руб. Найти сумму на счете на конец года и рассчитать величину начисленных процентов. Процентная ставка простая 18% (метод 365/365).
Решение:
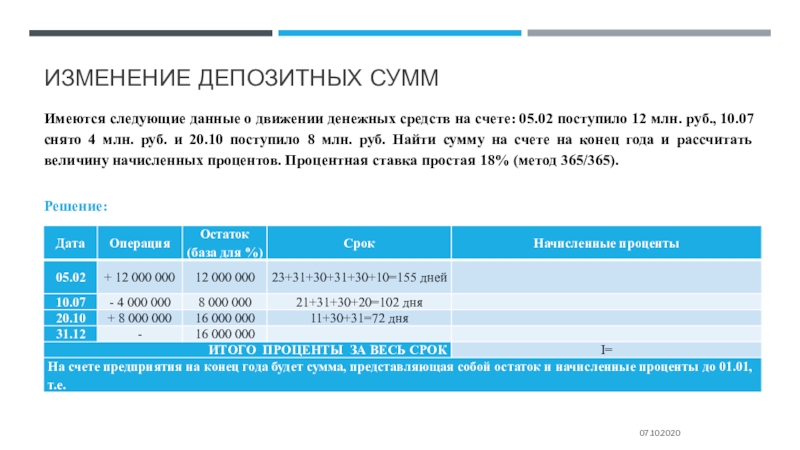
Слайд 27Изменение депозитных сумм
Имеются следующие данные о движении денежных средств на
счете: 05.02 поступило 12 млн. руб., 10.07 снято 4 млн.
руб. и 20.10 поступило 8 млн. руб. Найти сумму на счете на конец года и рассчитать величину начисленных процентов. Процентная ставка простая 18% (метод 365/365).
Решение:
Слайд 29Сложные проценты
Отличие сложных процентов от простых заключается в том, что
начисляться они будут уже не на первоначальную стоимость (как в
случае с простыми процентами), а на первоначальную сумму с процентами прошлого периода. Поэтому сложные проценты часто называют «проценты на проценты».
– коэффициент (множитель) наращения по сложным процентам – показывает, во сколько раз увеличилась первоначальная сумма денег при заданных значениях i и n.
Обычно используется метод 365/365.
Слайд 30ОСНОВНЫЕ ФОРМУЛЫ Сложных процентов
Слайд 31Решим пример
1. В день рождения внука бабушка положила в банк
1000 долларов под 8% годовых. Какой будет эта сумма к
восемнадцатилетию внука при условии начисления сложных процентов?
Решение:
Это классический пример задачи на наращение.
FV = PV(1+i)n = 1000(1+0,08)18 = 3996 долларов
2. Рассчитайте, какую сумму нужно депонировать в банк, чтобы по истечении трех лет получить 60 000 рублей, если сложная процентная ставка составляет 15% годовых.
Решение:
Это пример задачи на дисконтирование.
PV=FV/(1+i)n = 60 000/(1+0,15)3 = 39 451 рубль
Слайд 32Аспекты применения формул сложных процентов
Слайд 33Изменение сложной процентной ставки
В случае изменения процентных ставок в течение
одной операции общий множитель наращения определяется, как произведение частных.
Поэтому
формула наращения по изменяющейся сложной процентной ставке будет иметь вид:
FV = PV(1+i1)n1 (1+i2)n2 … (1+ik)nk,
где i1, i2 … ik – последовательные значения ставок;
n1, n2 … nk – периоды, в течение которых действуют соответствующие ставки.
Слайд 35Начисление процентов за дробное число лет
Часто срок в годах для
начисления процентов не является целым числом. В этом случае используют
2 метода:
расчет ведется непосредственно по формуле: FVn = PV(1+i)n (общий порядок расчета);
проценты за целое число лет начисляются по схеме сложных процентов, а за дробную часть срока - по формуле простых процентов (смешанный метод): FVn = PV(1+i)a (1+ib),
где n = a + b – срок ссуды, а – целое число лет, b – дробная часть года.
ПРИМЕР: Кредит в размере 3 млн. руб. выдан на 3 года и 160 дней (n = 3 и 160/365 = 3,43836 года) под 16,5% сложных годовых. Рассчитать сумму долга на конец срока.
FV = 3 000 000 (1+0,165)3,43836 = 5 071 935,98 руб.
FV = 3 000 000 (1+0,165)3 (1+0,165*0,43836) = 5 086 592,10 руб.
Слайд 36Сравнение роста по простым и сложным процентам
Обозначим is
ставку простых процентов, i – ставку сложных процентов, тогда:
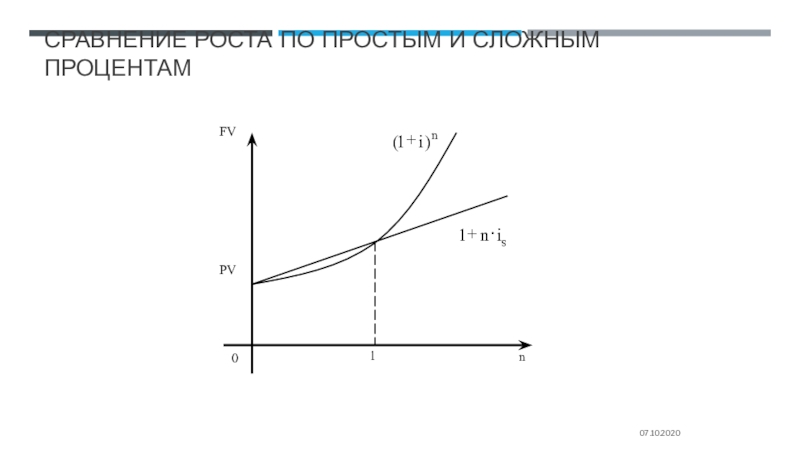
Для срока
меньше года простые проценты больше сложных:
Для срока больше года сложные проценты больше простых:
Для срока, равного году, множители наращения равны друг другу:
Слайд 37Сравнение роста по простым и сложным процентам
s
Слайд 38Сравнение роста по простым и сложным процентам
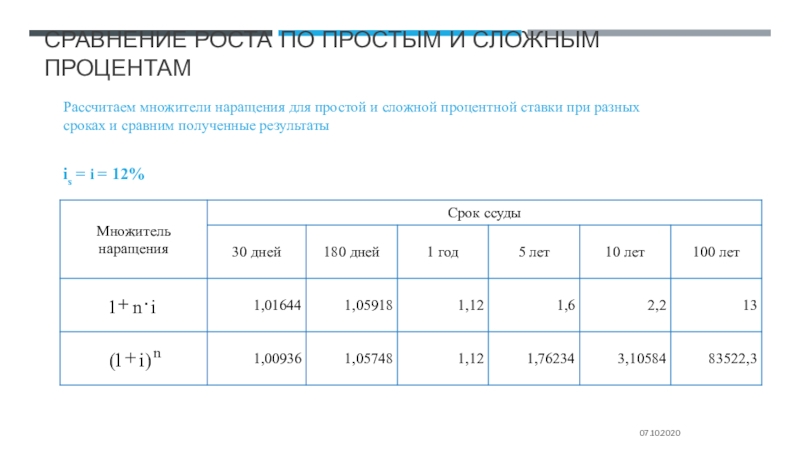
is = i =
12%
Рассчитаем множители наращения для простой и сложной процентной ставки при
разных сроках и сравним полученные результаты
Слайд 39Внутригодовое начисление процентов
Обозначим годовую ставку – j.
Если число периодов
начисления в году – m,
то ставка за конкретный период
начисления будет j/m,
и формула наращения будет следующей:
Т.к. n – срок финансовой операции в годах, то m∙n – общее кол-во периодов начисления.
Ставку j называют номинальной (nominal rate).
Слайд 40Решим пример
Какой величины достигнет долг, равный 1 млн руб., через
3 года при росте по сложной ставке 15,5% годовых. Проценты
начисляются ежеквартально?
Решение:
FV=
!!! Чем чаще начисляются проценты, тем быстрее идет процесс наращения.
Т.е. при использовании одинаковой процентной ставки сумма наращения будет тем больше, чем чаще происходит капитализация. Например, при ставке j = 12%, наращенная за год стоимость 1 д.е. в зависимости от частоты начисления будет меняться следующим образом:
Слайд 41Эффективная ставка
Используемая в расчетах годовая базовая ставка j называется номинальной.
Эффективная
ставка процента измеряет тот реальный относительный доход, который получается в
целом за год. Т.е., эффективная ставка – это такая годовая ставка сложных процентов (iэф), которая дает тот же результат, что и m-разовое начисление процентов по ставке j/m.
Чтобы использование двух ставок (эффективной и номинальной) давало одинаковый результат, множители наращения должны быть равны:
(1 + i)n = (1 + j/m)mn => iэф = (1 + j/m)m – 1
При m > 1 эффективная ставка больше номинальной.
Слайд 42Решим пример
Номинальная ставка – 22% годовых. Проценты начисляются и присоединяются
к основной сумме долга 4 раза в год. Определите эффективную
ставку процента.
Решение:
iэф = (1 + j/m)m – 1
iэф = (1+0,22/4)4– 1 = 0,2388
Получается, что при ежеквартальной капитализации процентов, начисляемых по ставке 22% годовых сумма реально увеличится не на 22%, а на 23,88%!
Слайд 43Дисконтирование по сложной процентной ставке
Дисконтирование по сложной процентной ставке является
процессом, обратным наращению по сложной процентной ставке.
FV = PV(1+ i)n
=> PV = FV / (1 + i)n = FV * 1/(1 + i)n
1/(1 + i)n – дисконтирующий множитель.
Для случаев, когда проценты начисляются m раз в году, получим:
PV = FV / (1 + j/m)mn = FV * 1/(1 + j/m)mn
Величина PV является современной, текущей стоимостью величины FV и может быть рассчитана на любой момент времени до выплаты суммы FV.
Слайд 45учет по сложной учетной ставке
Если в учетных операциях применяют сложную
учетную ставку, то процесс дисконтирования происходит с замедлением, т.к. каждый
раз учетная ставка применяется не к первоначальной сумме (как при простой учетной ставке), а к сумме, дисконтированной на предыдущем шаге во времени.
PV = FV(1 - d)n
ПРИМЕР: Долговое обязательство на сумму 5 млн. руб., срок оплаты которого наступает через 5 лет, продано с дисконтом по сложной учетной ставке 15% годовых. Каков размер полученной за долг суммы и величина дисконта (в тыс. руб.)?
PV = FV(1 - d)n = 5 000*(1 – 0,15)5 = 2 218,5 тыс. руб.
D = 5 000-2 218,5 = 2 781,5 тыс. руб.
Если применить простую учетную ставку того же размера, то
PV = FV(1-d*n) = 5 000*(1 – 5*0,15) = 1 250 тыс. руб.
D = 5 000 – 1 250 = 3 750 тыс. руб.
PV представляет собой текущую сумму долга. Очевидно, что для должника выгоднее использование простой дисконтной ставки.