Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Потоки произвольного вида
Содержание
- 1. Потоки произвольного вида
- 2. Потоки ПальмаПоток событий называется потоком Пальма (потоком
- 3. ПримерНекоторый элемент прибора работает непрерывно до выхода
- 4. Важными образцами потоков Пальма являются потоки Эрланга, которые образуются путем просеивания простейших потоков
- 5. Потоки ЭрлангаПотоком Эрланга k-го порядка Эk называется
- 6. Закон распределения интервала Т между соседними событиями
- 7. Вероятность того, что
- 8. 2) k-ая точка должна попасть на (t,
- 9. Характеристики закона Эрланга k-го порядка
- 10. Обозначим интенсивность потока Эрланга k-го порядка (среднее
- 11. Пусть Λk= Λ=constизменим порядок k закона Эрлангаmt=1/ΛПри
- 12. При помощи потоков Эрланга можно сводить немарковские потоки к марковским
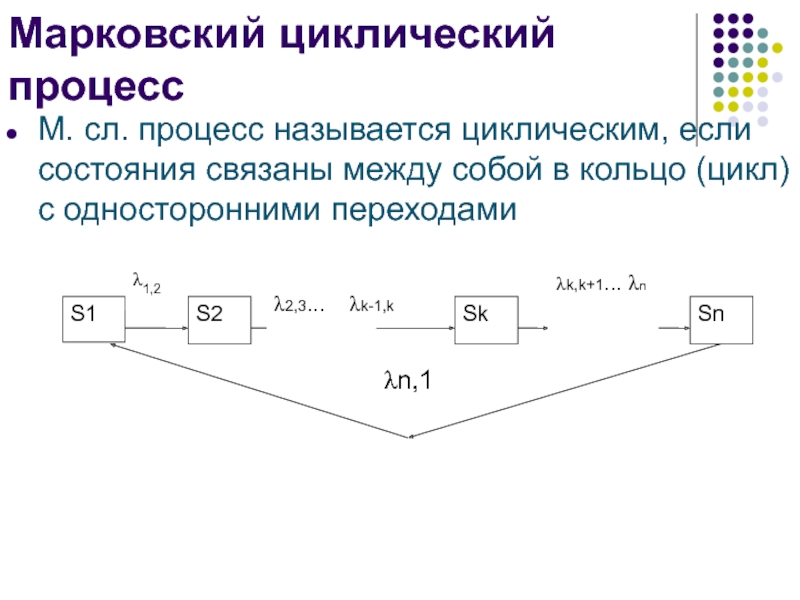
- 13. Марковский циклический процессМ. сл. процесс называется циклическим,
- 14. ПримерЭВМ может находиться в одном из следующих
- 15. Слайд 15
- 16. Ветвящийся циклический процессS1 – исправна, работаетS2 –
- 17. Исходные данныеСр. время исправной работы `t1Ср. время
- 18. Скачать презентанцию
Потоки ПальмаПоток событий называется потоком Пальма (потоком с ограниченным последействием), если промежутки времени между последовательными событиями Т1, Т2, …, Ti,… представляют собой независимые одинаково распределенные случайные величины
Слайды и текст этой презентации
Слайд 2Потоки Пальма
Поток событий называется потоком Пальма (потоком с ограниченным последействием),
Слайд 3Пример
Некоторый элемент прибора работает непрерывно до выхода из строя (отказа),
после чего он мгновенно заменяется новым.
Срок работы элемента случаен.
Если отдельные элементы прибора отказывают независимо друг от друга, то поток отказов (или поток восстановлений, т.к. отказ и восстановление происходят в один и тот же момент) представляет собой поток Пальма
Слайд 4Важными образцами потоков Пальма являются потоки Эрланга, которые образуются путем
просеивания простейших потоков
Слайд 5Потоки Эрланга
Потоком Эрланга k-го порядка Эk называется поток, получающийся из
простейшего, если в нем сохранить каждую k-ю точку, а остальные
выбросить.Простейший поток представляет собой частный случай потока Эрланга (первого порядка – Э1).
Интервал времени между соседними событиями в исходном простейшем потоке распределен по показательному закону
f1(t)=λexp(-λt)
Слайд 6Закон распределения интервала Т между соседними событиями в потоке Эk
называется
законом Эрланга
k-го порядка c плотностью fk(t)
Слайд 7Вероятность того, что
окажется в пределах (t, t+dt):
на участок длиной t должно
попасть ровно (k-1) точек простейшего потока, вероятность этого
Слайд 9Характеристики закона Эрланга k-го порядка
, где каждая из Т распределена по показательному закону
с мат. ожиданием 1/λ и дисперсией , отсюда
Слайд 10Обозначим интенсивность потока Эрланга
k-го порядка (среднее число событий в
единицу времени) Λk,
тогда Λk= λ /k,
а λ=k*Λk
Слайд 11Пусть Λk= Λ=const
изменим порядок k закона Эрланга
mt=1/Λ
При
дисперсия
стремится к 0:Поток Эрланга заданной интенсивности Λ неограниченно приближается к регулярному потоку с постоянным интервалом между событиями Т=1/Λ
Это свойство потоков Эрланга позволяет, задаваясь различными k, получать потоки, обладающие различным последействием – от полного отсутствия последействия (k=1) до жесткой функциональной связи
Слайд 13Марковский циклический процесс
М. сл. процесс называется циклическим, если состояния связаны
между собой в кольцо (цикл) с односторонними переходами
Слайд 14Пример
ЭВМ может находиться в одном из следующих состояний
S1 – исправна,
работает
S2 – остановлена, ведется поиск неисправности
S3 – ведется ремонт
S4 –
ремонт закончен, подготовка к пускуСр. время безотказной работы 0,5 суток
Поиск неисправности в среднем 0,5 ч
Ремонт в среднем 6 ч
Подготовка к пуску в среднем 1 ч
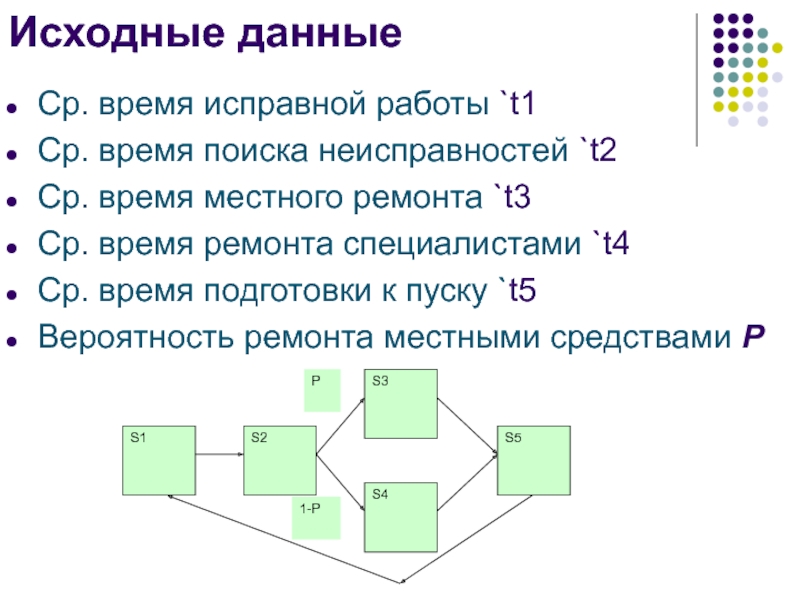
Слайд 16Ветвящийся циклический процесс
S1 – исправна, работает
S2 – остановлена, ведется поиск
неисправности
S3 – неисправность незначительная, ремонт местными средствами
S4 – неисправность значительная,
ремонт бригадой специалистов, S5 - подготовка к пуску
Слайд 17Исходные данные
Ср. время исправной работы `t1
Ср. время поиска неисправностей `t2
Ср.
время местного ремонта `t3
Ср. время ремонта специалистами `t4
Ср. время подготовки
к пуску `t5Вероятность ремонта местными средствами Р