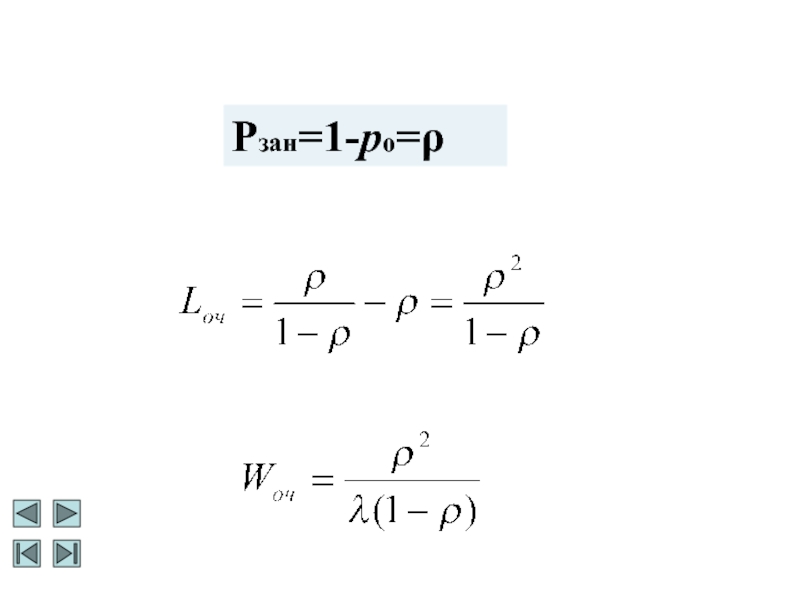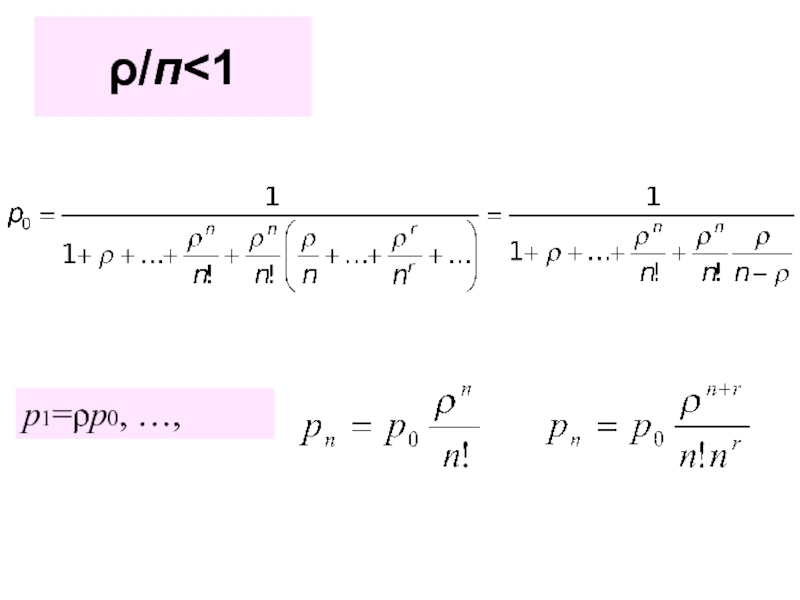Слайд 1Обнинский Институт Атомной Энергетики
Слайд 2Агнер Краруп Эрланг 1878-1929гг.,
родился в Дании
Пришел в Копенгагенскую Телефонную
Компанию в 1908 году как научный сотрудник и позднее глава
лаборатории
Применил теорию вероятности к проблемам телефонного трафика
Его первая работа была издана в 1909 году и доказывала, что телефонные звонки распределены беспорядочно во времени и подчиняются распределению Пуассона
Слайд 3Простейшие СМО
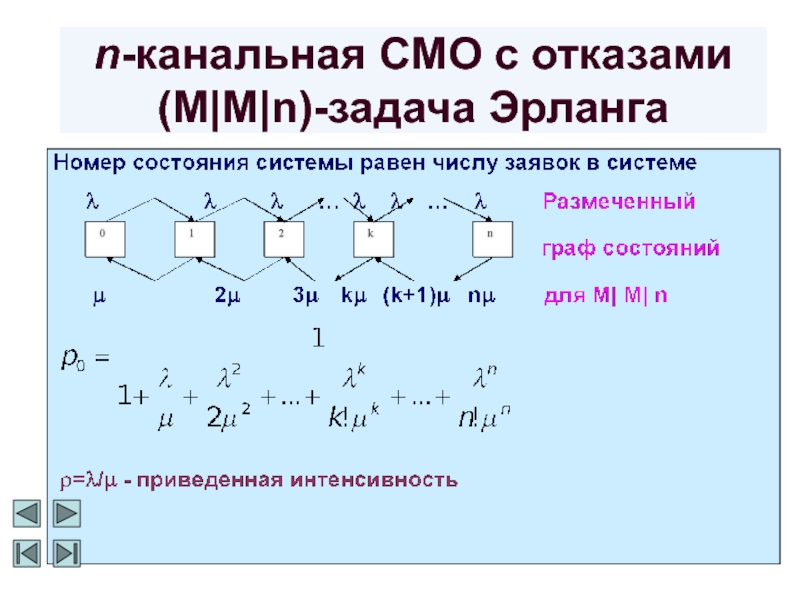
n-канальная СМО с отказами (M|M|n) - задача Эрланга
Слайд 4n-канальная СМО с отказами (M|M|n)-задача Эрланга
Слайд 7Пропускная способность
Q=1-Ротк –
относительная
A=λQ –
абсолютная
Показатели эффективности
n
p0 p1 p2 p3 …
pn
kср = 0 ⋅ pо + 1 ⋅ p1 + 2 ⋅ p2 + ... + n ⋅ pn
kср=A/μ
Показатели эффективности
Слайд 9
M|M|n - задача Эрланга
Пример
Станция связи с тремя каналами (n=3), интенсивность
потока заявок λ= 1,5 (заявки в минуту);
среднее время обслуживания
одной заявки tобсл=2 (мин),
все потоки событий - простейшие.
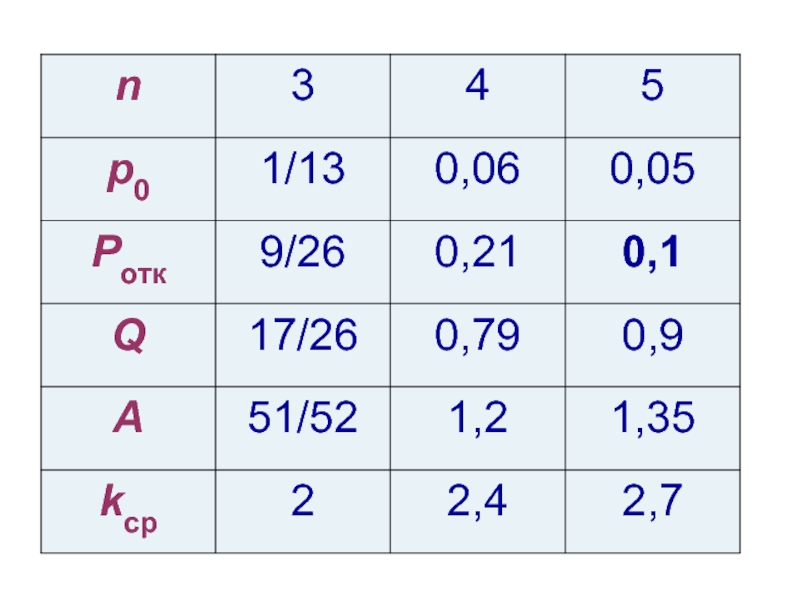
Найти финальные вероятности состояний и характеристики эффективности СМО: А, Q, Pотк , kср .
Слайд 10Пример 1. Имеется станция связи с тремя каналами (n=3),
интенсивность
входного потока λ= 1,5 заявки в минуту;
среднее время обслуживания
одной заявки tобсл=2 мин, все потоки событий − простейшие.
Найти финальные вероятности состояний и характеристики эффективности СМО: А, Q, Pотк , kср .
Найти число каналов, при котором вероятность отказа в обслуживании не превышает 0,1.
Слайд 14
p0=1-ρ
…
Как бы ни была нагружена система с очередью, если только
она вообще справляется с потоком заявок (ρ < 1),
самое вероятное число заявок в системе - 0.
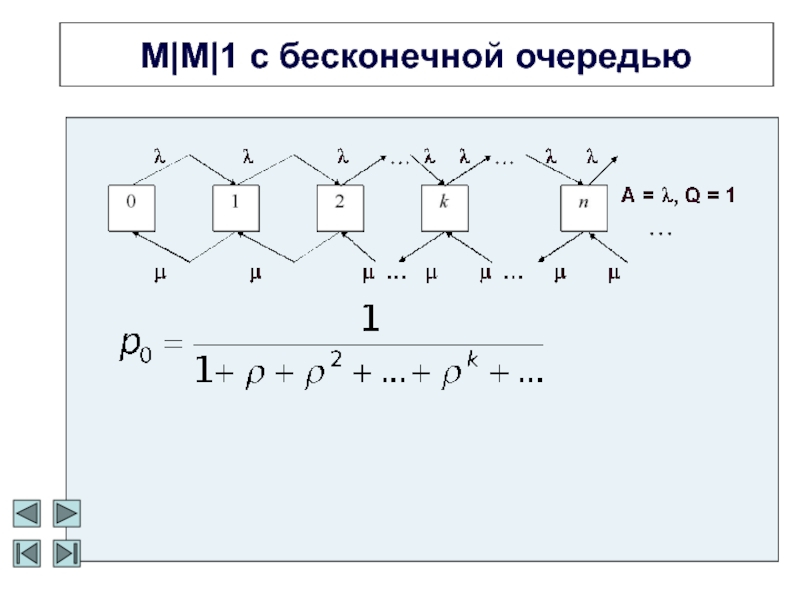
Слайд 15Одноканальная СМО с неограниченной очередью
Найдем среднее число заявок в СМО
Lсист .
Случайная величина Z — число заявок в системе
— имеет возможные значения 0, 1, 2, ..., k, ... с вероятностями р0 , p1, р2, ..., рk, ...
Слайд 17Пример
Одноканальная СМО - железнодорожная сортировочная станция, на которую поступает простейший
поток составов с интенсивностью λ=2 (состава в час).
Обслуживание (расформирование)
состава длится случайное показательное время со средним значением tобсл=20 мин.
В парке прибытия станции имеются два пути, на которых могут ожидать обслуживания прибывающие составы; если оба пути заняты, составы вынуждены ждать на внешних путях.
стац. режима работы станции):
среднее число составов Lсист, связанных со
станцией,
среднее время Wсист пребывания состава при станции (на внутренних путях, на внешних путях и под обслуживанием),
среднее число Lоч составов, ожидающих очереди на расформирование (все равно на каких путях),
среднее время Wоч пребывания состава в очереди,
среднее число составов, ожидающих расформирования на внешних путях Lвнеш и среднее время этого ожидания Wвнеш,
суммарный суточный штраф Ш, который придется заплатить станции за простои составов на внешних путях, если за один час простоя одного состава станция платит штраф а (руб.).
Слайд 19Решение
Интенсивность обслуживания μ=3 (состава/час), ρ=2/3,
Тогда
- Lсист=2
- Lоч=4/3 (состава)
Соответственно, по формулам Литтла Wсист=1 (час), Wоч=2/3 (час).
Очередь на внешних путях начинается с состояния номер 4 − и т.д.
Lвнеш= Lвнеш = 16/27 (состава), Wвнеш=8/27 (час).
Средний суточный штраф Ш за ожидание составов на внешних путях получим, перемножив среднее число составов, прибывающих на станцию за сутки, среднее время ожидания состава на внешних путях и часовой штраф а:
Ш=2*24*8/27*а=а*128/9)
Слайд 20Многоканальная СМО с неограниченной очередью
Номер состояния системы равен числу заявок
в системе:
S0 − в СМО заявок нет (все каналы свободны),
S1 − занят один канал, остальные свободны,
S2 − занято два канала, остальные свободны,
…
Sk − занято k каналов, остальные свободны,
Sn − заняты все п каналов (очереди нет),
Sn+1 − заняты все п каналов, одна заявка в очереди,
Sn+r − заняты все п каналов, r заявок стоит в очереди, …
Слайд 22Характеристики эффективности
Абсолютная пропускная способность СМО А равна среднему числу
заявок, поступающих в систему в единицу времени - λ
Среднее
число занятых каналов
kср =A/μ= ρ − это справедливо для любой СМО с неограниченной очередью
Найдем среднее число заявок в системе Lсист и среднее число заявок в очереди Lоч.
Lоч=
Lсист=Lоч+ρ
Деля выражения для Lоч и Lсист на λ, по формулам Литтла получим средние времена пребывания заявки в очереди и в системе.
Слайд 23Пример
Железнодорожная касса по продаже билетов с двумя окошками - двухканальная
СМО с неограниченной очередью, устанавливающейся сразу к двум окошкам.
Касса
продает билеты в два пункта: А и В. Интенсивность потока заявок для обоих пунктов А и В одинакова λА= λВ = 0,45, в сумме они образуют общий поток заявок с интенсивностью λА + λв = 0,9.
Кассир тратит на обслуживание пассажира в среднем 2 мин.
У кассы скапливаются очереди.
Предложение: вместо одной кассы, продающей билеты и в А, и в В, создать две специализированные кассы, продающие билеты одна - только в пункт А, другая - только в пункт В. Требуется проверить полезность предложения расчетом.
Все потоки событий – простейшие
Слайд 25Одноканальная СМО с ограниченной очередью
число заявок в очереди ограничено (не
может превосходить некоторого заданного m
Найти:
pi − финальные вероятности
состояний
Ротк − вероятность отказа,
А − абсолютную пропускную способность,
Рзан − вероятность того, что канал занят,
Lоч − среднюю длину очереди,
Lсист − среднее число заявок в СМО,
Wоч − среднее время ожидания в очереди,
Wсиcт − среднее время пребывания заявки в СМО .
Слайд 26Вер{канал занят}=1-Вер{канал свободен}=1− p0.
Pотк=Вер{заняты все места в
очереди}=pm+1=
Тогда относительная пропускная
способность
Q=1-Pотк=
Абсолютная пропускная способность А=λQ.
Слайд 27Пример 2. Банк принимает решение об открытии филиала, рассматривая его
как многоканальную систему с отказами.
Входной поток − простейший с
интенсивностью λ.
Производительность каждого канала μ.
Обслуживание одной заявки приносит средний доход С1. Создание одного канала обслуживания требует средних издержек С2, а эксплуатация одного канала в единицу времени − С3. Определить время τ, через которое филиал банка начнет приносить прибыль.
Слайд 28Решение. В стационарном режиме средний доход, приносимый СМО за время
τ,
D(τ) =АС1τ,
где А − абсолютная пропускная способность (среднее
число заявок, обслуживаемых СМО в единицу времени),
Аτ − среднее число заявок, обслуживаемых СМО за время τ.
А= μkср,
где kср − среднее число занятых каналов. Поэтому
D(τ) =С1μkсрτ
Средние издержки за это же время
Сср(τ)=С3kсрτ+С2n.
Слайд 29D(τ)=Сср(τ)
время, после которого СМО будет приносить прибыль,
Слайд 30 Пример 3.
При строительстве контакт-центра необходимо
оптимизировать количество операторских мест.
Для
этого нужно знать
среднюю продолжительность разговора,
среднее время поствызовной обработки,
среднее количество вызовов в час и
предпочтительный уровень обслуживания.
Слайд 31Пусть средняя продолжительность разговора равна 160 с, количество звонков –
240 в час,
время поствызывной обработки –
10 c,
уровень обслуживания – 80/20 (20% заявок получают отказ в обслуживании).
Решение. λ=240 звонков/ч=4 звонков/мин=1/15 зв./сек, интенсивность обслуживания μ=1/(160+10)сек=1/170 звонков/сек, ρ=λ/μ=170/15=34/3.
Pотк=0,2, отсюда следует, что среднее число занятых операторов (каналов)= ρ∙Q=0,8·34/3=9.
Поскольку уровень загрузки оператора должен быть примерно 75 % (оператор каждый час имеет перерыв 15 мин), то среднее количество операторов равно 12.
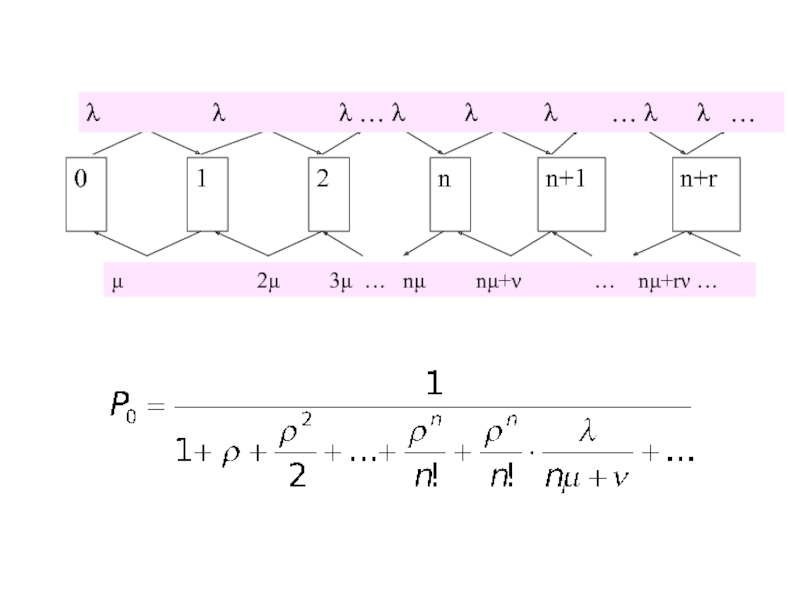
Слайд 32СМО с ограниченным временем ожидания
M/M/n, очередь бесконечна, но время пребывания
заявки в очереди ≤ Точ со средним значением tоч.
Тогда на каждую заявку, стоящую в очереди, действует как бы поток “уходов” с интенсивностью
Если этот поток – пуассоновский, то процесс в СМО – марковский.
2μ 3μ …
nμ nμ+ν … nμ+rν …
λ λ λ … λ λ λ … λ λ …
Слайд 35Замкнутые системы массового обслуживания
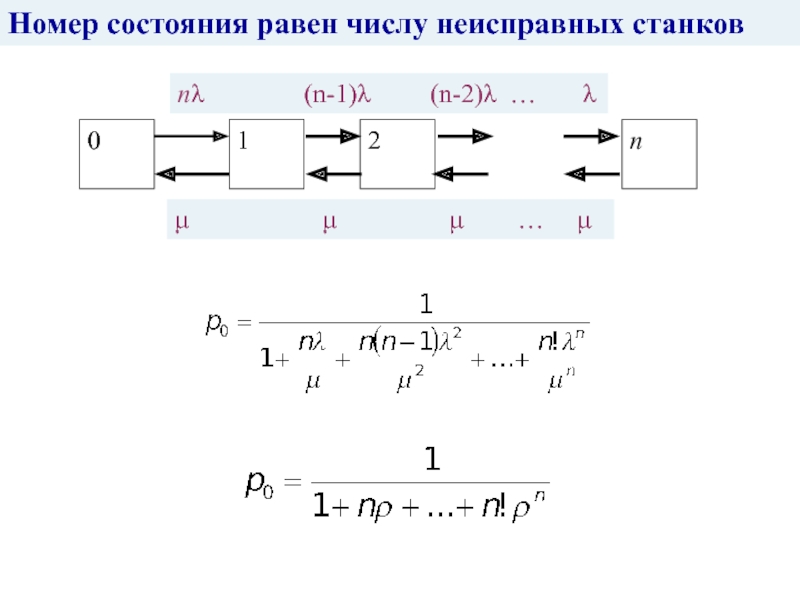
Рабочий-наладчик обслуживает n станков. Каждый станок может
с интенсивностью λ в любой момент выйти из строя и
потребовать обслуживания. Вышедший из строя станок останавливается. Если рабочий свободен, он берется за наладку станка, на это он тратит среднее время
t =1/μ,
где μ - интенсивность потока обслуживания (наладок).
Если рабочий занят, станок становится в очередь на обслуживание.
(n-2)λ … λ
μ
μ μ … μ
Номер состояния равен числу неисправных станков
Слайд 37 Абсолютная пропускная способность А –
это “среднее количество
заявок, прошедших через систему в единицу времени”,
в случае замкнутой
системы это
“среднее число неисправностей, устраняемых рабочим в единицу времени”.
Рабочий занят наладкой станка с вероятностью
Pзан=1-p0.
Если он занят, то обслуживает μ станков в единицу времени, значит, абсолютная пропускная способность системы
A=(1-p0)μ
Слайд 38Относительная пропускная способность Q=1, т.к. каждая заявка в конце концов
будет обслужена.
Среднее число неисправных станков ϖ найдем через абсолютную пропускную
способность: Каждый исправный станок порождает поток неисправностей с интенсивностью λ, в среднем работает (n-ϖ) станков, все неисправности устраняются рабочим, следовательно,
(n-ϖ)λ=(1-p0)μ,
откуда
,
или
ϖ=n-(1-p0)/ρ
Слайд 39Среднее число заявок в системе
Lсист=ϖ.
Среднее число заявок в очереди
Lоч=Lсист -Mν,
где ν - число станков на обслуживании.
Очевидно, что это случайная величина с рядом распределения
ее мат.ожидание Мν=1-p0.
Тогда Lоч=ϖ-(1-p0)=n-(1-p0)(1+1/ρ).
Зная среднее число неисправных станков ϖ и производительность q исправного станка в единицу времени, можно оценить среднюю потерю производительности группы станков в единицу времени за счет неисправностей
Q=qϖ.
Слайд 40Пример
Рабочий обслуживает группу из трех станков. Каждый станок останавливается в
среднем 2 раза в час. Процесс наладки занимает у рабочего
в среднем 10 мин. Определить характеристики замкнутой СМО:
вероятность занятости рабочего;
абсолютную пропускную способность А;
среднее количество неисправных станков;
среднюю относительную потерю производительности группы станков за счет неисправностей.
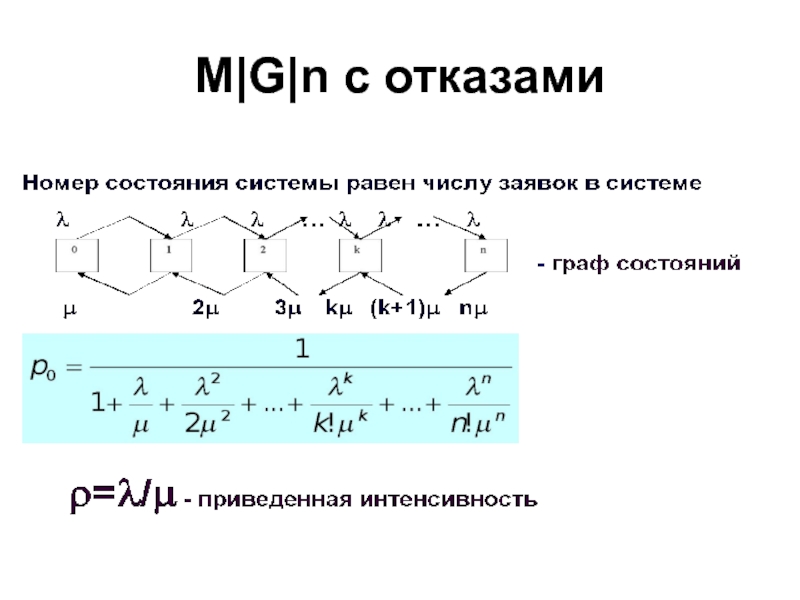
Слайд 41Немарковские СМО
n-канальная СМО с отказами,
с простейшим потоком заявок и
произвольным распределением
времени обслуживания
- M| G| n с
отказами -
Формулы Эрланга справедливы
и при произвольном распределении
времени обслуживания
Слайд 44Показатели эффективности
Пропускная способность
Q=1-Ротк – относительная
A=λQ – абсолютная
kср=A/μ - среднее число
занятых
каналов
Слайд 45Немарковские СМО
Одноканальная СМО
с неограниченной очередью, простейшим потоком заявок и
произвольным распределением
времени обслуживания
M| G| 1 с бесконечной
очередью
Слайд 46M| G| 1 с бесконечной очередью
Время обслуживания распределено по произвольному
закону
с мат. ожиданием tμ и
среднеквадратическим отклонением σμ
Коэффициент вариации
νμ= σμ/ tμ
Слайд 48M|M|1
Время обслуживания распределено по экспоненциальному закону
с мат. ожиданием tμ
и
среднеквадратическим отклонением σμ= tμ
Коэффициент вариации νμ= σμ/ tμ
=1!
Слайд 50M|D|1
Время обслуживания не является случайным – tμ,
среднеквадратическое отклонение σμ=0
Коэффициент
вариации νμ= σμ/ tμ =0!
Слайд 52Немарковские СМО
Одноканальная СМО
с произвольным потоком заявок и произвольным распределением
времени обслуживания
– G| G| 1 с ∞ очередью -
Слайд 53G| G| 1 с ∞ очередью
Время обслуживания распределено по произвольному
закону
с мат. ожиданием tμ =1/μ и
среднеквадратическим отклонением σμ
Коэффициент
вариации νμ= σμ/ tμ
0< νμ<1
Слайд 54G| G| 1 с ∞ очередью
Время между заявками распределено по
произвольному закону
с мат. ожиданием tλ=1/λ и
среднеквадратическим отклонением σλ
Коэффициент
вариации νλ = σλ / tλ
0< νλ<1
Слайд 55G|G|1 с бесконечной очередью
Неравенство Файнберга
Слайд 56Пример
В СМО поступают заявки в среднем через 15 мин, коэффициент
вариации равен 0,4.
Обслуживание происходит с интенсивностью 5 заявок в час,
коэффициент вариации времени обслуживания равен 0,7.
Оценить среднюю длину очереди
Слайд 57Пример
16/25*(0,16+0,49)*2,5-0,4*0,84
Слайд 58Пример
Если входной поток – простейший, то
Loch= 2,4
Loch = 16/25*(1+0,49)*2,5
Woch=2,4/4=0,6 ч=36
мин
Слайд 59Многоканальные немарковские СМО
Среднее число занятых каналов
kср=ρ
Слайд 60Многоканальные немарковские СМО
Если каналов много (по крайней мере >5),
то
поток обслуживания практически близок к простейшему.
Тогда можно использовать результаты
для системы М|M|n.
Слайд 61Многоканальные немарковские СМО
Когда входной поток заведомо не простейший
В этом случае можно подобрать две одноканальные СМО,
из которых одна по своей эффективности «лучше» данной многоканальной, а другая— «хуже» (очередь больше, время ожидания больше).
Слайд 62«Худший» вариант
(пессимистическая оценка)
n-канальную СМО на
п
одноканальных
На каждую СМО будет поступать
поток Эрланга п-го порядка
с коэффициентом вариации νλ =1/√n
Коэффициент вариации времени обслуживания – тот же G|G|1
…
λ
n
Слайд 63«Лучший» вариант
(оптимистическая оценка)
n-канальную СМО
одной
одноканальной,
но с интенсивностью потока обслуживания в n раз большей, чем у данной, т.е. равной пμ
ρ ? ρ´= ρ/n
Слайд 64Пример
Служба “Такси” хочет оптимизировать свою работу. Известно, что поток требований
на обслуживание имеет интенсивность λ=50 заявок/час, а время обслуживания распределено
по экспоненциальному закону с мат.ожиданием 15 мин. Затраты на содержание автомашин пропорциональны их количеству – С1=k1*n, а поступления - числу обслуженных заявок.
Определить необходимое количество автомашин в фирме, чтобы вероятность отказа в обслуживании не превышала 5%, а прибыль была максимальна.