Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проценты в заданиях ЕГЭ Решение заданий на проценты по материалам открытого
Содержание
- 1. Проценты в заданиях ЕГЭ Решение заданий на проценты по материалам открытого
- 2. Сотая часть числа называется процентом.1%20%25%50%
- 3. Чтобы выразить проценты в виде дроби, достаточно
- 4. Каждое число можно выразить в процентах.
- 5. Ключевые задачи на проценты
- 6. Налог на доходы составляет 13% от заработной
- 7. Цена на электрический чайник была повышена на
- 8. 3. Нахождение процентного отношения двух чисел Разделить
- 9. Задачи на нахождение процентов от числа и
- 10. Футболка стоила 800 рублей. После снижения цены она
- 11. Футболка стоила 800 рублей. После снижения цены она
- 12. Практические советы. 2. Закончив решать задачу, прочтите
- 13. №99565. В 2008 году в городском квартале
- 14. №99565. В 2008 году в городском квартале
- 15. №99570. Митя, Антон, Гоша и Борис учредили
- 16. Бизнесмен Бубликов получил в 2000 году прибыль
- 17. №99567. Четыре рубашки дешевле куртки на 8%.
- 18. №99568. Семья состоит из мужа, жены и
- 19. №99568. Семья состоит из мужа, жены и
- 20. №99568. Семья состоит из мужа, жены и
- 21. №99574. Виноград содержит 90% влаги, а изюм
- 22. Алгоритм вычисления сложных процентовВ банк вложена сумма
- 23. Алгоритм вычисления сложных процентовЕсли величину х уменьшить
- 24. №99566. В понедельник акции компании подорожали на
- 25. Цена холодильника в магазине ежегодно уменьшается на
- 26. №99571. В сосуд, содержащий 5 литров 12-процентного
- 27. №99572. Смешали некоторое количество 15-процентного раствора некоторого
- 28. Решение. Первый сплав: х кг – 100%Никель: ? кг
- 29. Решение. Первый раствор: х кг – 100%Кислота: ? кг
- 30. Решение. Четвертый раствор: 10 кг –
- 31. Решение. Первый раствор: 30 кг – 100%Кислота: ?
- 32. Решение. (продолжение)Для удобства возьмем каждого раствора по
- 33. Слайд 33
- 34. Слайд 34
- 35. Задача №17.1 марта 2010 года Аркадий взял в банке кредит под 10% годовых. Схема выплаты кредита следующая: 1 марта каждого
- 36. 17. Миша и Маша положили в один
- 37. Два брокера купили акции одного достоинства на
- 38. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Проценты в заданиях ЕГЭ
Решение заданий на проценты
по материалам открытого банка
задач ЕГЭ по математике
Слайд 3Чтобы выразить проценты в виде дроби, достаточно их число разделить
на 100 (в их числе перенести запятую на 2 знака
влево).300% = 3
90% = 0,9
9% = 0,09
36,7% = 0,367
0,9% = 0,009
Слайд 4Каждое число можно выразить в процентах. Для этого надо умножить
его на 100 и поставить знак %.
1 = 100%
0,07 =
7%0,7 = 70%
7 = 700%
0,007 = 0,7%
Слайд 6Налог на доходы составляет 13% от заработной платы.
Заработная плата
Ивана Кузьмича равна 12500 рублей.
Сколько рублей он получит после
вычета налога надоходы?
1 способ.
12500*0,13 = 1625
12500-1625 = 10875
2 способ
100%-13% = 87% = 0,87
12500*0,87 = 10875
Ответ . 10875
1. Нахождение процентов от числа
1) Перевести проценты в десятичную дробь.
2)Умножить число на полученную дробь.
Слайд 7Цена на электрический чайник была повышена на 16%
и составила
3480 рублей.
Сколько рублей стоил чайник до повышения цены?
Решение.
Цена была повышена
на 16%, то есть составила 116% = 1,16.3480 : 1,16 = 3000 (рублей).
Ответ. 3000.
2. Нахождение числа по его процентам
Перевести проценты в десятичную дробь.
Разделить число на полученную дробь.
Слайд 83. Нахождение процентного отношения двух чисел
Разделить первое число на второе.
Полученную
дробь умножить на 100%
В доме 700 квартир, причем 56 квартир
- трехкомнатные. Сколько процентов трехкомнатных квартир в доме?
Решение.
1). 56:700=0,08
2). 0,08·100=8%
Ответ 8%.
Слайд 9Задачи на нахождение процентов от числа и числа по его
процентам решаются с помощью пропорции.
Число А
– 100%Число В (часть числа А) – р%
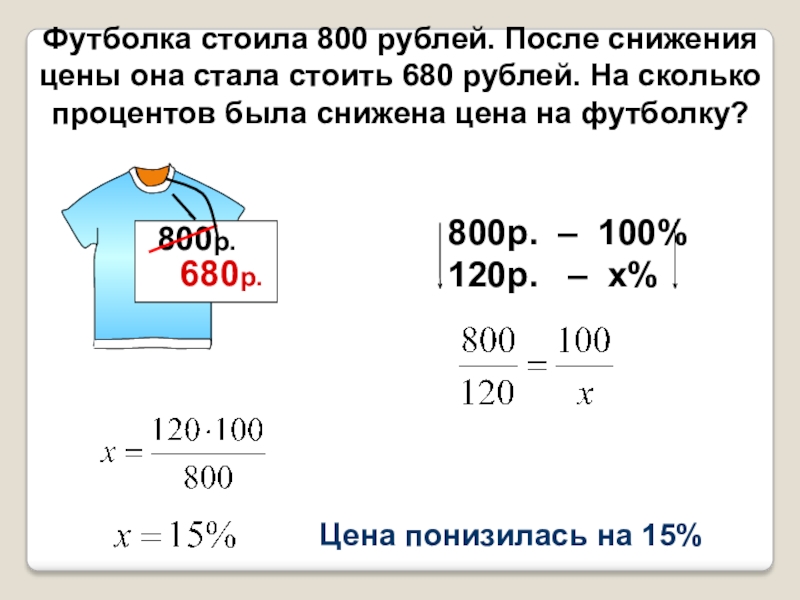
Слайд 10Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей.
На сколько процентов была снижена цена на футболку?
Новая цена составляет
85%, т.е. (т.к. 100%- 85%=15%)цена понизилась на 15%
800р. – 100%
680р. – х%
Слайд 11Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей.
На сколько процентов была снижена цена на футболку?
Цена понизилась на
15%
800р. – 100%
120р. – х%
Слайд 12Практические советы.
2. Закончив решать задачу, прочтите её ещё раз.
Вполне возможно,
найден промежуточный ответ, а не окончательный.
Внимательно читайте задачу.
1. Внимательно выбирайте величину, которую обозначите за 100%.
Слайд 13№99565. В 2008 году в городском квартале проживало 40000 человек.
В 2009 году, в результате строительства новых домов, число жителей
выросло на 8%, а в 2010 году − на 9% по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?Решение.
В 2008 году: 40 000 чел. – 100%
В 2009 году: х чел. – 108%
Откуда х = 40 000 · 108 /100 = 43 200 чел.
В 2009 году: 43 200 чел. – 100%
В 2010 году: у чел. – 109%
Откуда у = 43 200 · 109 /100 = 47 088 чел.
Ответ: 47 088.
Слайд 14№99565. В 2008 году в городском квартале проживало 40000 человек.
В 2009 году, в результате строительства новых домов, число жителей
выросло на 8%, а в 2010 году − на 9% по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?Решение.
Ответ: 47 088.
1). 40000 * 1,08 = 43200 жителей составит 108%
2009 г. - число жителей составит 108%
1,08
2010 г. - число жителей составит 109% от числа 43200,
2). 43200 * 1,09 = 47088 жителей составит 109%
1,09
2008 г. - 40000 человек.
Слайд 15№99570. Митя, Антон, Гоша и Борис учредили компанию с уставным
капиталом 200000 рублей. Митя внес 14% уставного капитала, Антон −
42000 рублей, Гоша − 0,12 уставного капитала, а оставшуюся часть капитала внес Борис. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли 1000000 рублей причитается Борису? Ответ дайте в рублях.Решение.
Уставной капитал: 200000 руб. – 100%
Митя: – 14%
Гоша: – 12%
Антон: 42000 руб. –
Борис: остальное –
Антон внес: 42000 · 100 /200000 = 21% уставного капитала.
Тогда Борис внес 100 – (14 + 12 + 21) = 53% уставного капитала.
Таким образом, от прибыли 1 000 000 рублей Борису
причитается 1000000 · 53 /100 = 530000 рублей.
Ответ: 530 000.
53%
21%
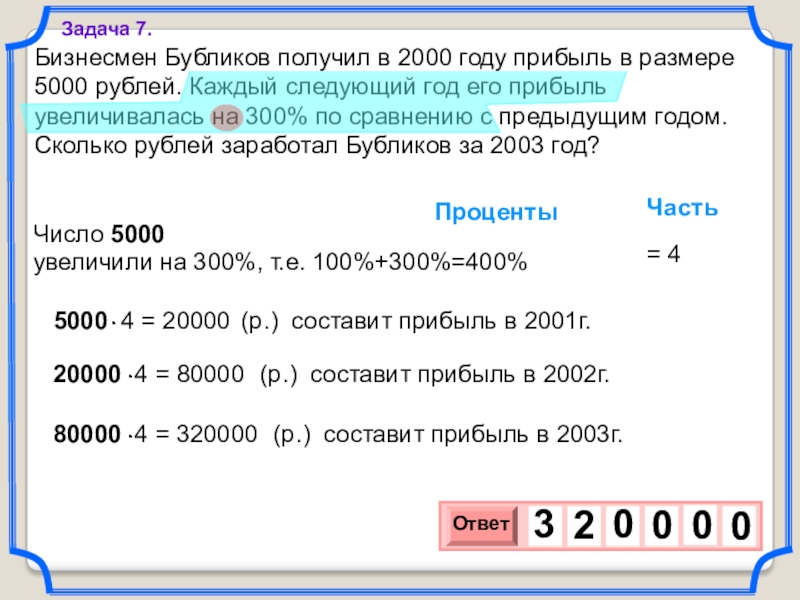
Слайд 16Бизнесмен Бубликов получил в 2000 году прибыль в размере 5000
рублей. Каждый следующий год его прибыль увеличивалась на 300% по
сравнению с предыдущим годом. Сколько рублей заработал Бубликов за 2003 год?Задача 7.
увеличили на 300%, т.е. 100%+300%=400%
Число 5000
Проценты
Часть
= 4
(р.) составит прибыль в 2001г.
(р.) составит прибыль в 2002г.
(р.) составит прибыль в 2003г.
Слайд 17№99567. Четыре рубашки дешевле куртки на 8%. На сколько процентов
пять рубашек дороже куртки?
Решение.
Пусть х руб. – стоимость
одной рубашки, тогда 4х – 92% от стоимости куртки
х – 23% от стоимости куртки
5х – 115% от стоимости куртки,
что на 15% дороже самой куртки
Ответ: 15.
Слайд 18№99568. Семья состоит из мужа, жены и их дочери студентки.
Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос
бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?Решение. (1 способ)
Пусть х% – составляет зарплата мужа,
У% – зарплата жены
z% – стипендия дочери, тогда общий доход семьи
⇒ х = 67%
100
=
│ ×3
⇒ х + у + z + 2x + 2y = 288
=
100
х + у + z/3 = 96.
2х + у + z = 167
х + у + z = 100
Слайд 19№99568. Семья состоит из мужа, жены и их дочери студентки.
Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос
бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?Ответ: 27.
Решение. (продолжение)
Слайд 20№99568. Семья состоит из мужа, жены и их дочери студентки.
Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос
бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?Ответ: 27.
Решение. (2 способ)
То, что если бы зарплата мужа увеличилась вдвое, а общий доход семьи вырос бы на 67%, означает, что зарплата мужа составляет 67% дохода семьи.
То, что если бы стипендия дочери уменьшилась втрое и при этом общий доход семьи сократился бы на 4%, означает, что доля уменьшения (а именно - две трети ее стипендии) составляет 4% дохода семьи, одна треть 2% дохода семьи, и тем самым вся ее стипендия - 6%.
Таким образом, муж и дочь вместе получают доход 67%+6%=73% , а жена соответственно 100%-73%=27%
Слайд 21№99574. Виноград содержит 90% влаги, а изюм − 5%. Сколько
килограммов винограда требуется для получения 20 килограммов изюма?
Решение.
Виноград: х кг
– 100%Влага: – 90%
Сухое вещество: ? кг – 10%
Откуда ? = 10 · х /100 = 0,1х кг – сухого вещества в винограде
Изюм: 20 кг – 100%
Влага: – 5%
Сухое вещество: 0,1х кг – 95%
Откуда 0,1х · 100 = 20 · 95
х = 190 кг – винограда
Ответ: 190.
Слайд 22Алгоритм вычисления сложных процентов
В банк вложена сумма х рублей под
р % годовых.
Через год сумма увеличится на
Сумма станет
через годчерез 2 года
через n лет
Слайд 23Алгоритм вычисления сложных процентов
Если величину х уменьшить на р процентов,
получим:
Если величину увеличить на p процентов, получим:
Если величину х сначала
увеличить на р процентов, а затем уменьшить на q процентов, получим соответственно:
Слайд 24№99566. В понедельник акции компании подорожали на некоторое число процентов,
а во вторник подешевели на то же самое число процентов.
В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?Пусть a - стоимость акции до начала торгов в понедельник.
Решение.
(1+0,01х)
a
(1–0,01х)
стоимость акции во вторник, после торгов в процессе повышения и понижения на х %,
будет составлять разовое понижение на 4%,
a
(1–0,04)
=
:a
(1+0,01х)(1-0,01х)=0,96
1 – 0,0001х2 = 0,96
10000-х2=9600
х2=400
х=20
Ответ: 20
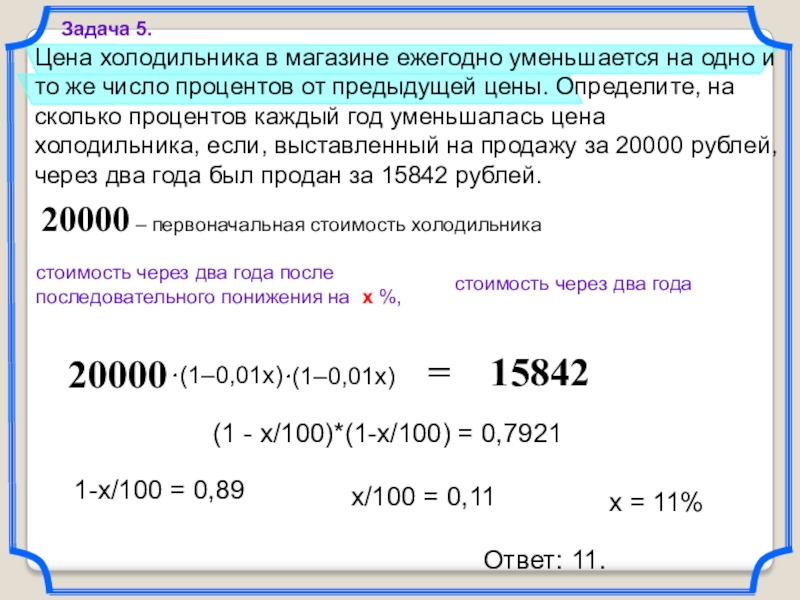
Слайд 25Цена холодильника в магазине ежегодно уменьшается на одно и то
же число процентов от предыдущей цены. Определите, на сколько процентов
каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20000 рублей, через два года был продан за 15842 рублей.Задача 5.
20000
15842
стоимость через два года после последовательного понижения на х %,
стоимость через два года
=
20000 – первоначальная стоимость холодильника
(1 - x/100)*(1-x/100) = 0,7921
1-x/100 = 0,89
x/100 = 0,11
x = 11%
Ответ: 11.
Слайд 26№99571. В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого
вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося
раствора?Решение.
Весь раствор: 5 л – 100%
Вещество: х л – 12%
Откуда х = 5· 12 /100 = 0,6 л – вещества в растворе
Весь раствор: 5 + 7 л – 100%
Вещество: 0,6 л – у%
Откуда у = 0,6 · 100 /12 = 5%
Ответ: 5.
Слайд 27№99572. Смешали некоторое количество 15-процентного раствора некоторого вещества с таким
же количеством 19-процентного раствора этого вещества. Сколько процентов составляет концентрация
получившегося раствора?Решение.
Первый раствор: х – 100%
Вещество: ? – 15%
Откуда ? = 15 · х /100 = 0,15х – вещества в I растворе
Второй раствор: х – 100%
Вещество: ? – 19%
Откуда ? = 19 · х /100 = 0,19х – вещества во II растворе
Третий раствор: 2х – 100%
Вещество: 0,15х + 0,19х – у%
Откуда у = 0,34х · 100 /2х = 17% – концентрация нового раствора
Ответ: 17.
Слайд 28Решение.
Первый сплав: х кг – 100%
Никель: ? кг – 10%
Откуда
? = 10 · х /100 = 0,1х кг –
никеля в I сплаве.Второй сплав: 200 – х кг – 100%
Никель: ? кг – 30%
Откуда ? = 30 · (200 – х) /100 = 0,3(200 – х) кг – никеля во II сплаве.
Третий сплав: 200 кг – 100%
Никель: 0,1х + 0,3(200 – х) кг – 25%
Получаем уравнение: 200 · 25 = (0,1х + 0,3(200 – х)) · 100, откуда х = 50 кг – никеля в I сплаве; 200 – 50 = 150 кг – масса второго сплава; значит, масса первого сплава на 150 – 50 = 100 кг меньше.
Ответ: 100.
№99575. Имеется два сплава. Первый содержит 10% никеля, второй − 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Слайд 29Решение.
Первый раствор: х кг – 100%
Кислота: ? кг – 30%
Откуда
? = 30 · х /100 = 0,3х кг –
кислоты в I растворе.Второй раствор: у кг – 100%
Кислота: ? кг – 60%
Откуда ? = 60 · у /100 = 0,6у кг – кислоты во II растворе.
Третий раствор: х + у + 10 кг – 100%
Кислота: 0,3х + 0,6у кг – 36%
Получаем 1-ое уравнение: (х + у + 10) · 36 = (0,3х + 0,6у) · 100.
№99577. Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Слайд 30Решение.
Четвертый раствор: 10 кг – 100%
Кислота: ?
кг – 50%
Откуда ? = 50
· 10 /100 = 5 кг – кислоты в IV растворе.Пятый раствор: х + у + 10 кг – 100%
Кислота: 0,3х + 0,6у + 5 кг – 41%
Получаем 2-ое уравнение: (х + у + 10) · 41 = (0,3х + 0,6у + 5) · 100.
Составим систему уравнений:
№99577. Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Ответ: 60.
Слайд 31Решение.
Первый раствор: 30 кг – 100%
Кислота: ? кг – х%
Откуда ? = 30 · х /100 = 0,3х кг
– кислоты в I растворе.Второй раствор: 20 кг – 100%
Кислота: ? кг – у%
Откуда ? = 20 · у /100 = 0,2у кг – кислоты во II растворе.
Третий раствор: 50 кг – 100%
Кислота: 0,3х + 0,2у кг – 68%
Получаем 1-ое уравнение: (0,3х + 0,2у) · 100 = 50 · 68.
№99578. Имеется два сосуда. Первый содержит 30 кг, а второй − 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Слайд 32Решение. (продолжение)
Для удобства возьмем каждого раствора по 10 кг:
Четвертый раствор: 20
кг – 100%
Кислота: 0,1х + 0,1у
кг – 70%Получаем 2-ое уравнение: (0,1х + 0,1у) · 100 = 20 · 70.
Составим систему уравнений:
0,3 · 60 = 18 кг – кислоты в первом сосуде.
№99578. Имеется два сосуда. Первый содержит 30 кг, а второй − 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Ответ: 18.
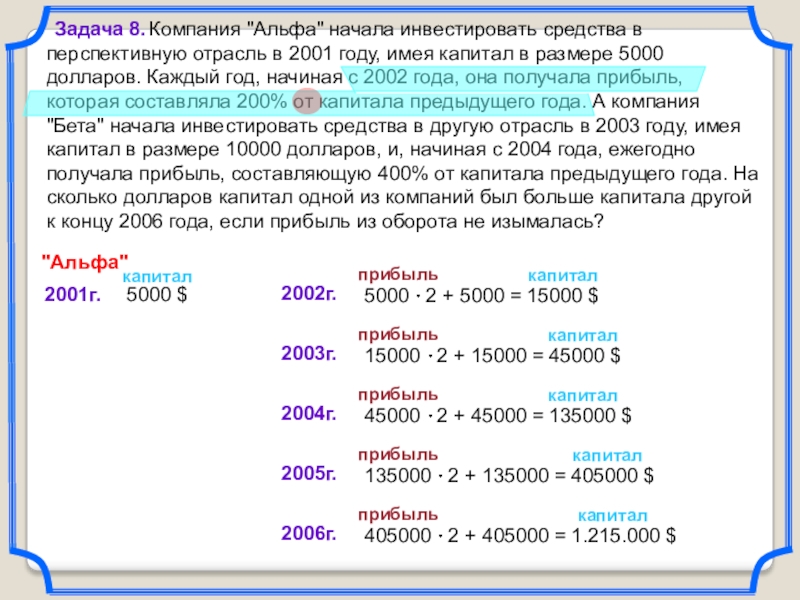
Слайд 33
Компания "Альфа" начала инвестировать средства в перспективную отрасль
в 2001 году, имея капитал в размере 5000 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 200% от капитала предыдущего года. А компания "Бета" начала инвестировать средства в другую отрасль в 2003 году, имея капитал в размере 10000 долларов, и, начиная с 2004 года, ежегодно получала прибыль, составляющую 400% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2006 года, если прибыль из оборота не изымалась?Задача 8.
капитал
Слайд 34
Компания "Альфа" начала инвестировать средства в перспективную отрасль
в 2001 году, имея капитал в размере 5000 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 200% от капитала предыдущего года. А компания "Бета" начала инвестировать средства в другую отрасль в 2003 году, имея капитал в размере 10000 долларов, и, начиная с 2004 года, ежегодно получала прибыль, составляющую 400% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2006 года, если прибыль из оборота не изымалась?Задача 8.
1250.000 – 1215000 = 35000
Слайд 35Задача №17.
1 марта 2010 года Аркадий взял в банке кредит под 10% годовых.
Схема выплаты кредита следующая: 1 марта каждого следующего года
банк начисляет
проценты на оставшуюся сумму долга (то есть увеличивает долг на 10 %), затем Аркадий переводит в банк платёж. Весь долг Аркадий
выплатил за 3 платежа, причем второй платеж оказался в два раза больше
первого, а третий в три раза больше первого. Сколько рублей взял в кредит Аркадий, если за три года он выплатил банку 2395800 рублей?
Решение.
Пусть А руб –
сумма кредита, х – первый, 2х – второй, 3х – третий платеж.За три года выплачено х+2х+3х=2 395 800 руб., откуда
Сумма долга 1 марта 2011 года - 1,1 А (увеличен на 10%)
1 марта 2012 года –
1 марта 2013 года –
По условию задачи:
Преобразуя к виду
Ответ. 1923000 руб.
Х=399 300.
3х+2,2х+1,21х=1,331А
Слайд 3617. Миша и Маша положили в один и тот же
банк одинаковые суммы под 10% годовых. Через год сразу после
начисления процентов Миша снял со своего счета 5000 рублей, а еще через год снова внес 5000 рублей. Маша, наоборот, через год доложила на свой счет 5000 рублей, а еще через год сразу после начисления процентов сняла со счета 5000 рублей. Кто через три года со времени первоначального вложения получит большую сумму и на сколько рублей?Слайд 37Два брокера купили акции одного достоинства на сумму 3640 р.
Когда цена на эти акции возросла, они продали часть акций
на сумму 3927 р. Первый брокер продал 75% своих акций, а второй – 80% своих. При этом сумма от продажи акций, полученная вторым брокером, на 140% превысила сумму, полученную первым брокером. На сколько процентов возросла цена одной акции?Решение.
Пусть первый брокер купил акции на сумму х рублей, а второй - у рублей. Тогда х+у=3640 (1)
Первый брокер продал 75% своих акций за 0,75х*р рублей,
а второй 80% акций, купленных за 0,8у рублей, продал за 0,8х*р рублей.
Т.о. 0,75рх + 0,8ру = 3927 (2).
Составим пропорцию:
0,75рх - 100%
0,8ру - 240%
0,75рх*240 = 0,8ру*100 ==> 9x=4y или х=4у/9 подставим в (1):
4у/9 +у = 3640; у=2520; х=3640-2520=1120
х, у - деньги, вложенные в акции.
Подставим х и у в уравнение (2):
0,75р*1120 + 0,8р*2520 =3927
840р+2016р = 3927
2856р=3927, р=3927/2856 =1,375
Каждая акция подорожала в 1,375 раз, что соответствует 137,5%.
137,5%-100%=37,5%.
Ответ: 37,5