Слайд 2Классификация прямых
Прямые общего положения – это прямые, непараллельные и
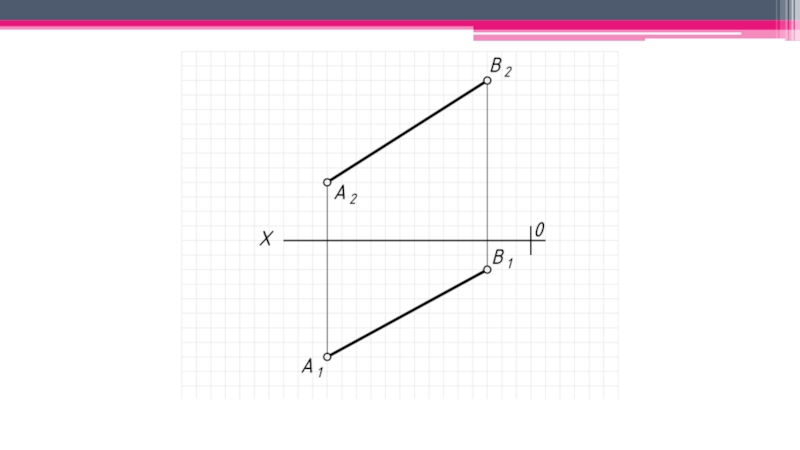
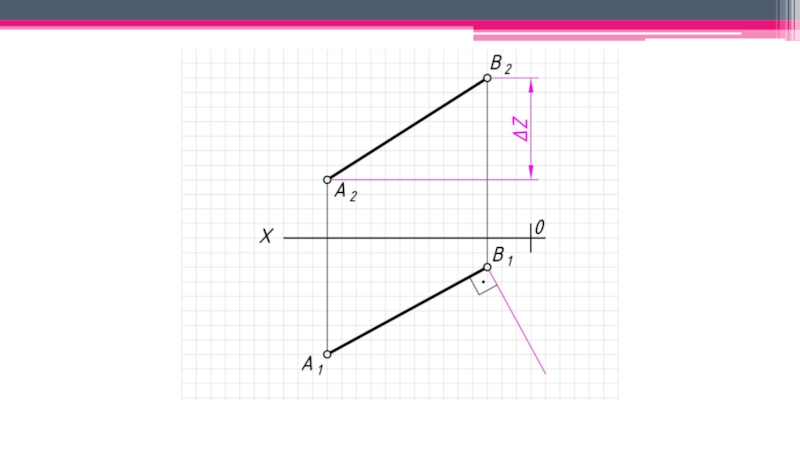
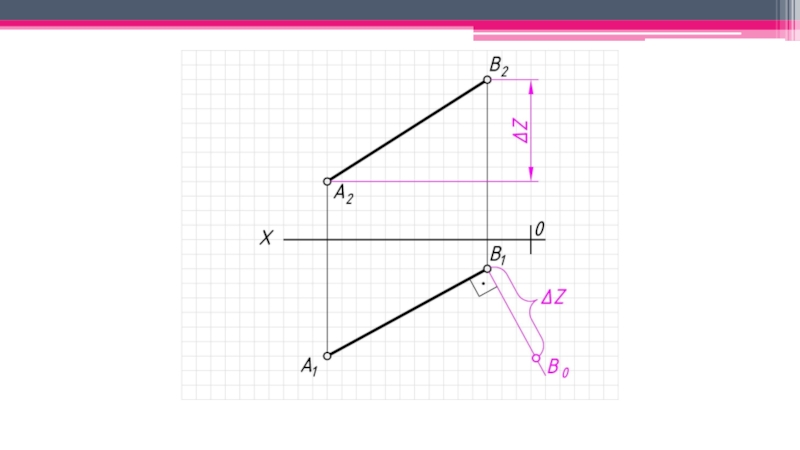
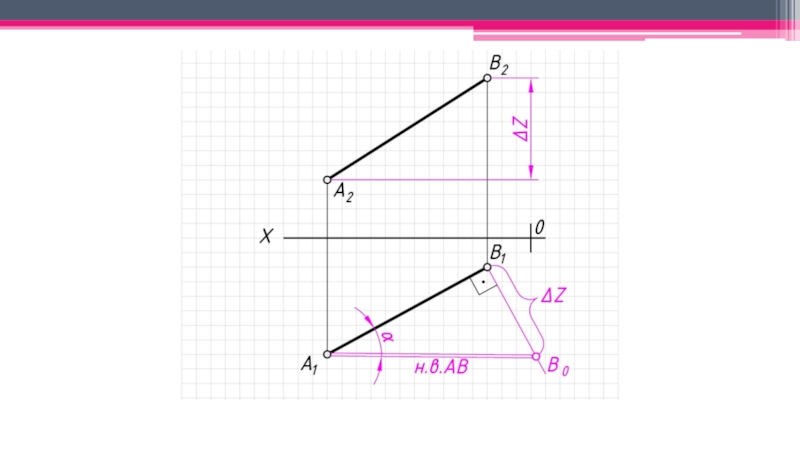
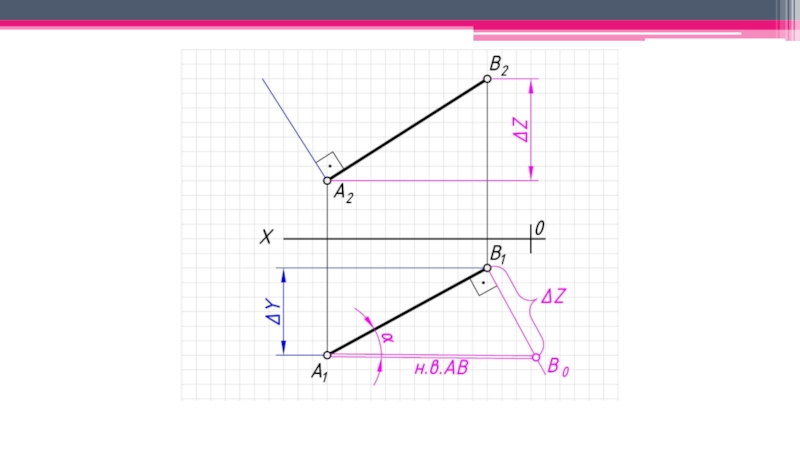
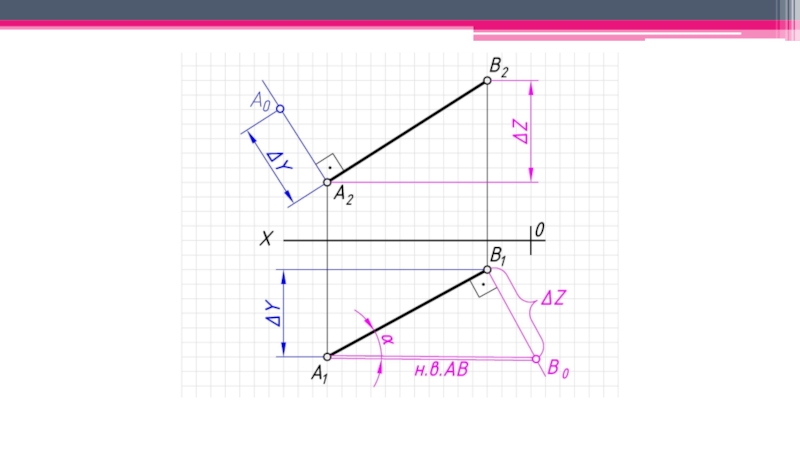
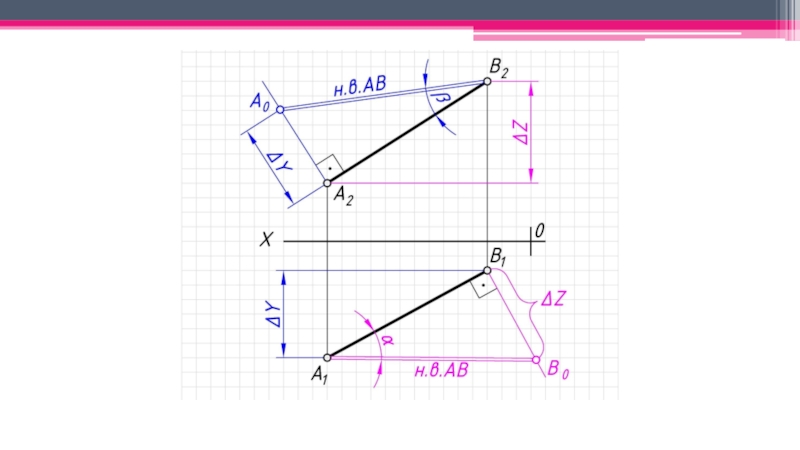
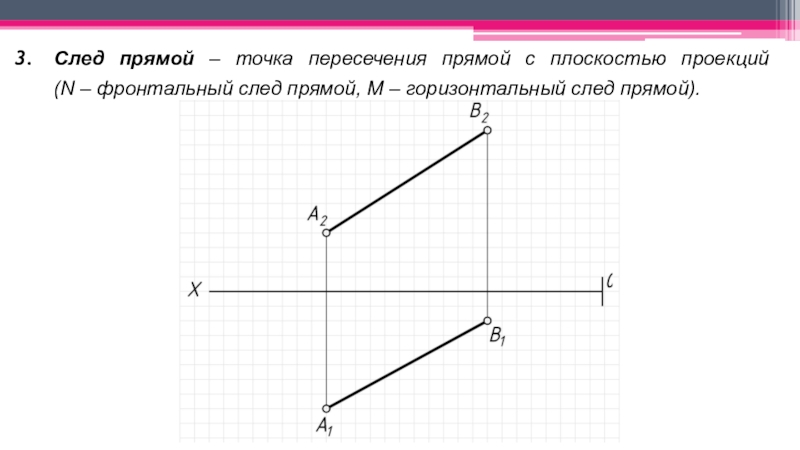
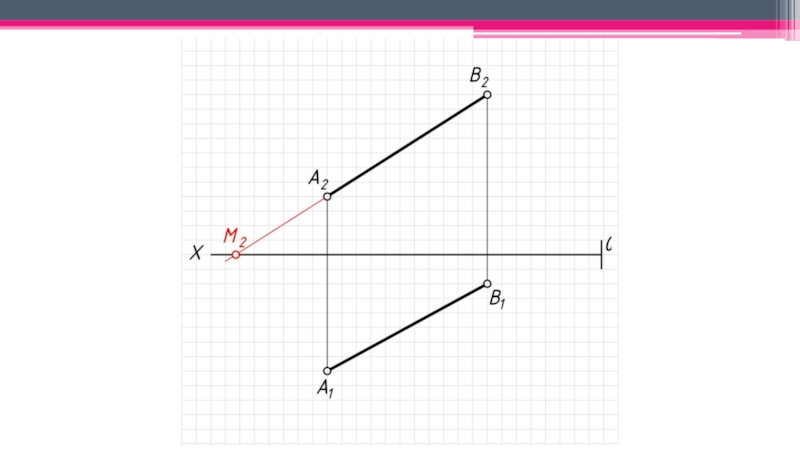
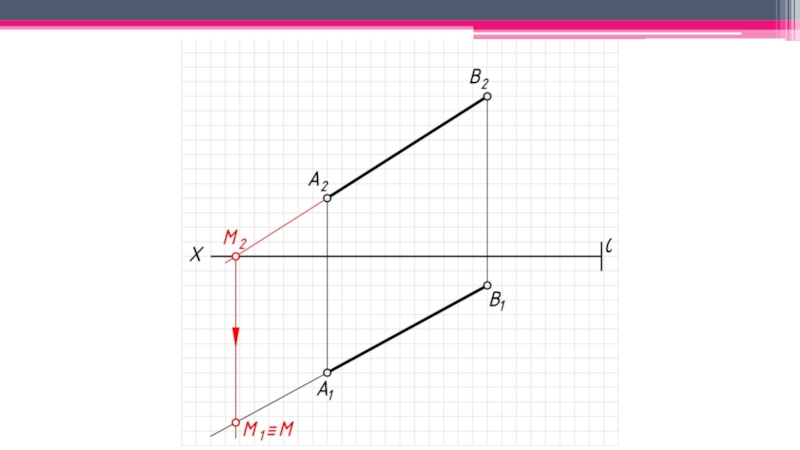
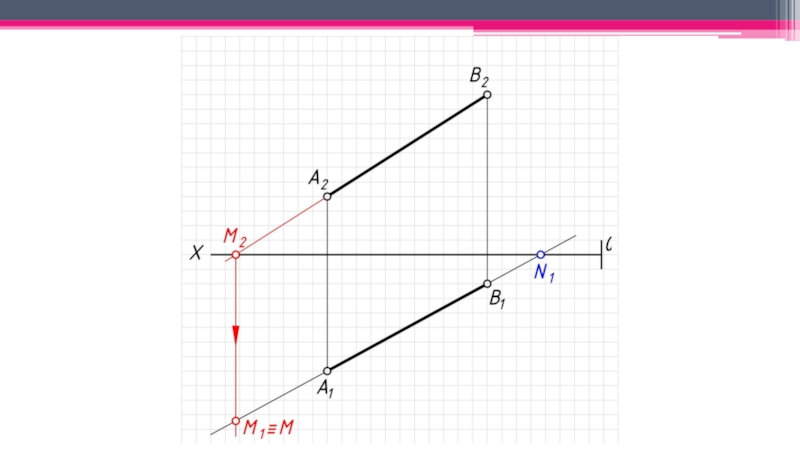
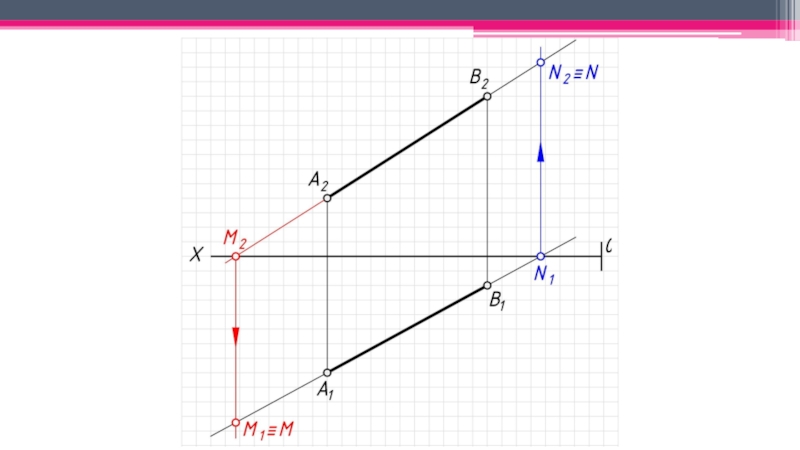
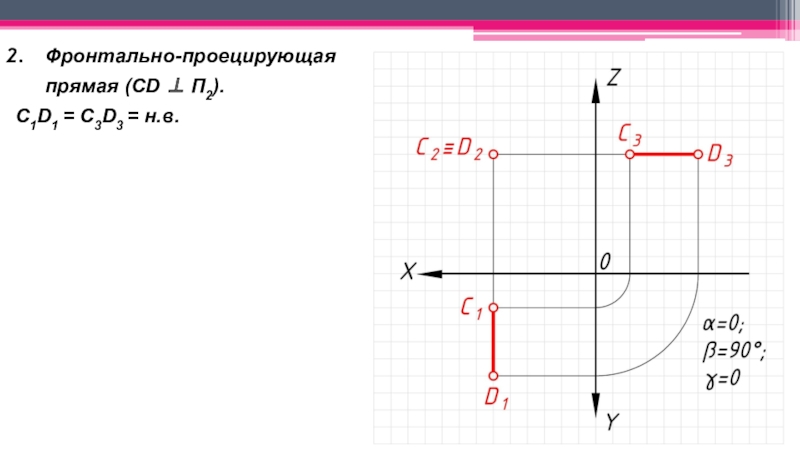
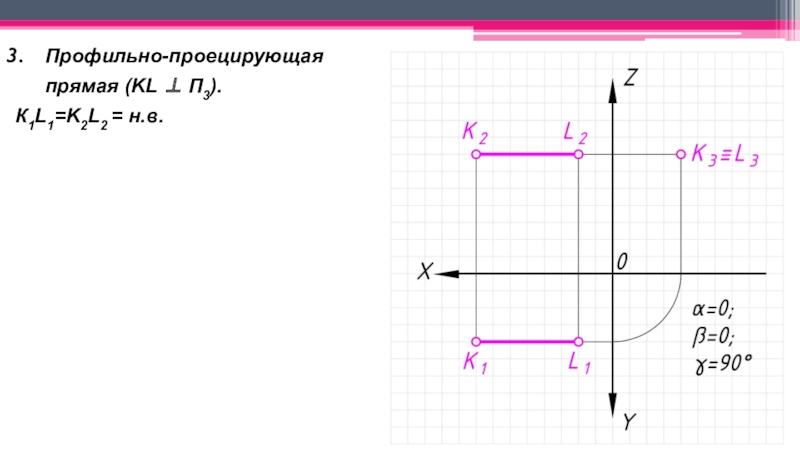
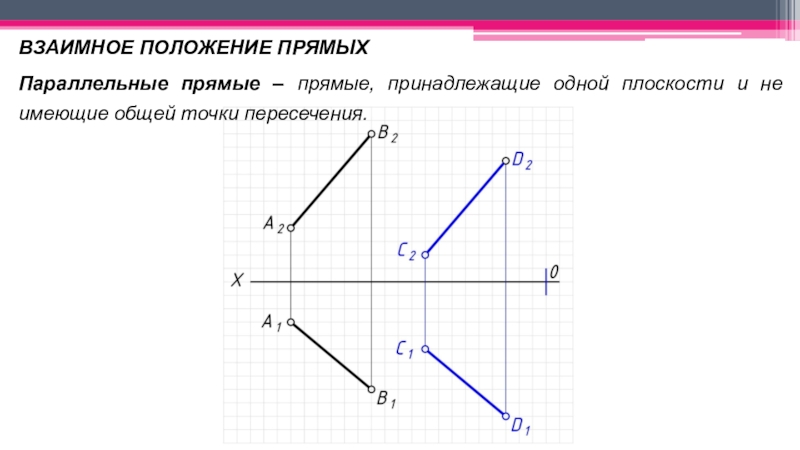
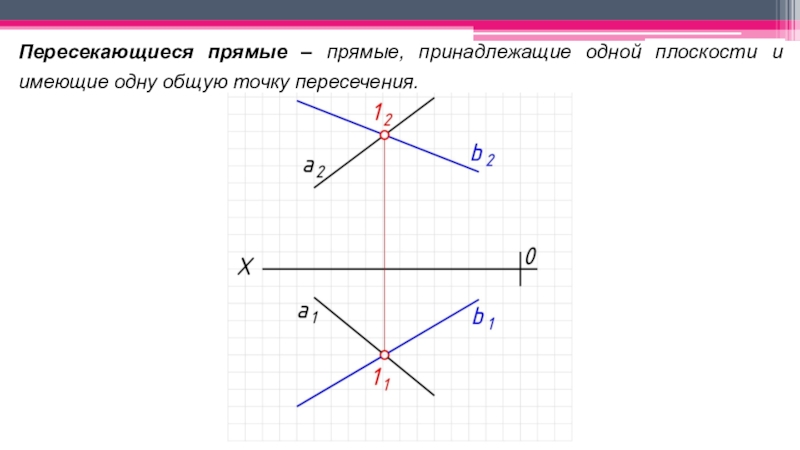
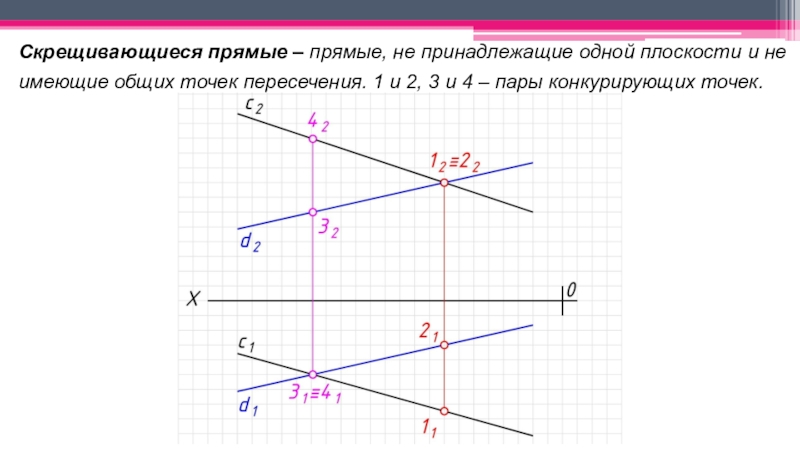
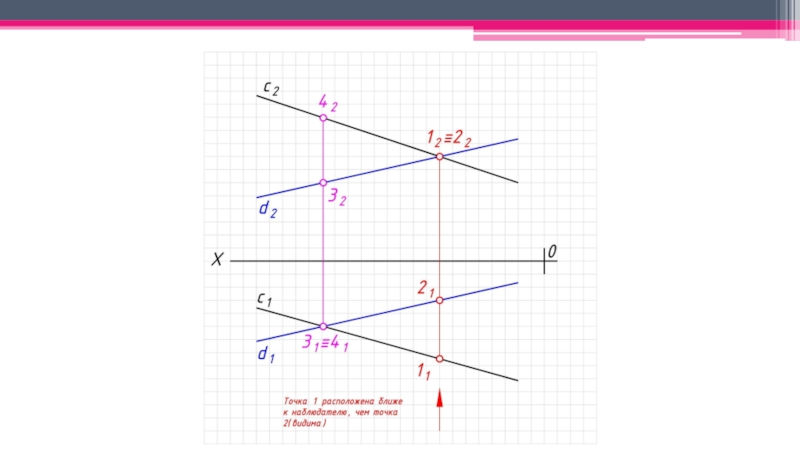
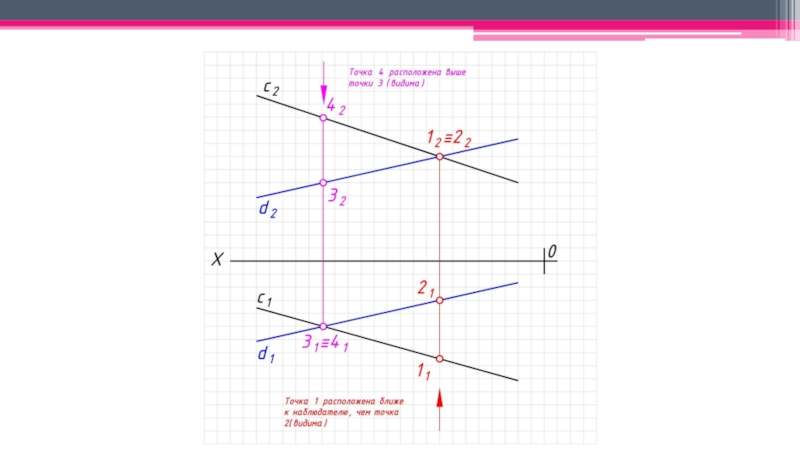
неперпендикулярные ни одной из плоскостей проекций.
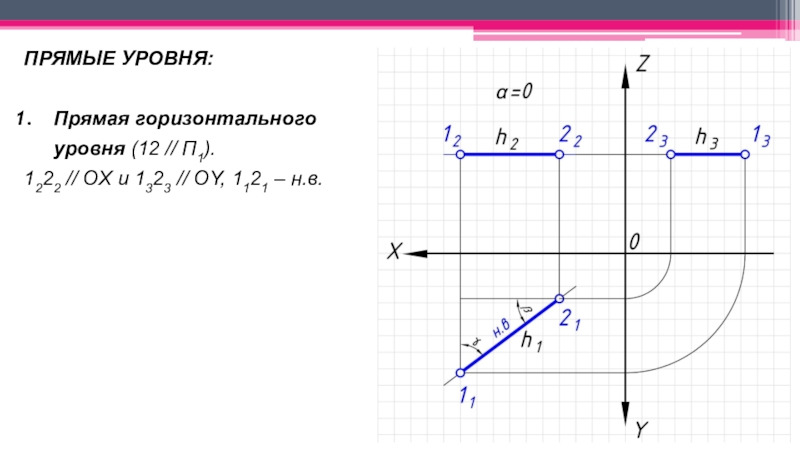
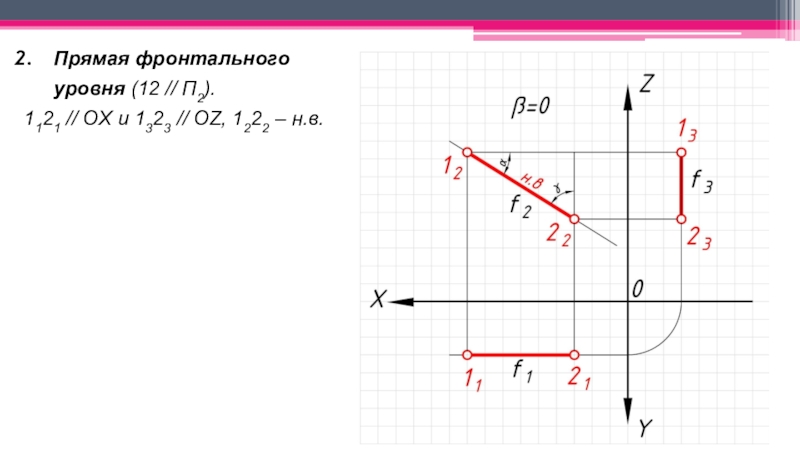
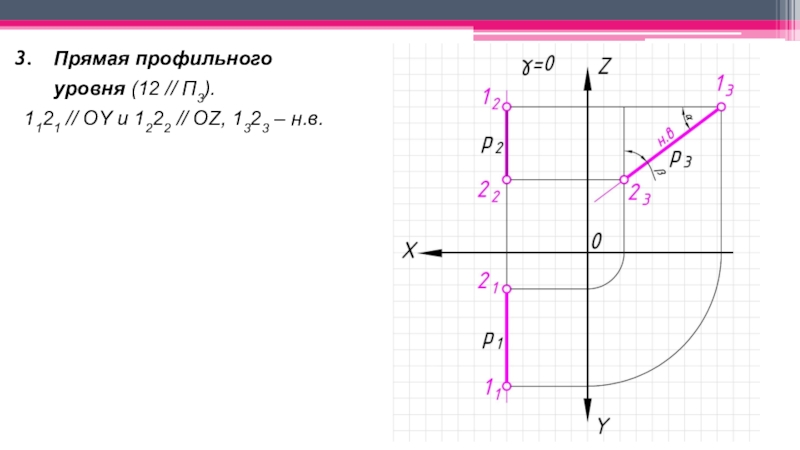
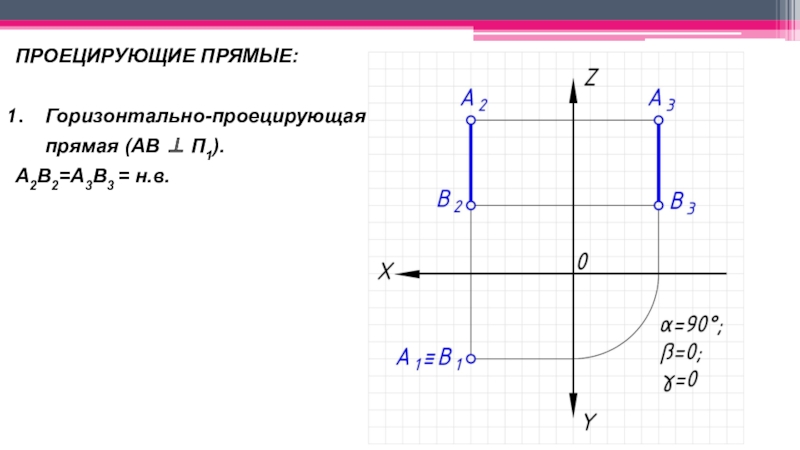
Прямые частного положения:
Уровня – параллельные
одной из плоскостей проекций и не перпендикулярные двум другим;
Проецирующие – перпендикулярные к одной плоскости проекций и параллельные двум другим.
Слайд 3Позиционно-метрические свойства прямой:
Натуральная величина прямой – определяется способом прямоугольного треугольника.
Угол
наклона отрезка прямой к соответствующей плоскости проекций является угол между
его проекцией на данную плоскость и натуральной величиной рассматриваемого отрезка.
Слайд 11След прямой – точка пересечения прямой с плоскостью проекций
(N
– фронтальный след прямой, M – горизонтальный след прямой).
Слайд 16Принадлежность точки прямой.
Теорема: Если в пространстве точка принадлежит прямой, то
на чертеже одноименные проекции точки принадлежат одноименным проекциям прямой.
Теорема: Если
в пространстве точка делит отрезок прямой в каком-то отношении, то на чертеже проекции этой точки делят одноименные проекции отрезка в том же отношении.
Слайд 17Принадлежность точки прямой.
Теорема: Если в пространстве точка принадлежит прямой, то
на чертеже одноименные проекции точки принадлежат одноименным проекциям прямой.
Теорема: Если
в пространстве точка делит отрезок прямой в каком-то отношении, то на чертеже проекции этой точки делят одноименные проекции отрезка в том же отношении.
Слайд 18ПРЯМЫЕ УРОВНЯ:
Прямая горизонтального
уровня (12 // П1).
1222 // OX и 1323
// OY, 1121 – н.в.
Слайд 19Прямая фронтального
уровня (12 // П2).
1121 // OX и 1323 //
OZ, 1222 – н.в.
Слайд 20Прямая профильного
уровня (12 // П3).
1121 // OY и 1222 //
OZ, 1323 – н.в.
Слайд 21ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ:
Горизонтально-проецирующая прямая (АВ П1).
A2B2=A3B3 = н.в.
Слайд 22Фронтально-проецирующая прямая (CD П2).
С1D1 = C3D3 = н.в.
Слайд 23Профильно-проецирующая прямая (KL П3).
К1L1=K2L2 = н.в.
Слайд 24ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ
Параллельные прямые – прямые, принадлежащие одной плоскости и
не имеющие общей точки пересечения.
Слайд 25Пересекающиеся прямые – прямые, принадлежащие одной плоскости и имеющие одну
общую точку пересечения.
Слайд 26Скрещивающиеся прямые – прямые, не принадлежащие одной плоскости и не
имеющие общих точек пересечения. 1 и 2, 3 и 4
– пары конкурирующих точек.
