Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема. Разложение положительной обыкновенной дроби в конечную десятичную дробь
Содержание
- 1. Тема. Разложение положительной обыкновенной дроби в конечную десятичную дробь
- 2. До сих пор мы рассматривали десятичные дроби,
- 3. Конечные десятичные дроби всегда можно записать в
- 4. Сократили на 25
- 5. Сократили на 4
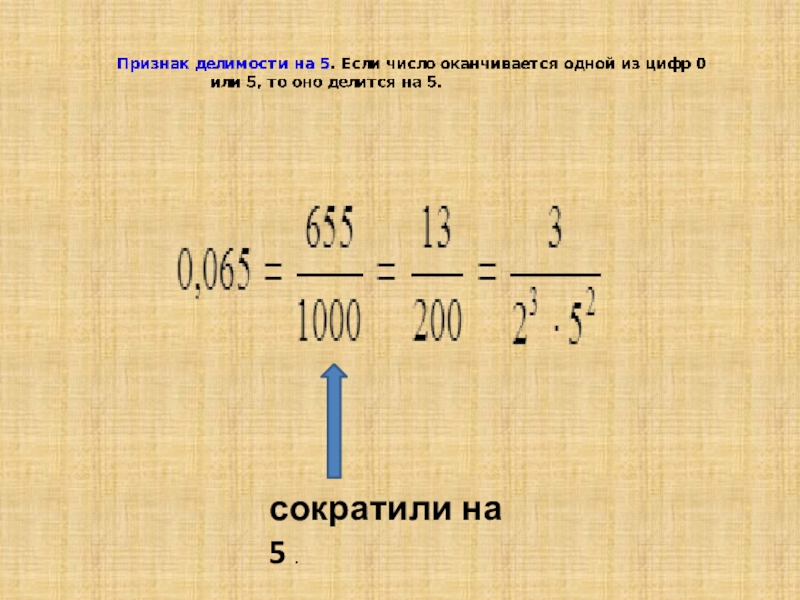
- 6. сократили на 5 .
- 7. Из этих примеров видно, чтоПравило. Если конечную
- 8. Верно и обратное утверждение.Правило. Если знаменатель q
- 9. Для разложения обыкновенной несократимой дроби, знаменатель которой
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Решение упражнений. Уч.с.190 № 959(3 стл.). Какие
- 14. Разложение на простые множители надо показать: н-р:
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. УГОЛОК ПИСАТЬ!
- 20. УГОЛКИ писать!
- 21. Скачать презентанцию
До сих пор мы рассматривали десятичные дроби, которые называют конечными, потому что после запятой у них стоит конечное число цифр. В дальнейшем мы будем рассматривать и бесконечные десятичные дроби. У них после
Слайды и текст этой презентации
Слайд 2До сих пор мы рассматривали десятичные дроби, которые называют конечными,
потому что после запятой у них стоит конечное число цифр.
дальнейшем мы будем рассматривать и бесконечные десятичные дроби. У них после запятой бесконечно много цифр.Слайд 3 Конечные десятичные дроби всегда можно записать в виде обыкновенных дробей.
Пример
1. Представьте конечную десятичную дробь в виде несократимой обыкновенной дроби
и разложить знаменатель на простые множители:Слайд 7Из этих примеров видно, что
Правило. Если конечную десятичную дробь записать
в виде обыкновенной несократимой дроби , то ее знаменатель q
не имеет других простых делителей, кроме 2 и 5.Слайд 8Верно и обратное утверждение.
Правило. Если знаменатель q несократимой дроби не
имеет других простых делителей, кроме 2 и 5, то эта
дробь разлагается в конечную десятичную дробь.Слайд 9 Для разложения обыкновенной несократимой дроби, знаменатель которой не имеет других
простых делителей, кроме 2 и 5 в конечную десятичную дробь,
существует два способа. Один из них сводится к умножению числителя и знаменателя дроби на соответствующую степень числа 2 или числа 5.Другой способ деление числителя на знаменатель уголком.
Слайд 13Решение упражнений.
Уч.с.190 № 959(3 стл.). Какие простые множители содержит знаменатель
дроби:
в) Ответ: 2 и
7. ж) Ответ: 2.
л) Ответ: 2 и 5.