Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА С ДУГАМИ
Содержание
- 1. ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА С ДУГАМИ
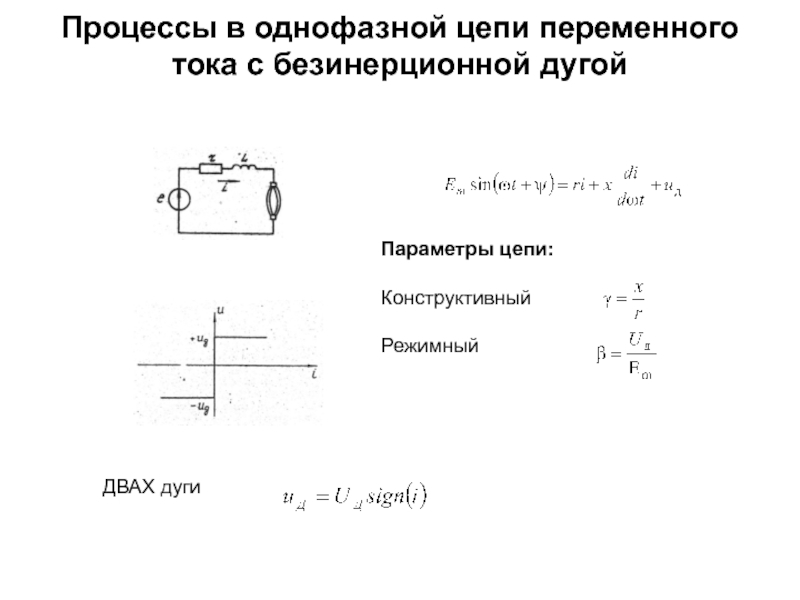
- 2. Процессы в однофазной цепи переменного тока с безинерционной дугой Параметры цепи: КонструктивныйРежимныйДВАХ дуги
- 3. Слайд 3
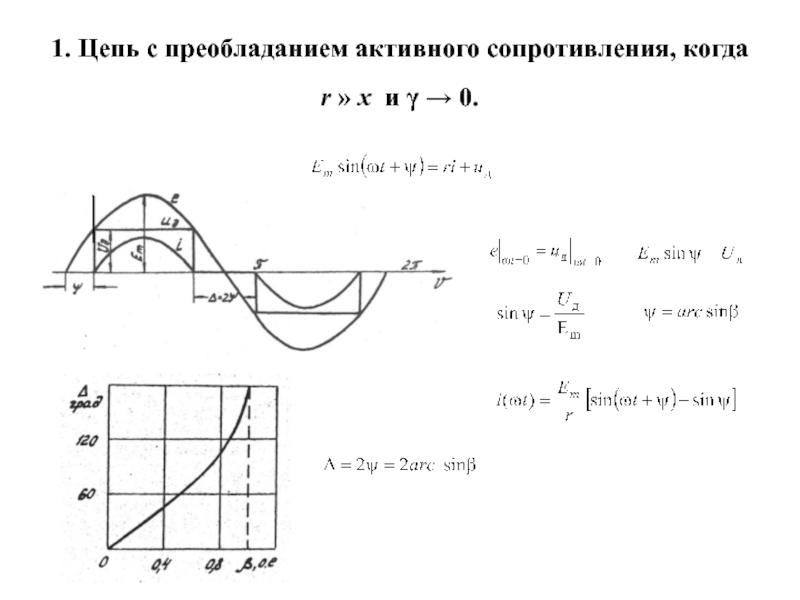
- 4. 1. Цепь с преобладанием активного сопротивления, когда r » x и γ → 0.
- 5. 2. Цепь с преобладанием реактивного сопротивления, когда r
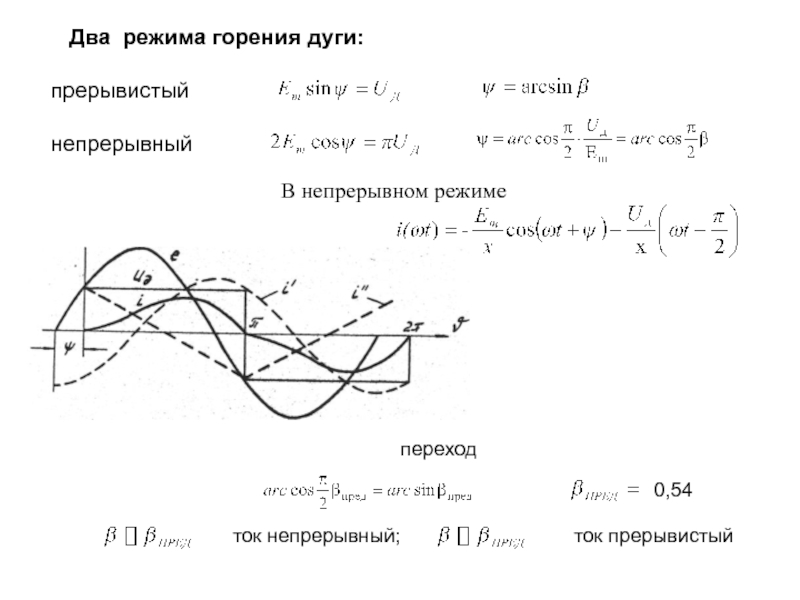
- 6. Два режима
- 7. 3. Соизмеримые значения активного и реактивного сопротивленийРешим
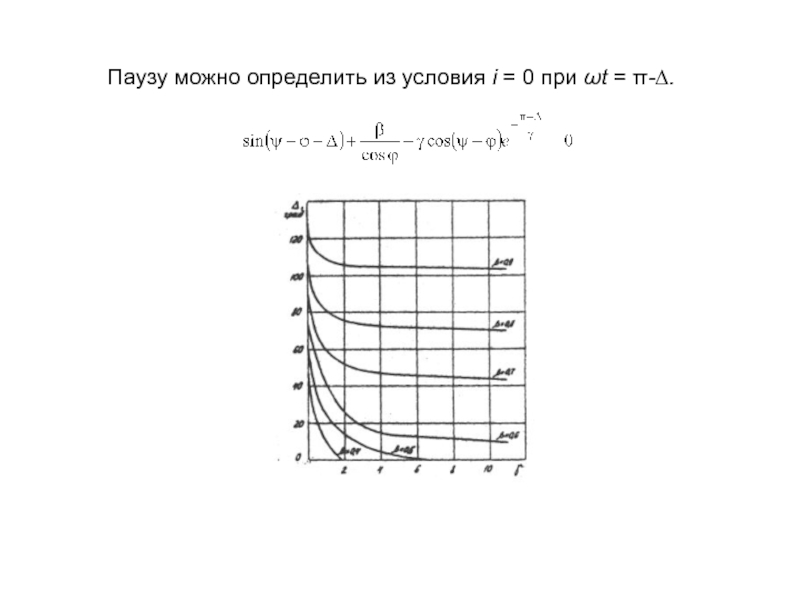
- 8. Паузу можно определить из условия i = 0 при ωt = π-∆.
- 9. Определим переход от непрерывного к прерывистому режиму, приравняв ∆ = 0. В результате
- 10. Можно вывести выражения для мощности дуги. В
- 11. Метод гармонического анализа Он основан на замене
- 12. Мгновенное значение токагде φ = arc tg
- 13. Не смотря на то, что начальные фазы
- 14. Зачастую эта ДВАХ ближе к реальным условиям,
- 15. Процессы в трехфазной симметричной цепи
- 16. - группа нулевой последовательности - это гармоники
- 17. Произведем расчет цепи для
- 18. Как и в однофазной цепи, дуга может
- 19. Условия повторного зажигания дуги Общее условие однофазная цепьтрехфазная цепь
- 20. Приравняв выражения
- 21. Ток дуги в трехфазной цепи имеет значительно
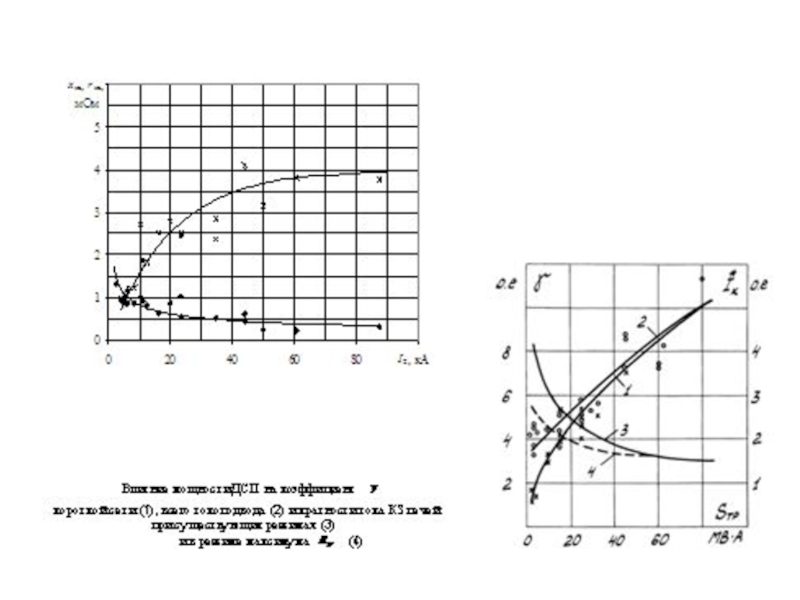
- 22. Кривые напряжения дуги (1), напряжения между нулевыми
- 23. Определим мощность дуговой печи. Полная мощность, потребляемая
- 24. .Тогда можно определить электрический КПД печи.Учитывая, что
- 25. Влияние инерционности дуги на процессы в электрических
- 26. Влияние инерционности дуги на βпредВлияние инерционности душ
- 27. Влияние формы динамической ВАХ дуги на процессы
- 28. Разложение в ряд Фурье напряжения имеет вид
- 29. Влияние параметров динамической ВАХ на значение βпред:
- 30. Скачать презентанцию
Слайды и текст этой презентации
Слайд 52. Цепь с преобладанием реактивного сопротивления, когда r
и γ → ∞
Зажигание дуги происходит при условии
Слайд 6 Два режима горения дуги:
прерывистый
непрерывный
переход
0,54
ток
непрерывный;ток прерывистый
В непрерывном режиме
Слайд 73. Соизмеримые значения активного и реактивного сопротивлений
Решим неоднородное дифференциальное уравнение
Принужденный
режим
где
Свободный
режим
Из условия зажигания дуги (ωt = 0, i = 0)
Слайд 10Можно вывести выражения для мощности дуги. В общем случае она
равна
Для непрерывного режима это выражение упрощается
Анализ однофазной
цепи с дугой методом решения дифференциального уравнения позволяет получить точное решение для мгновенного значения тока. Однако определение действующих значений тока и напряжения сопряжено с определенными вычислительными трудностями. Сложно оценить и степень несинусоидаль-ности кривых. Слайд 11Метод гармонического анализа
Он основан на замене по методу компенсации
нелинейной дуги несинусоидальной ЭДС с последующим разложением ее кривой в
ряд Фурье. Таким образом, цепь линеаризуется и применим метод наложения. Рассмотрим метод гармонического анализа на примере непрерывного режима цепи r, L с характерными параметрами β и γ.Для случая представления ВАХ дуги в виде функции иД = UДsign i напряжение дуги представляет собой периодическую функцию прямоугольной формы. Из-за ее симметричности относительно центра координат в разложении в ряд отсутствуют четные гармоники
.
Линеаризованная цепь производятся для каждой гармоники отдельно комплексным методом:
Слайд 12Мгновенное значение тока
где φ = arc tg nγ (кроме первой
гармоники, для которой угол φ1 зависит
не только от γ,
но и от начальной фазы ЭДС источника ψ).Угол ψ определяется из условия i(0)=0
Действующие значения тока и напряжения определяются по выражениям:
В непрерывном режиме действующее напряжение дуги U равно напряжению горения UД. При появлении паузы действующее значение напряжения дуги меньше напряжения ее горения.
Активная мощность дуги определяется как
Слайд 13Не смотря на то, что начальные фазы мгновенных значений тока
и напряжения дуги совпадают, активная мощность дуги меньше полной мощности
дуги SД = IU. Это связано не с реактивностью дуги, а с несинусоидальностью тока и напряжения и появлением мощности искажения Метод гармонического анализа наряду с серьезными преимуществами имеет и недостатки.
Одним из них является снижение точности расчетов из-за замены бесконечного ряда конечным числом гармоник.
Второй недостаток имеет методический характер. Известно, что разрывная функция f(x), в таковой является прямоугольная форма напряжения дуги, при разложении в ряд, при переходе через разрыв (х = 0,π...), делает скачок примерно на 18% больший, чем исходная функция. Это явление называется эффектом Гиббса . В результате представление напряжения дуги рядом Фурье в окрестности точек разрыва не вполне удовлетворительно. При этом получаемая динамическая ВАХ дуги несколько отличается от теоретической.
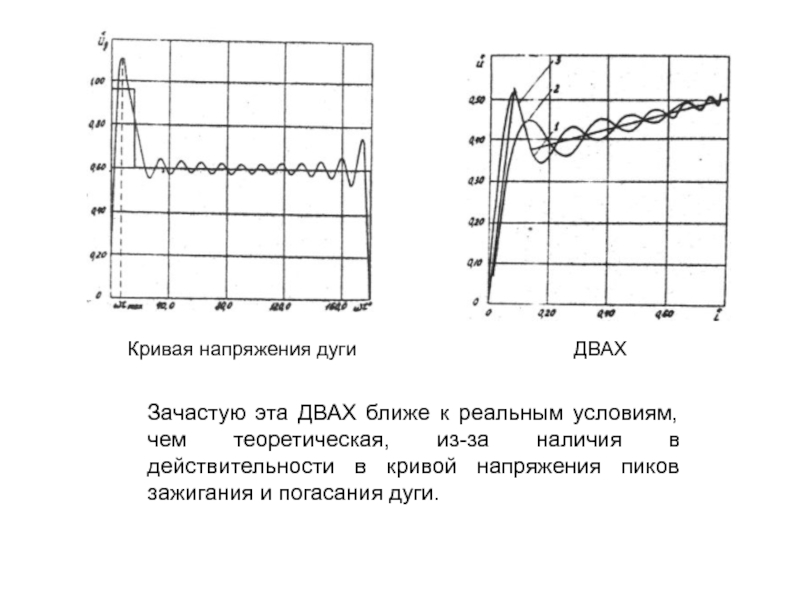
Слайд 14Зачастую эта ДВАХ ближе к реальным условиям, чем теоретическая, из-за
наличия в действительности в кривой напряжения пиков зажигания и погасания
дуги.ДВАХ
Кривая напряжения дуги
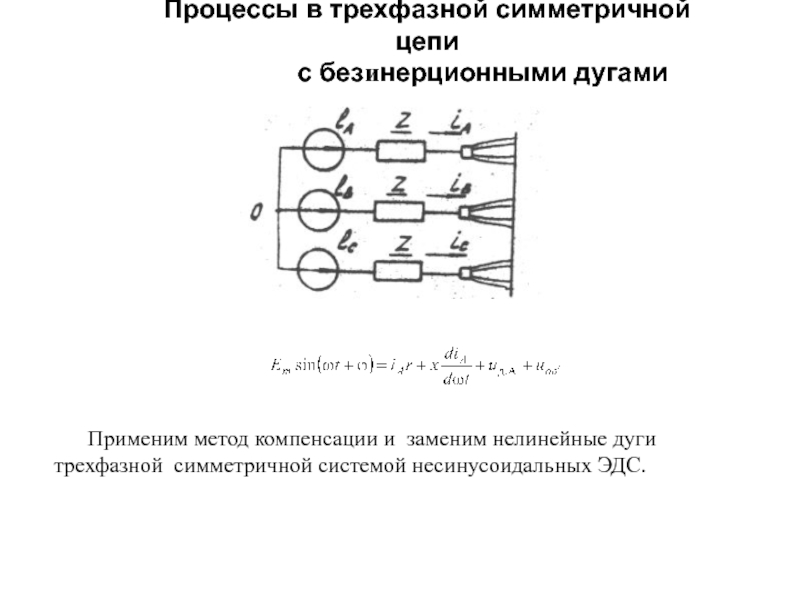
Слайд 15Процессы в трехфазной симметричной цепи
с безинерционными дугами
Применим метод
компенсации и заменим нелинейные дуги трехфазной симметричной системой несинусоидальных ЭДС. ;
Слайд 16- группа нулевой последовательности - это гармоники с номерами
п = 3k («кратные трем») (п = =0.3, 9, 15...).
Для этих гармоник ЭДС всех фаз имеют одну и ту же начальную фазу.Как известно, при применении гармонического анализа такая трехфазная система может быть разделена на три группы гармоник с разной последовательностью фаз:
- группа прямой последовательности - это гармоники с номерами
п = 3k + 1, они имеют в симметричной трехфазной системе прямую последовательность фаз, т.е. ЭДС фазы В отстает от ЭДС фазы А на
а ЭДС фазы С опережает ее на
К этой последовательности относится основная (первая) гармоника, а также седьмая, тринадцатая и т.д.;
- группа обратной последовательности - это гармоники с номерами п = 3k -1 (п = 5, 11, 19...). Эти гармоники имеют обратную последовательность фаз, т.е. фаза В не отстает, а опережает фазу А на
Слайд 17 Произведем расчет цепи для каждой группы последовательностей.
При этом ввиду симметричности схемы все гармоники прямой и обратной
последовательностей напряжения сдвига нейтрали u00′ равны нулю, а гармоники токов, кратные трем, в цепи отсутствуют.Тогда
Мгновенное значение тока
Слайд 18Как и в однофазной цепи, дуга может гореть непрерывно или
прерывисто. При непрерывном режиме начальная фаза ЭДС фазы А определяется
из уравнения i (0) = 0, пауза отсутствует.В прерывистом режиме зажигание дуги в фазе A (ω t= 0) происходит, когда напряжение на промежутке Uпр превысит напряжение горения дуги. Определим Uпр при погасшей дуге в фазе А по методу двух узлов:
Отсюда следует, что в прерывистом режиме начальная фаза ЗДС фазы А
равна
. Это означает, что повторное зажигание дуги в трехфазной цепи происходит
быстрее, чем в однофазной.
Для непрерывного режима начальная фаза ЭДС определяется из
выражения
Слайд 20 Приравняв выражения для ψ в
прерывистом в непрерывном режи-
мах, получим трансцендентное выражение
для связи βпр и γ для граничного режима.
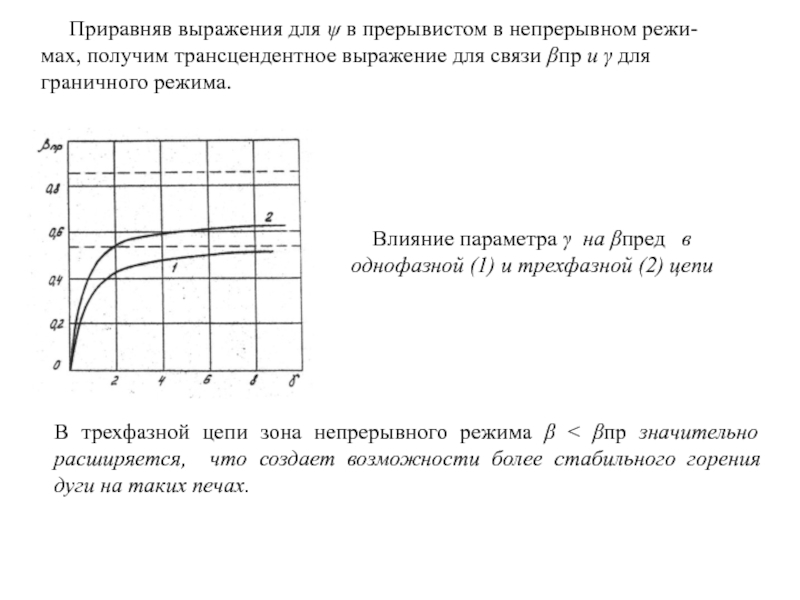
Влияние параметра γ на βпред в
однофазной (1) и трехфазной (2) цепи
В трехфазной цепи зона непрерывного режима β < βпр значительно расширяется, что создает возможности более стабильного горения дуги на таких печах.
Слайд 21Ток дуги в трехфазной цепи имеет значительно меньшую несинусоидальность, чем
в однофазной. Это связано с влиянием напряжения между нулевыми точками
источника и печи и00′. Нетрудно показать, что это напряжение содержит только гармоники, кратные трем, и равноСделаем замену переменной ν = 3 ωt. Тогда
Напряжение представляет собой напряжение прямоугольной формы с тройной частотой и амплитудой в 3 раза меньше напряжения дуги.
Как известно, расчет тока фазы трехфазной цепи может быть сведен к расчету однофазной с заменой напряжения дуга на эквивалентное напряжение
.
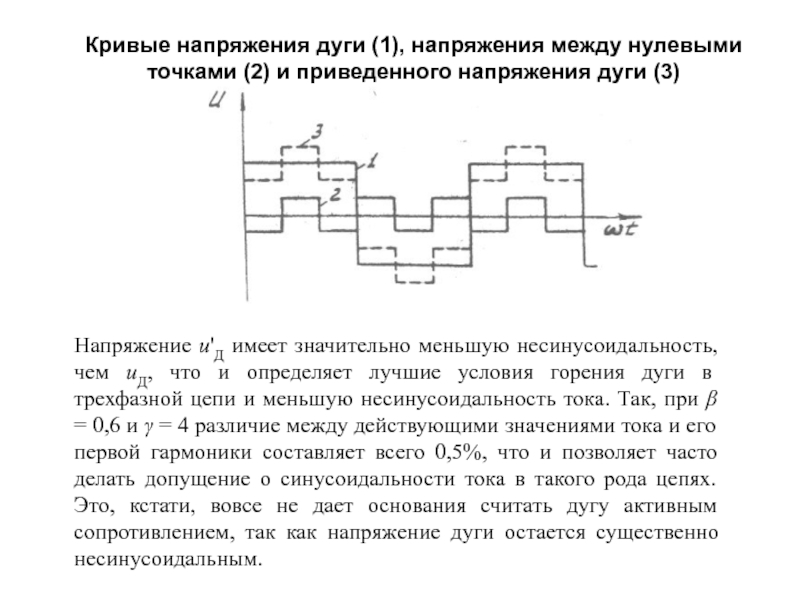
Слайд 22Кривые напряжения дуги (1), напряжения между нулевыми
точками (2) и
приведенного напряжения дуги (3)
Напряжение и'Д имеет значительно меньшую несинусоидальность, чем
иД, что и определяет лучшие условия горения дуги в трехфазной цепи и меньшую несинусоидальность тока. Так, при β = 0,6 и γ = 4 различие между действующими значениями тока и его первой гармоники составляет всего 0,5%, что и позволяет часто делать допущение о синусоидальности тока в такого рода цепях. Это, кстати, вовсе не дает основания считать дугу активным сопротивлением, так как напряжение дуги остается существенно несинусоидальным.Слайд 23
Определим мощность дуговой печи. Полная мощность, потребляемая из сети,
S = 3EфI.
Активная мощность печи потребляется из сети только на первой гармонике и составляет
Pa = 3EфI1 cos ϕ1,
где Еф, I, I 1 - действующие значения ЭДС источника, тока в его первой гармоники.
Коэффициент мощности печи
.
Определим мощность дуги
Сумма мощностей гармоник является алгебраической. Анализ показывает, что мощность дуги на высших гармониках отрицательна. Это значит, что дуга как нелинейный элемент генерирует высшие гармоники и передает их в сеть, а мощность, потребляемая в дуге, при этом снижается.
.
Слайд 24.
Тогда можно определить электрический КПД печи
.
Учитывая, что действующие значения пятой
и седьмой гармоник тока составляют примерно 8-9 и 4-5% соответственно,
в cos φ5 и сos φ7 значительно меньше cos φ1 можно считать, чтоСлайд 25Влияние инерционности дуги на процессы
в электрических цепях печей
Для анализа однофазной цепи используем уравнение Майра. Предположим,
что ток в цепи слабо отличается от синусоидаль-ного и действующее значение напряжения дуги не зависит от тока, что достаточно близко к действительности.После преобразований можно получить
Решение этого уравнения для синусоидального тока будет иметь вид
Для однофазной дуги условия перехода от непрерывного к прерывистому
режиму
Слайд 26Влияние инерционности дуги на βпред
Влияние инерционности душ на кривые
напряжения
дуги: 1- θ = 100; 2- 400 мкс
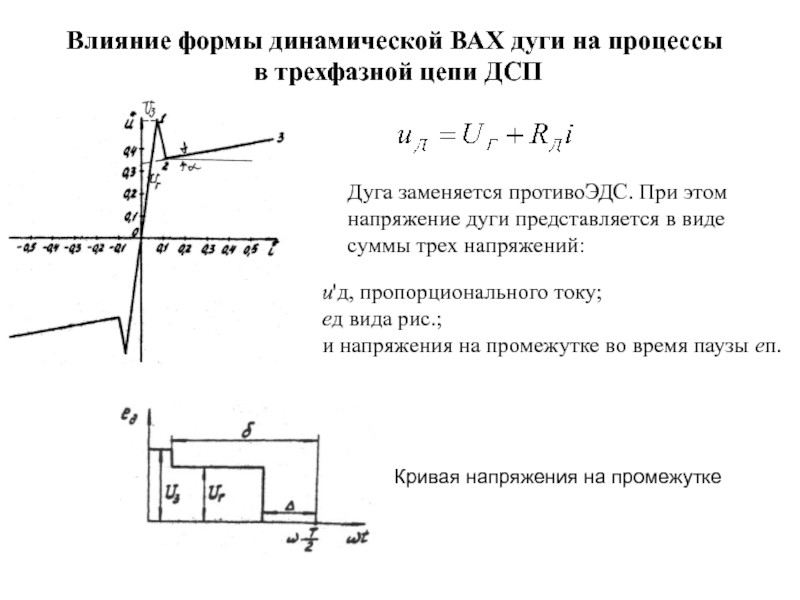
Слайд 27Влияние формы динамической ВАХ дуги на процессы
в трехфазной цепи
ДСП
Дуга заменяется противоЭДС. При этом
напряжение дуги представляется в виде
суммы трех напряжений:
и'д, пропорционального току;
ед вида рис.;
и напряжения на промежутке во время паузы еп.
Кривая напряжения на промежутке
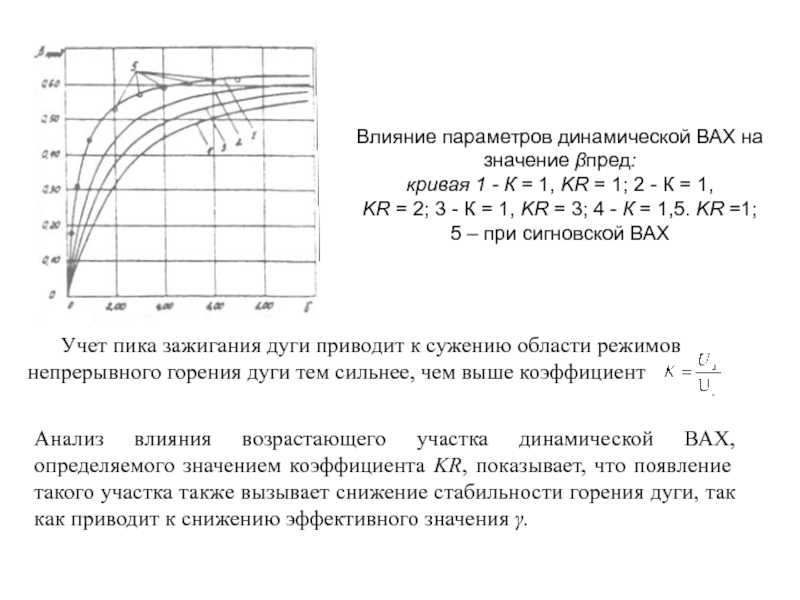
Слайд 29Влияние параметров динамической ВАХ на значение βпред:
кривая 1 -
К = 1, KR = 1; 2 - К =
1,KR = 2; 3 - К = 1, KR = 3; 4 - К = 1,5. KR =1; 5 – при сигновской ВАХ
Учет пика зажигания дуги приводит к сужению области режимов непрерывного горения дуги тем сильнее, чем выше коэффициент
Анализ влияния возрастающего участка динамической ВАХ, определяемого значением коэффициента KR, показывает, что появление такого участка также вызывает снижение стабильности горения дуги, так как приводит к снижению эффективного значения γ.