Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок повторения№1 по теме: Производная и её геометрический смысл. Производная в
Содержание
- 1. Урок повторения№1 по теме: Производная и её геометрический смысл. Производная в
- 2. Нахождение значения производной в точке(геометрический смысл производной)Нахождение
- 3. Геометрический смысл производнойПроизводная в точке
- 4. На рисунке изображён график функции
- 5. На рисунке изображён график функции
- 6. На рисунке изображены график функции у =f(x)
- 7. На рисунке изображены график функции у =f(x)
- 8. На рисунке изображены график функции у =f(x)
- 9. На рисунке изображен график функии. Найдите количество
- 10. -9 -8 -7 -6 -5 -
- 11. №9.Найдите промежутки возрастания функции .В ответе
- 12. На рисунке изображен график y=f’(x) — производной
- 13. Найдите абсциссу точки, в которой касательная к
- 14. На рисунке изображен график производной функции. Найдите
- 15. y = f /(x) 1 2
- 16. y = f /(x) 4321-1-2-3-4-5yx+––++Найдите точку экстремума функции
- 17. y = f /(x) 4321-1-2-3-4-5yx+––++Найдите количество точек экстремума
- 18. На рисунке изображен график производной функции. Найдите
- 19. На рисунке изображен график y=f'(x) — производной
- 20. На рисунке изображен график y=f‘(x) — производной
- 21. На рисунке изображен график y=f'(x) — производной
- 22. На рисунке изображен график y=f'(x) — производной
- 23. На рисунке изображен график y=f '(x) —
- 24. На рисунке изображены график функции y=f(x)
- 25. На рисунке изображен график функции y=f(x) ,
- 26. Прямая
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Нахождение значения производной в точке(геометрический смысл производной)
Нахождение промежутков возрастания и
убывания
Нахождение точек, в которых производная равна 0
Нахождение наибольшего и наименьшего
значения функцииТипы задач из ЕГЭ по математике:
Слайд 3 Геометрический смысл производной
Производная в точке
равна
угловому коэффициенту
касательной кграфику функции
y = f(x) в этой точке.
Т.е.
Причем, если :
.
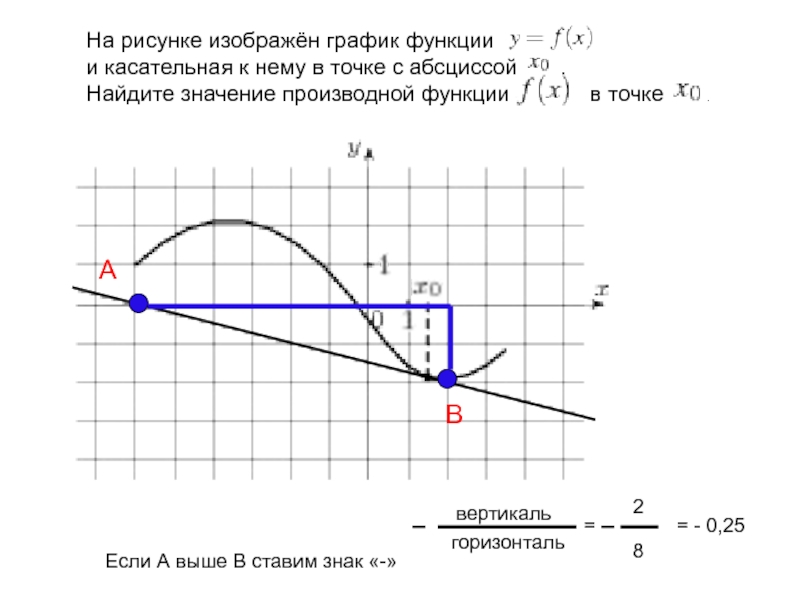
Слайд 4На рисунке изображён график функции
и касательная к
нему в точке с абсциссой .
Найдите значение производной
функции в точке .А
В
Если А выше В ставим знак «-»
вертикаль
горизонталь
=
2
8
= - 0,25
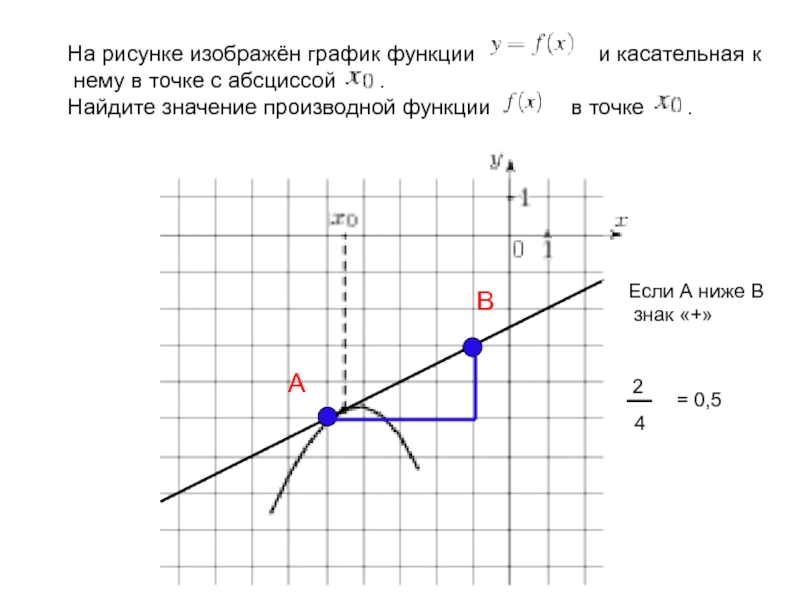
Слайд 5На рисунке изображён график функции и касательная к
нему в точке с абсциссой .
Найдите значение производной
функции в точке .А
В
Если А ниже В
знак «+»
2
4
= 0,5
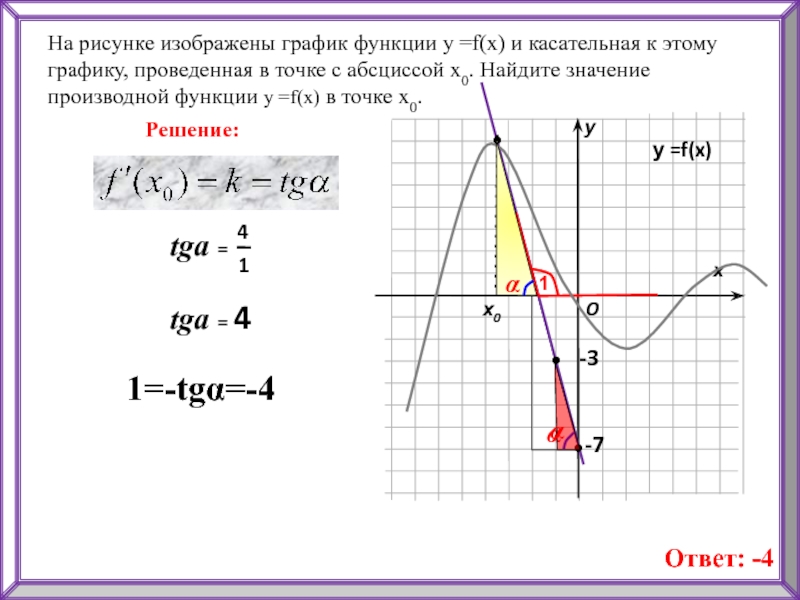
Слайд 6На рисунке изображены график функции у =f(x) и касательная к
этому графику, проведенная в точке с абсциссой х0. Найдите значение
производной функции у =f(x) в точке х0.х
х0
у
Решение:
O
у =f(x)
-3
-7
1=-tgα=-4
Ответ: -4
Слайд 7На рисунке изображены график функции у =f(x) и касательная к
этому графику, проведенная в точке с абсциссой х0. Найдите значение
производной функции у =f(x) в точке х0.х
х0
у
Решение:
O
у =f(x)
1
a
Ответ: 0,25
Слайд 8На рисунке изображены график функции у =f(x) и касательная к
этому графику, проведенная в точке с абсциссой х0. Найдите значение
производной функции у =f(x) в точке х0.х
х0
у
Решение:
O
у =f(x)
1
a
a
Ответ: -0,25
tga =0,25
1=-tg α=-0,25
Слайд 9На рисунке изображен график функии. Найдите количество точек, в которых
производная функции равна 0.
Производная функции в точке равна 0 тогда
и только тогда, когда касательная к графику функции, проведенная в этой точке, горизонтальна.Слайд 10 -9 -8 -7 -6 -5 - 4 -3 -2
-1
1 2 3 4 5 6
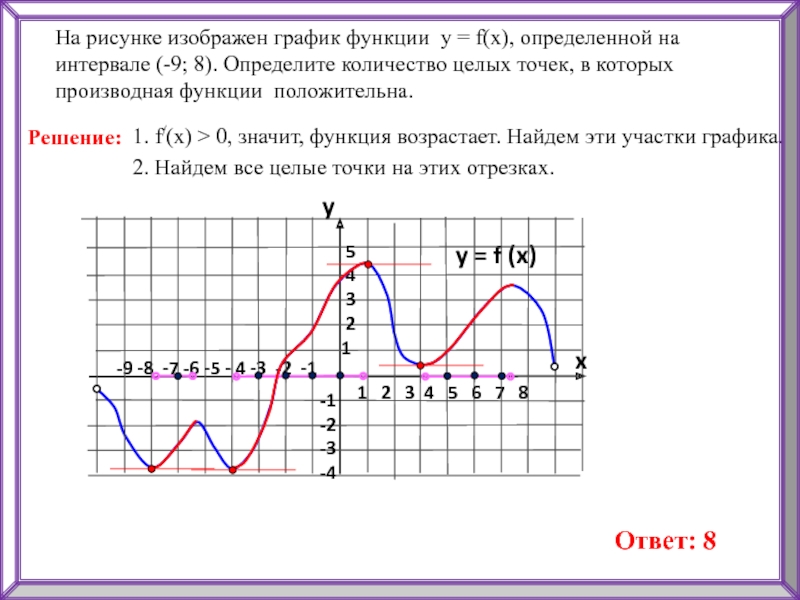
7 8На рисунке изображен график функции у = f(x), определенной на интервале (-9; 8). Определите количество целых точек, в которых производная функции положительна.
y = f (x)
y
x
5
4
3
2
1
-1
-2
-3
-4
1. f/(x) > 0, значит, функция возрастает. Найдем эти участки графика.
2. Найдем все целые точки на этих отрезках.
Ответ: 8
Решение:
Слайд 11№9.Найдите промежутки возрастания функции .В ответе укажите длину большего
из них.
На рисунке изображен график производной функции. Найдите количество таких
чисел , что касательная у графику в точке параллельна прямой y=3x-11 или совпадает с ней.Две прямые параллельны или совпадают, тогда и только тогда, когда угловые коэффициенты равны.
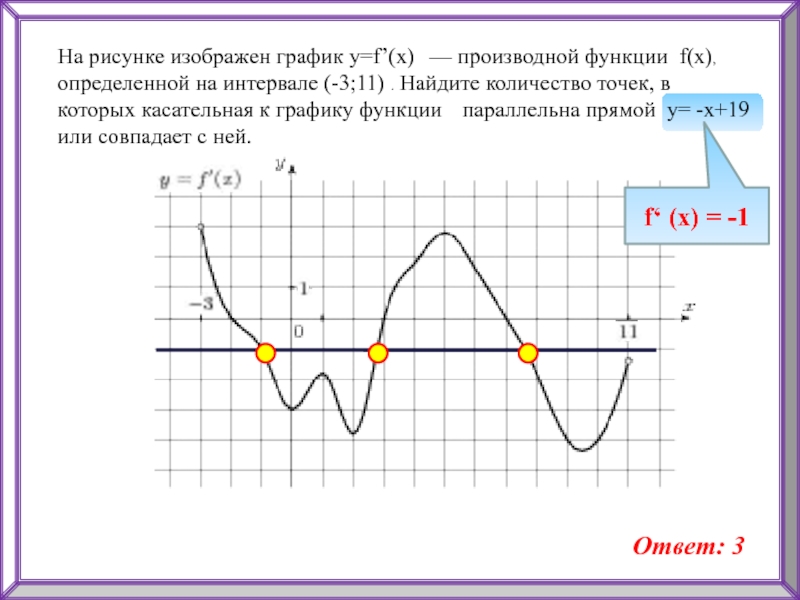
Слайд 12На рисунке изображен график y=f’(x) — производной функции f(x), определенной
на интервале (-3;11) . Найдите количество точек, в которых касательная
к графику функции параллельна прямой y= -x+19 или совпадает с ней.f‘ (x) = -1
Ответ: 3
Слайд 13Найдите абсциссу точки, в которой касательная к графику функции
параллельна прямой y=2x+7 или совпадает с ней.
Две прямые параллельны
или совпадают, тогда и только тогда, когда угловые коэффициенты равны.Слайд 14На рисунке изображен график производной функции. Найдите промежутки убывания функции.
В ответе укажите сумму целых чисел, входящих в эти промежутки.
Производная
непрерывно дифференцируемой функции на промежутке убывания (возрастания) отрицательна (положительна)-1+0+1+2+3+4+7=16
Слайд 15y = f /(x)
1 2 3 4
5 6 7
-7 -6 -5 -4 -3 -2
-14
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
На рисунке изображен график производной функции. Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек минимума.
4 точки экстремума
Ответ:2
-8
8
Слайд 16y = f /(x)
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
Найдите точку экстремума функции у =f (x)
на отрезке [– 6; –1]
Ответ:– 5
1 2 3
4 5 6 7-7 -6 -5 -4 -3 -2 -1
-8
8
Слайд 17y = f /(x)
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
Найдите количество точек экстремума функции у =f
(x)
на отрезке [– 3; 7]
Ответ: 3
1 2
3 4 5 6 7-7 -6 -5 -4 -3 -2 -1
-8
8
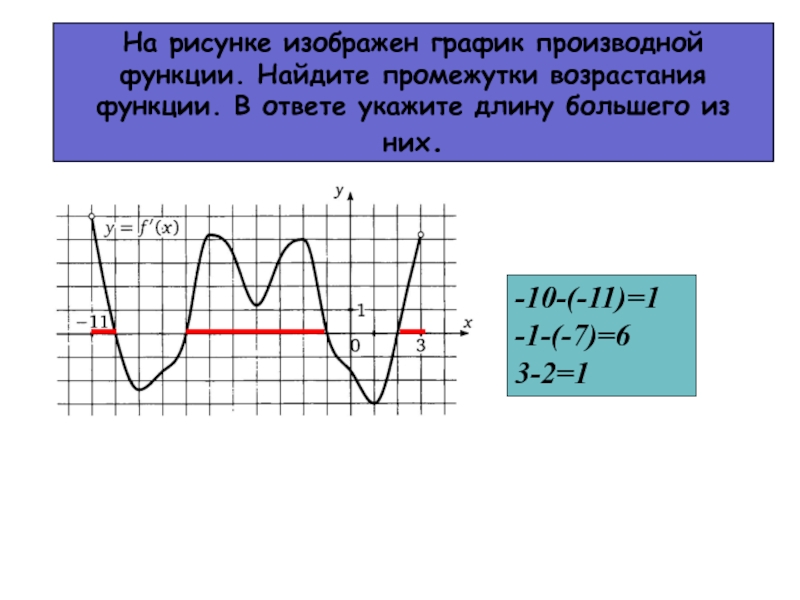
Слайд 18На рисунке изображен график производной функции. Найдите промежутки возрастания функции.
В ответе укажите длину большего из них.
-10-(-11)=1
-1-(-7)=6
3-2=1
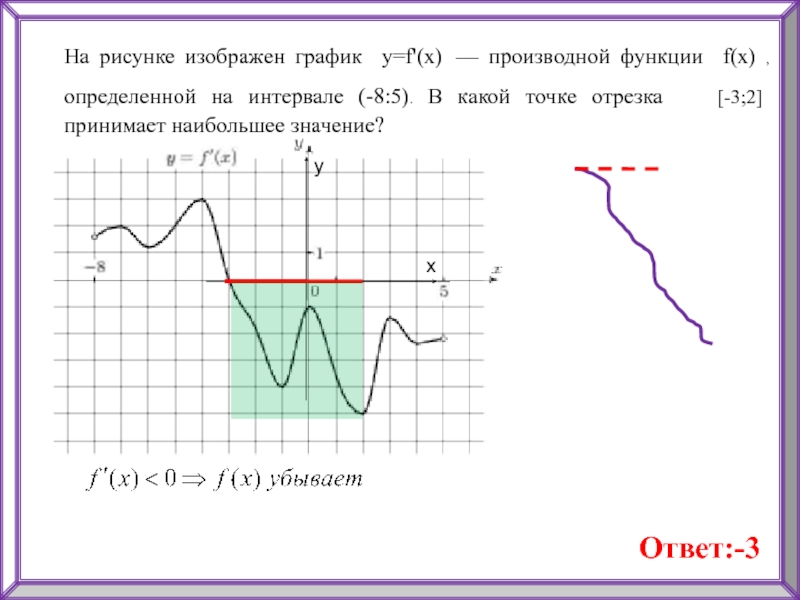
Слайд 19На рисунке изображен график y=f'(x) — производной функции f(x) ,
определенной на интервале (-8:5). В какой точке отрезка [-3;2]
принимает наибольшее значение?Ответ:-3
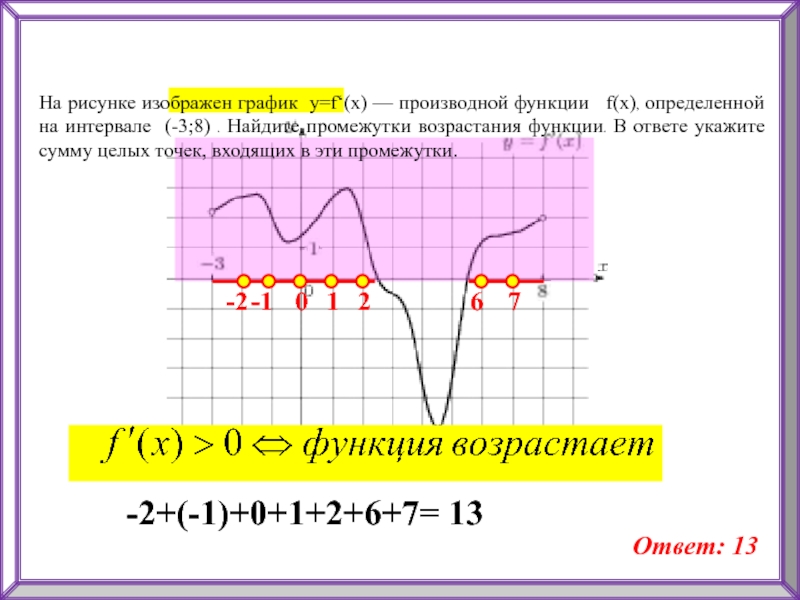
Слайд 20На рисунке изображен график y=f‘(x) — производной функции f(x),
определенной на интервале (-3;8) . Найдите промежутки возрастания функции. В
ответе укажите сумму целых точек, входящих в эти промежутки.-2
-1
0
1
2
6
7
-2+(-1)+0+1+2+6+7= 13
Ответ: 13
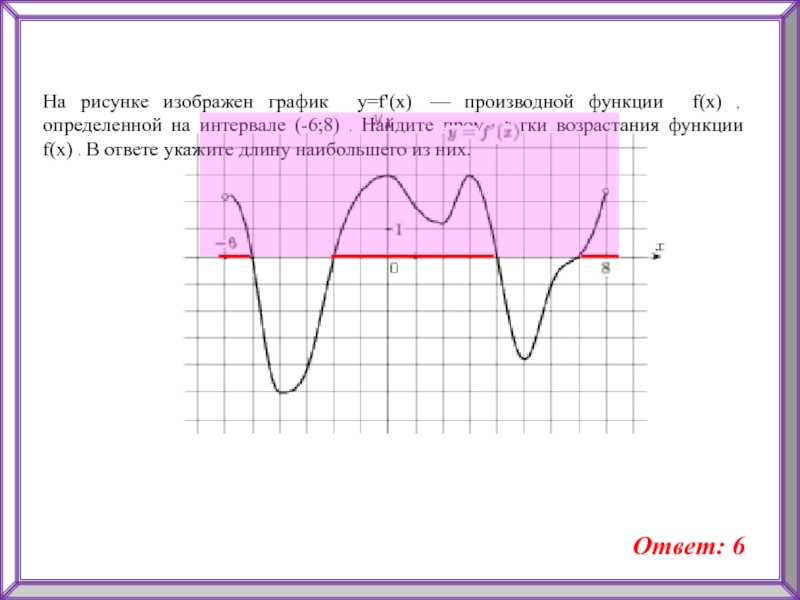
Слайд 21На рисунке изображен график y=f'(x) — производной функции f(x) ,
определенной на интервале (-6;8) . Найдите промежутки возрастания функции f(x)
. В ответе укажите длину наибольшего из них.Ответ: 6
Слайд 22На рисунке изображен график y=f'(x) — производной функции f(x),
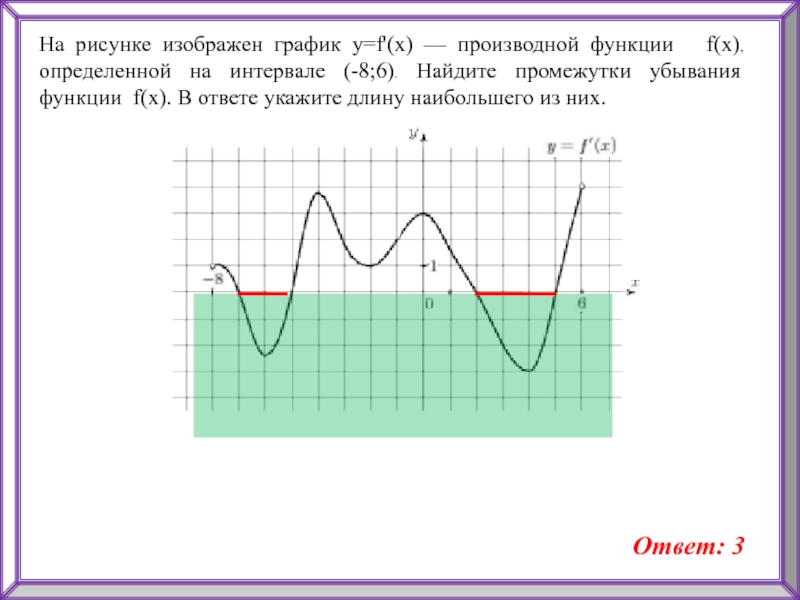
определенной на интервале (-8;6). Найдите промежутки убывания функции f(x). В
ответе укажите длину наибольшего из них.Ответ: 3
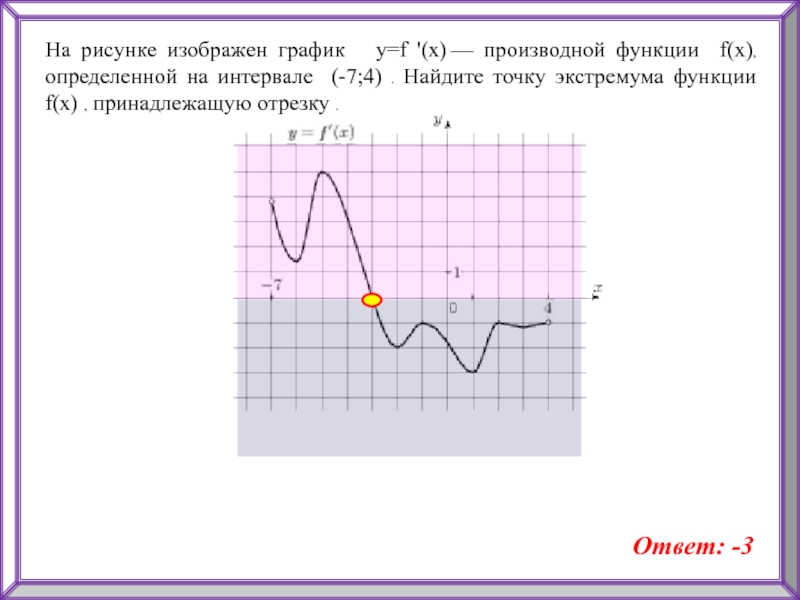
Слайд 23На рисунке изображен график y=f '(x) — производной функции f(x),
определенной на интервале (-7;4) . Найдите точку экстремума функции f(x)
, принадлежащую отрезку .Ответ: -3
Слайд 24На рисунке изображены график функции y=f(x) и касательная к
нему в точке с абсциссой x0 . Найдите значение производной
функции f(x) в точке x0 .Слайд 25На рисунке изображен график функции y=f(x) , определенной на интервале
. Найдите количество точек, в которых производная функции
равна 0 .Слайд 26 Прямая параллельна
касательной к графику функции
. Найдите абсциссу точки касания.Две прямые параллельны или совпадают, тогда и только тогда, когда угловые коэффициенты равны.









![Урок повторения№1 по теме: Производная и её геометрический смысл. Производная в y = f /(x) 4321-1-2-3-4-5yx+––++Найдите точку экстремума функции у =f (x) на y = f /(x) 4321-1-2-3-4-5yx+––++Найдите точку экстремума функции у =f (x) на отрезке [– 6; –1]Ответ:– 51](/img/thumbs/c804b0cbfeb8418fdcffce0591837099-800x.jpg)
![Урок повторения№1 по теме: Производная и её геометрический смысл. Производная в y = f /(x) 4321-1-2-3-4-5yx+––++Найдите количество точек экстремума функции у =f (x) y = f /(x) 4321-1-2-3-4-5yx+––++Найдите количество точек экстремума функции у =f (x) на отрезке [– 3; 7]Ответ: 31](/img/thumbs/566596e8663b9ddfc040ccb3ce348022-800x.jpg)