Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Условия Гаусса-Маркова
Содержание
- 1. Условия Гаусса-Маркова
- 2. Условия Гаусса-Маркова1. На самом деле это требование несущественно, если в модель включена константа
- 3. Условия Гаусса-Маркова2. условие гомоскедастичности (постоянства дисперсии)
- 4. Условия Гаусса-МарковаИллюстрация гомоскедастичности
- 5. Условия Гаусса-МарковаИллюстрация гетероскедастичности
- 6. Условия Гаусса-Маркова3. автокорреляция отсутствует
- 7. Условия Гаусса-Марковаавтокорреляции отсутствуетавтокорреляции присутствует
- 8. Если выполнены все 3 условия, то модель
- 9. Если к 3-м условиям добавляют четвертое 4)
- 10. Предположение о нормальности основано на центральной предельной теореме.Условия Гаусса-Марковаплотность вероятности0
- 11. ТЕОРЕМА ГАУССА-МАРКОВАВ КЛАССИЧЕСКОЙ ЛИНЕЙНОЙ МОДЕЛИ ПАРНОЙ РЕГРЕССИИ
- 12. Оценки тем точнее, чем разнообразнее выборка по
- 13. Скачать презентанцию
Условия Гаусса-Маркова1. На самом деле это требование несущественно, если в модель включена константа
Слайды и текст этой презентации
Слайд 2Условия Гаусса-Маркова
1.
На самом деле это требование несущественно, если в
модель включена константа
Слайд 8
Если выполнены все 3 условия, то модель
парной регрессии
Условия Гаусса-Маркова
Слайд 9
Если к 3-м условиям добавляют четвертое
4) Нормальность ошибок:
То модель называется
классической нормальной линейной моделью
парной регрессии
Условия Гаусса-Маркова
Слайд 10
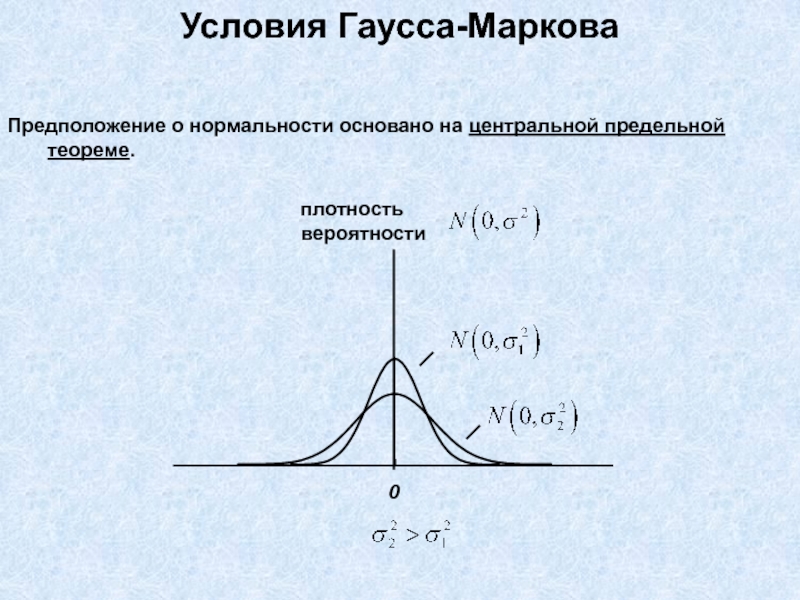
Предположение о нормальности основано на центральной предельной теореме.
Условия Гаусса-Маркова
плотность вероятности
0
Слайд 11ТЕОРЕМА ГАУССА-МАРКОВА
В КЛАССИЧЕСКОЙ ЛИНЕЙНОЙ МОДЕЛИ ПАРНОЙ РЕГРЕССИИ (выполнены 3 условия
Гаусса-Маркова) ОЦЕНКИ НАИМЕНЬШИХ КВАДРАТОВ
ЯВЛЯЮТСЯ НАИЛУЧШИМИ (имеют наибольшую точность).
Если модель является
нормальной (выполнены 4 условий Гаусса-Маркова), то ОНК имеют нормальное распределение Нормальность позволяет проверять гипотезы и строить доверительные
интервалы для прогноза.
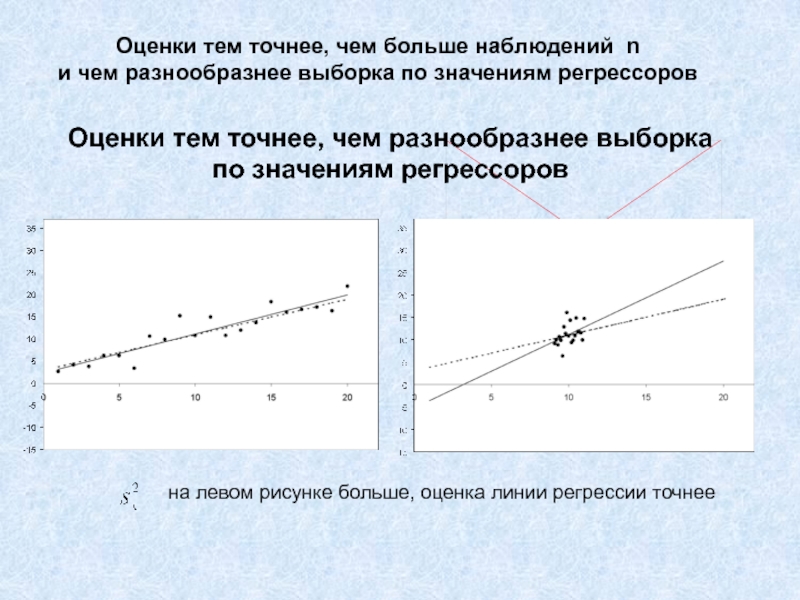
Слайд 12Оценки тем точнее, чем разнообразнее выборка по значениям регрессоров
на левом
рисунке больше, оценка линии регрессии точнее
Оценки тем точнее, чем больше
наблюдений nи чем разнообразнее выборка по значениям регрессоров