Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выбор факторов модели
Содержание
- 1. Выбор факторов модели
- 2. Основные определенияЭксперимент - это система операций, воздействий и
- 3. Планирование эксперимента — это процедура выбора числа
- 4. Слайд 4
- 5. Эксперимент используется для
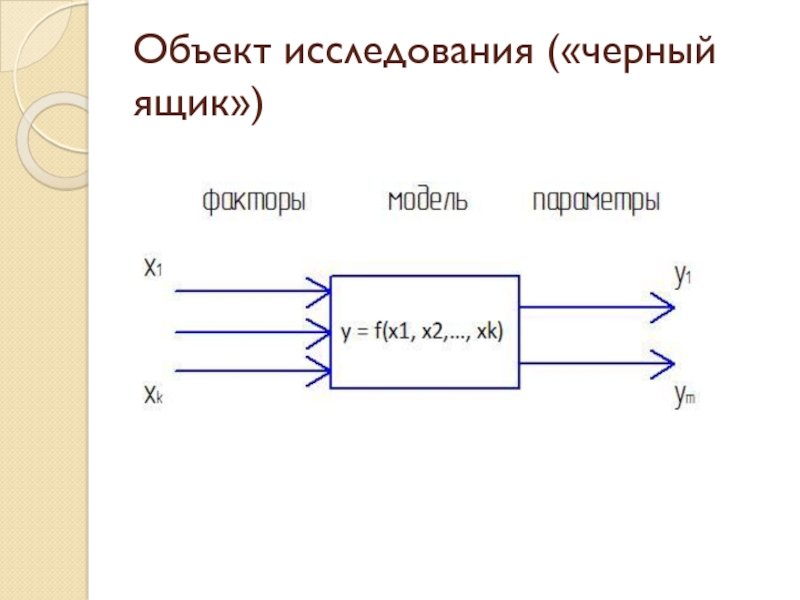
- 6. Объект исследования («черный ящик»)
- 7. Пример Объект – автобусПараметр – t0 время
- 8. Математическая модель – это уравнение, связывающее параметр
- 9. Одно из возможных состояний «черного ящика» образуется
- 10. Чтобы узнать число различных состояний, достаточно число
- 11. ФакторыФактор – это измеряемая переменная величина, принимающая
- 12. Область определения может быть непрерывной и дискретной.
- 13. Слайд 13
- 14. Требования к факторам при планировании экспериментаУправляемость –
- 15. Требования к совокупности факторовСовместимость – комбинации факторов
- 16. Подходы к отбору факторов
- 17. Множественная регрессияДля отбора факторов при построении модели
- 18. Требования к включаемым факторам1. Они должны быть
- 19. Отбор факторов обычно осуществляется в две стадии:–
- 20. 1. Проверка парной корреляцииКоэффициенты интеркорреляции (т. е.
- 21. 2. Оценка мультиколлинеарности факторов. При наличии мультиколлинеарности
- 22. 3. Использование частных коэффициентов корреляции при отсеве
- 23. Пример: Представлена информация об объемах продаж и
- 24. Матрица коэффициентов парной корреляциикоэффициент частной корреляции, характеризующий
- 25. ryx1x2 x3 =-
- 26. Скачать презентанцию
Основные определенияЭксперимент - это система операций, воздействий и (или) наблюдений, направленных на получение информации об объекте при исследовательских испытанияхОпыт – это воспроизведение исследуемого явления в определенных условиях проведения эксперимента при возможности регистрации
Слайды и текст этой презентации
Слайд 1Выбор факторов модели
Выполнил: студент гр. АП-501 Снигур А.С.
Проверил: проф. Чигиринская
Н.В.
Слайд 2Основные определения
Эксперимент - это система операций, воздействий и (или) наблюдений, направленных
на получение информации об объекте при исследовательских испытаниях
Опыт – это
воспроизведение исследуемого явления в определенных условиях проведения эксперимента при возможности регистрации его результатовПлан эксперимента – это совокупность данных, определяющих число, условия и порядок реализации опытов
Слайд 3Планирование эксперимента — это процедура выбора числа и условий проведения
опытов, необходимых и достаточных для решения поставленной задачи с требуемой
точностью. При этом существенно следующее:- стремление к минимизации общего числа опытов;
- одновременное варьирование всеми переменными, определяющими процесс, по специальным правилам — алгоритмам;
- использование математического аппарата, формализующего многие действия экспериментатора;
- выбор четкой стратегии, позволяющей принимать обоснованные решения после каждой серии экспериментов.
Слайд 5 Эксперимент используется для следующих задач: поиск
оптимальных условий (экстремальные задачи, связанные с поиском экстремума), построение интерполяционных
формул, выбор существенных факторов, оценка и уточнение констант теоретических моделей (например, кинетических), выбор наиболее приемлемых из некоторого множества гипотез о механизме явлений.Слайд 7Пример
Объект – автобус
Параметр – t0 время оборота автобуса на
маршруте
Факторы - lм – длина маршрута;
VТ – техническая скорость;
n –
число промежуточных остановок на маршруте;tос – время простоя на промежуточной остановке;
tк – время простоя на конечных остановках.
Модель -
Слайд 8Математическая модель – это уравнение, связывающее параметр оптимизации с факторами.
В общем виде его можно записать так:
y = f(x1, x2,…,
xk)Такая функция называется функцией отклика.
Уровень – значение фактора, которое он может принимать в опыте.
Фактор может принимать как бесконечно многое число значений (непрерывный ряд), так и иметь определенное число дискретных уровней.
Слайд 9Одно из возможных состояний «черного ящика» образуется фиксированным набором уровней
факторов (т. е. установление каждого фактора на некоторый уровень), который
также составляет условия проведения одного из возможных опытов.Все возможные наборы состояний «черного ящика» составляют число возможных различных опытов – и характеризуют сложность системы.
Слайд 10Чтобы узнать число различных состояний, достаточно число уровней факторов (если
оно для всех факторов одинаково) возвести в степень числа факторов
k:pk, где p – число уровней.
Требования к объекту исследования:
- воспроизводимость (характеризуется разбросом параметров в различных опытах при одинаковом наборе факторов);
- управляемость (возможность выбора уровней факторов в активном и активно-пассивном эксперименте).
Слайд 11Факторы
Фактор – это измеряемая переменная величина, принимающая в некоторый момент
времени определенное значение. Факторы соответствуют способам воздействия на объект исследования.
Фактор
считается заданным, если вместе с его названием указана область его определения. Слайд 12Область определения может быть непрерывной и дискретной. Но в решении
задач для факторов с непрерывной областью определения, таких, как температура,
время, количество вещества и т. п., всегда выбираются дискретные множества уровней.В практических задачах области определения факторов, как правило, ограничены. Ограничения могут носить принципиальный либо технический характер.
Слайд 14Требования к факторам при планировании эксперимента
Управляемость – возможность выбора уровней
фактора и поддержания их в одном состоянии на протяжении всего
экспериментаОперациональность – выбор размерности фактора и точность его фиксирования
Точность замера (степень точности определяется диапазоном изменения факторов)
Однозначность – непосредственное воздействие на объект, фактор не является функцией других факторов
Слайд 15Требования к совокупности факторов
Совместимость – комбинации факторов осуществимы и безопасны.
Несовместимость может наблюдаться на границах или внутри областей определения факторов.
Решение – сокращение области или разбиение на подобластиНезависимость (некоррелируемость) – возможность установления фактора на любом уровне вне зависимости от уровня других факторов (отсутствие линейной зависимости между факторами)
Слайд 17Множественная регрессия
Для отбора факторов при построении модели используется множественная регрессия.
С ее помощью можно определить влияние каждого из факторов в
отдельности, а также их совокупное воздействие на моделируемый показатель.Основные типы функций, используемые при количественной оценке связей:
линейная функция: у = а0 + a1х1 + а2х2,+ ... + amxm. Параметры a1, а2, am, называются коэффициентами «чистой» регрессии и характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне;
нелинейные функции: у=ах1b1 х2b2....xmbm- - степенная функция; b1, b2..... bm - коэффициенты эластичности; показывают, насколько % изменится в среднем результат при изменении соответствующего фактора на 1 % и при неизменности действия других факторов.
Слайд 18Требования к включаемым факторам
1. Они должны быть количественно измеримы. Если
необходимо включить в модель качественный фактор, не имеющий количественного измерения,
то ему нужно придать количественную определенность.2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи. Включение в модель факторов с высокой интеркорреляцией может привести к нежелательным последствиям - система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.
3. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми.
Слайд 19Отбор факторов обычно осуществляется в две стадии:
– на первой подбираются
факторы исходя из сущности проблемы;
– на второй – на основе
матрицы показателей корреляции определяютt-статистики для параметров регрессии.
Слайд 201. Проверка парной корреляции
Коэффициенты интеркорреляции (т. е. корреляции между объясняющими
переменными) позволяют исключать из модели дублирующие факторы. Считается, что две
переменные явно коллинеарные, т. е. находятся между собой в линейной зависимости, если rxi,xj 0,7Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.
Слайд 212. Оценка мультиколлинеарности факторов.
При наличии мультиколлинеарности факторов, т.е. когда более
чем два фактора связаны между собой линейной зависимостью, имеет место
совокупное воздействие факторов друг на друга.Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
Слайд 223. Использование частных коэффициентов корреляции при отсеве фактора.
Частные коэффициенты (индексы)
корреляции характеризуют тесноту связи между результатом и соответствующим фактором при
устранении влияния других факторов, включенных в уравнение регрессии.0,1- 0,3- слабая связь
0,3-0,5 – умеренная связь
0,5-0,7- заметная связь
0,7-0,9- тесная связь
0,9-0,99- весьма тесная
Слайд 23Пример: Представлена информация об объемах продаж и затратах на рекламу
одной фирмы, а также индекс потребительских расходов и средняя заработная
плата за ряд текущих лет.х1 - затраты на рекламу, тыс. руб.
х2 - индекс потребительских расходов, %
х3 - средняя заработная плата, тыс. руб.
у- объем продаж, тыс. руб.
Дана матрица межфакторной корреляции:
R= , Det |R|= 0,29659
Det |R| ≠ 0, мультиколлинеарность отсутствует.
Слайд 24Матрица коэффициентов парной корреляции
коэффициент частной корреляции, характеризующий степень тесноты связи
между результатом (y) и первым фактором (х1) при неизменном значении
оставшихся двух факторов, определим по формуле:ryx1x2 x3 =
где Ryx1 = (-1)1+2 = - 0,1492626
Ryy= (-1) 1+1 = 0,29659,
Rx1x1= (-1)2+2 = 0,117981
Слайд 25ryx1x2 x3 =-
=-
= 0,79988Аналогично находим еще два коэффициента частной корреляции
ryx2x1 x3 = 0,68639
ryx3x1 x2 =0,11154
На основе значений коэффициентов частной корреляции можно сделать вывод, что наибольшее влияние на результат при неизменном уровне остальных факторов оказывает первый фактор, т.е. затраты на рекламу.