Механический и геометрический смысл производной

математики. Оно возникло в XVII в. в связи с необходимостью

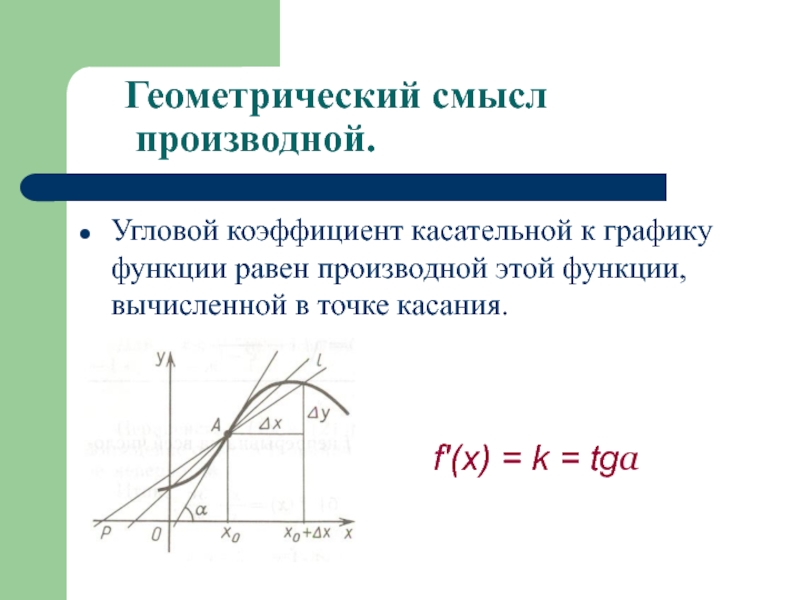
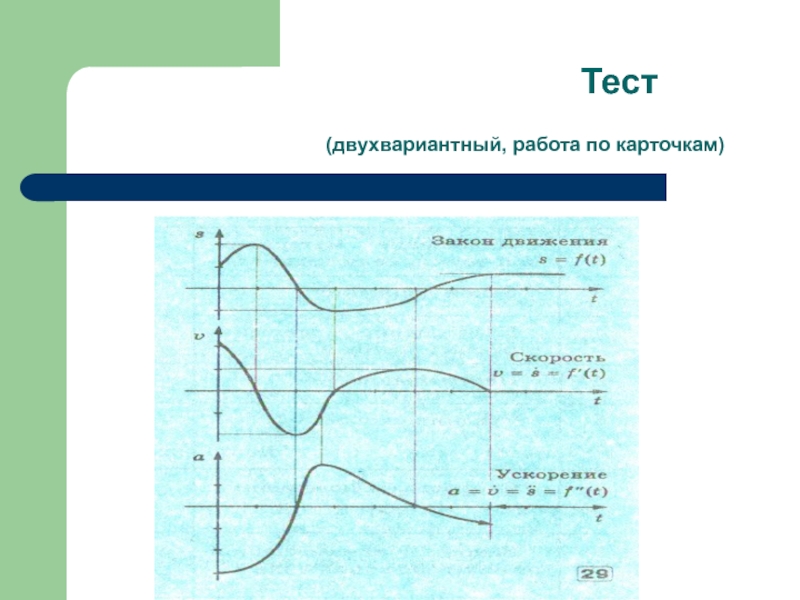
решения ряда задач из физики, механики и математики, но в первую очередь для определения скорости прямолинейного движения и построения касательной к кривой.
Независимо друг от друга И.Ньютон и Г. Лейбниц разработали аппарат исчисления, которым мы пользуемся в настоящее время. Ньютон исходил в основном из задач механики (опирался на физическое представление о мгновенной скорости движения, считая его очевидным и, сводя к нему другие случаи производной), а Лейбниц по преимуществу исходил из геометрических задач (использовал понятие бесконечно малой).
Исчисление, созданное Ньютоном и Лейбницем, получило название дифференциального исчисления.

Готфрид Фридрих
(1646 – 1716) – великий немецкий учёный. Философ, математик,

физик, юрист, языковед.

ВЕЛИКИЕ УЧЁНЫЕ

закону S=f(t).
Скорость прямолинейного движения материальной точки в любой момент

времени t есть производная от пути S по времени t:


Ускорение прямолинейного движения материальной точки в любой момент времени t есть производная от скорости υ по времени t:

выражает скорость протекания процесса, описываемого зависимостью y = f(x).
Это может означать, например, следующее:  Если

нас интересует движение автомобиля, то, принимая в качестве функции зависимость пройденного расстояния от времени, с помощью производной мы получим зависимость скорости от времени.  Если же мы рассматриваем в качестве функции мгновенную скорость автомобиля, то производная задает изменение его ускорения.  Если мы рассматриваем функцию, задающую зависимость объема произведенной продукции от времени, то производная позволит узнать, как изменялась со временем производительность труда на этом предприятии. Если мы рассматриваем электромагнитные волны, то нам могут потребоваться функции, характеризующие изменение со временем электрического и магнитного полей, а также их производные - скорости изменения этих полей, ведь величина магнитного поля пропорциональна скорости изменения электрического поля. И т.п.
Решая конкретные текстовые задачи на скорость процесса с применением производной, следует не забывать о размерностях величин. Если переменная y, заданная функцией f(x) измеряется в некоторых единицах [y], а её аргумент в единицах [x], то производная (скорость) измеряется в единицах [y/x].

касательной к графику функции равен производной этой функции, вычисленной в

точке касания.

f′(x) = k = tga

вопрос школьники и даже студенты пытаются ответить: "Прямая, имеющая одну

общую точку с графиком функции." Это не так. Одну общую точку касательная и график функции, как правило, имеют только в локальной окрестности этой точки, за пределами такой окрестности могут быть разные варианты "взаимодействия" прямой и графика. И даже из этого правила существуют исключения. Например, задумайтесь о том, что такое касательные к графику линейной функции? Сколько общих точек с графиком функции у = sinx имеет прямая y = 1?

ВАЖНО !!!

Касательная - это предельное положение секущей.

на расстоянии
S=t³+2t²+3t км от станции отправления.
Найти:
а) выражение для

ускорения через t часов после начала движения;
б) ускорение через 2 часа после начала движения?

к графику функции Y=4/x, с осью Ох в точке

с абсциссой
хₒ= - 2.

1) 45º ; 2) 30º ; 3) 60º ; 4) 135º

Дифференциал в физике. Рассматривается связь между тремя величинами, получаются равенства

dy = k dx, где k – это производная y по x ( k – коэффициент пропорциональности между бесконечно малыми изменениями взаимосвязанных величин)

Сила – производная работы по перемещению.


Сила тока – производная заряда по времени.


Линейная плотность – производная массы (тонкого стержня) по длине.


Теплоёмкость – производная теплоты по температуре.


Мощность – производная работы по времени.

по закону

а) выведите формулу для вычисления скорости движения

точки в любой момент времени t ( t > 0);
б) найдите скорость в в момент t = 2c;
в) через сколько секунд после начала
движения точка остановится?


И ещё две задачи: № 268.
Материальная точка движется прямолинейно по закону
x(t) = t 3 – 4 t 2 .Перемещение измеряется в метрах.
Найдите:
скорость в момент t = 5c;
ускорение в момент t = 5c.

Задачи Дорогие ученики, Вам предлагаются для решения пять небольших задач, три из них в № 267, две – в № 268.

№267 (а, б, в)
а) V(t) = - t 2 + 4 t + 5.
б) V(2) = - 2 2 + 4∙2 + 5 = - 4 + 8 + 5 = 9(м/с).
в) V(t) = 0, - t 2 + 4 t + 5 = 0, t1 = -1, t2 = 5,
-1 < 0, не удовлетворяет условию задачи.
Точка остановится через 5 секунд после начала движения.
------------------------------------------------------------------------------------
№268
Решение.
V(t) = x′(t) = 3 t 2 - 8 t ; V(5) = 3 ∙ 5 2 – 8 ∙ 5 = 35 (м/с).
a(t) = x′′(t) = 6t – 8; a(5) = 6 ∙ 5 – 8 = 22 (м/с 2).

Решение задач
Самооценка: 5 заданий – «5», 4 задания – «4», 3 задания – «3», 2 задания – «2», одно – «1»

Тест (двухвариантный, работа по карточкам)

Подведём и т о г

Спасибо за работу !!!
Оценочный лист участников семинара – практикума

«Применение производной в физике и технике»