Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение производной к исследованию функций
Содержание
- 1. Применение производной к исследованию функций
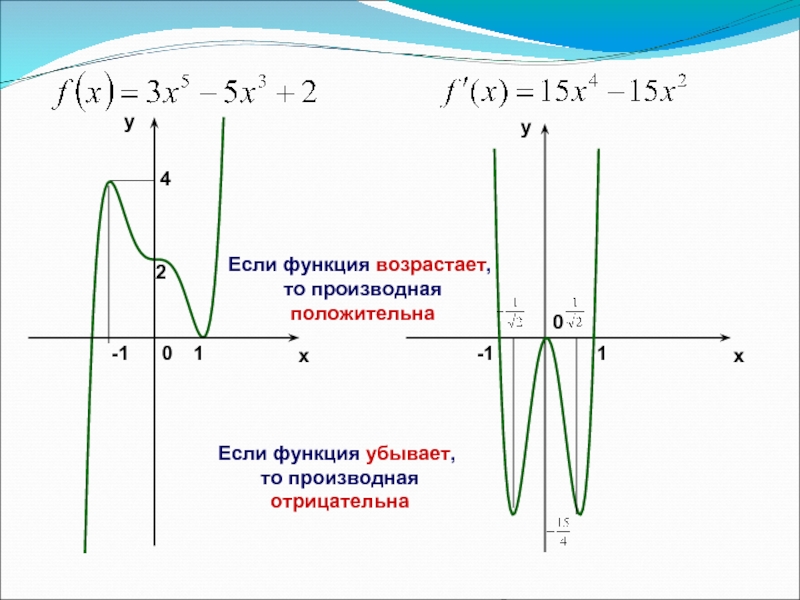
- 2. xyyx2-1140-110Если функция возрастает, то производная положительнаЕсли функция убывает, то производная отрицательна
- 3. Слайд 3
- 4. Находим производную функцииНаходим критические точки функцииЕсли критических
- 5. х = 1 ;
- 6. -9 -8 -7 -6 -5 -
- 7. -9 -8 -7 -6 -5 -
- 8. Непрерывная функция у = f(x) задана на
- 9. На рисунке изображен график производной функции у
- 10. y = f /(x) 1 2
- 11. y = f /(x) 4321-1-2-3-4-5yx+––++Найдите количество точек экстремума
- 12. На рисунке изображен график функции f(x),
- 13. На рисунке изображен график y=f'(x) — производной
- 14. На рисунке изображен график y=f'(x) — производной
- 15. На рисунке изображен график y=f'(x) — производной
- 16. На рисунке изображен график y=f'(x) — производной
- 17. Скачать презентанцию
xyyx2-1140-110Если функция возрастает, то производная положительнаЕсли функция убывает, то производная отрицательна
Слайды и текст этой презентации
Слайд 2
x
y
y
x
2
-1
1
4
0
-1
1
0
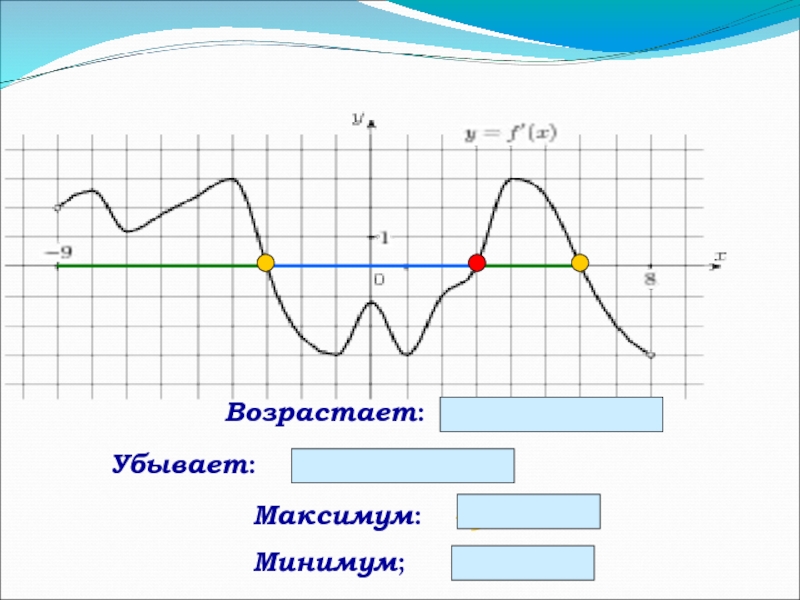
Если функция возрастает,
то производная
положительна
Если функция убывает,
то производная
отрицательна
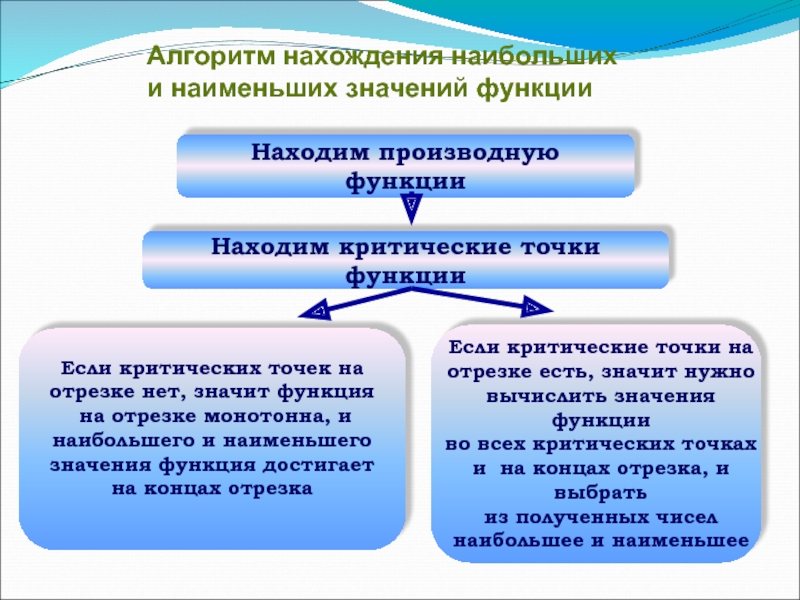
Слайд 4Находим производную функции
Находим критические точки функции
Если критических точек на
отрезке
нет, значит функция
на отрезке монотонна, и
наибольшего и наименьшего
значения функция
достигаетна концах отрезка
Если критические точки на отрезке есть, значит нужно вычислить значения функции
во всех критических точках и на концах отрезка, и выбрать
из полученных чисел
наибольшее и наименьшее
Алгоритм нахождения наибольших
и наименьших значений функции
Слайд 5
х = 1 ; х = 5/3
f(-1)=18
f(3) = 2
f(1) = 6
f(5/3) = 55/9
max f(x)=f(-1)=18
[-1;3]
min f(x)=f(3)=2
[-1;3]
ответ
Решение:
Слайд 6 -9 -8 -7 -6 -5 - 4 -3 -2
-1
1 2 3 4 5 6
7 8На рисунке изображен график функции у = f(x), определенной на интервале (-9; 8). Определите количество целых точек, в которых производная функции положительна.
y = f (x)
y
x
5
4
3
2
1
-1
-2
-3
-4
1. f/(x) > 0, значит, функция возрастает. Найдем эти участки графика.
2. Найдем все целые точки на этих отрезках.
Ответ: 8
Решение:
Слайд 7 -9 -8 -7 -6 -5 - 4 -3 -2
-1
1 2 3 4 5 6
7 8На рисунке изображен график функции у = f(x), определенной на интервале (-5; 5). Определите количество целых точек, в которых производная функции отрицательна.
y = f (x)
y
x
5
4
3
2
1
-1
-2
-3
-4
1. f/(x) < 0, значит, функция убывает. Найдем эти участки графика.
2. Найдем все целые точки на этих отрезках.
Ответ: 5
Решение:
Слайд 8
Непрерывная функция у = f(x) задана на отрезке [a;b]
На
рисунке изображен ее график. В ответе укажите количество точек графика
этой функции, в которых касательная параллельна оси Ох.y = f(x)
y
x
Ответ: 5
a
b
![Непрерывная функция у = f(x) задана на отрезке [a;b] На рисунке изображен ее график. В ответе укажите](/img/thumbs/ab19ed9f353efb9c260c88c0a268c1a9-800x.jpg "Применение производной к исследованию функций Непрерывная функция у = f(x) задана на отрезке [a;b] На рисунке")
Слайд 9
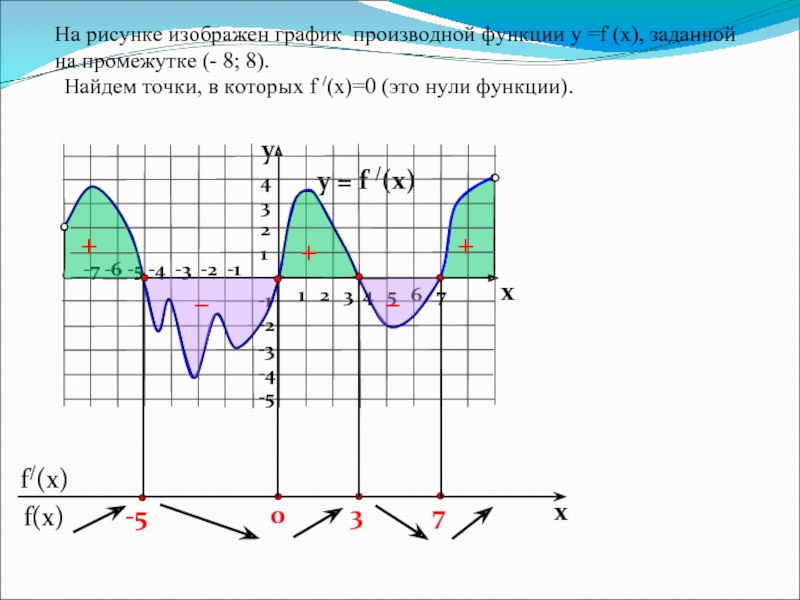
На рисунке изображен график производной функции у =f (x), заданной
на промежутке (- 8; 8).
y = f /(x)
1
2 3 4 5 6 7-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
Найдем точки, в которых f /(x)=0 (это нули функции).
+
–
–
+
+
Слайд 10
y = f /(x)
1 2 3 4
5 6 7
-7 -6 -5 -4 -3 -2
-14
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
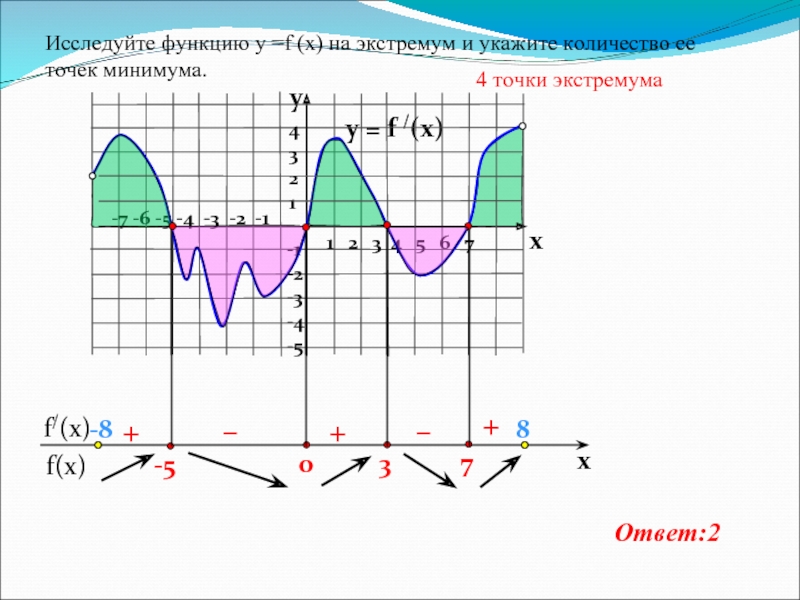
Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек минимума.
4 точки экстремума
Ответ:2
-8
8
Слайд 11
y = f /(x)
4
3
2
1
-1
-2
-3
-4
-5
y
x
+
–
–
+
+
Найдите количество точек экстремума функции у =f
(x)
на отрезке [– 3; 7]
Ответ: 3
1 2
3 4 5 6 7-7 -6 -5 -4 -3 -2 -1
-8
8
![y = f /(x) 4321-1-2-3-4-5yx+––++Найдите количество точек экстремума функции у =f (x) на отрезке [– 3; 7]Ответ: 31](/img/thumbs/9b8aa43d2a768409fa7e0bef0c067b0a-800x.jpg "Применение производной к исследованию функций y = f /(x) 4321-1-2-3-4-5yx+––++Найдите количество точек экстремума функции у =f (x)")
Слайд 12
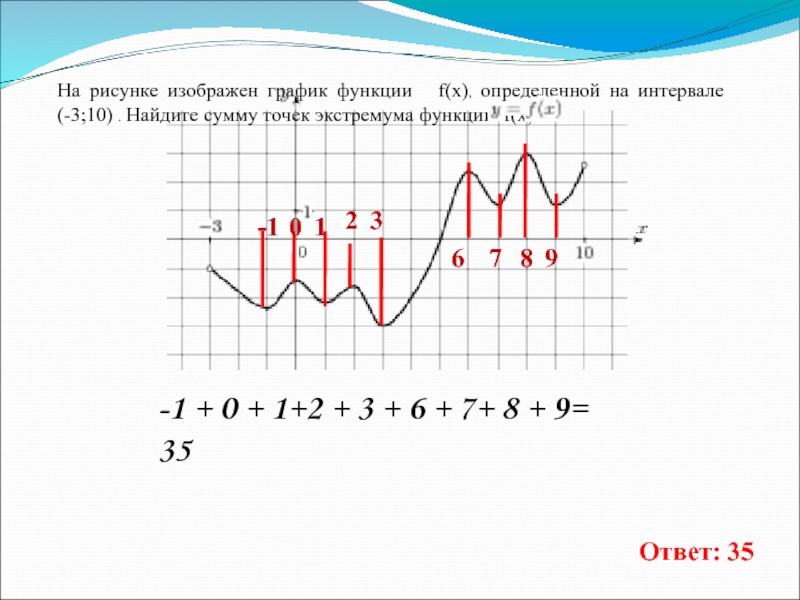
На рисунке изображен график функции f(x), определенной на интервале
(-3;10) . Найдите сумму точек экстремума функции f(x) .
-1
0
1
3
6
7
8
9
-1
+ 0 + 1+2 + 3 + 6 + 7+ 8 + 9= 35Ответ: 35
2
Слайд 13На рисунке изображен график y=f'(x) — производной функции f(x) ,
определенной на интервале (-8:5). В какой точке отрезка [-3;2]
принимает наибольшее значение?Ответ:-3
Слайд 14
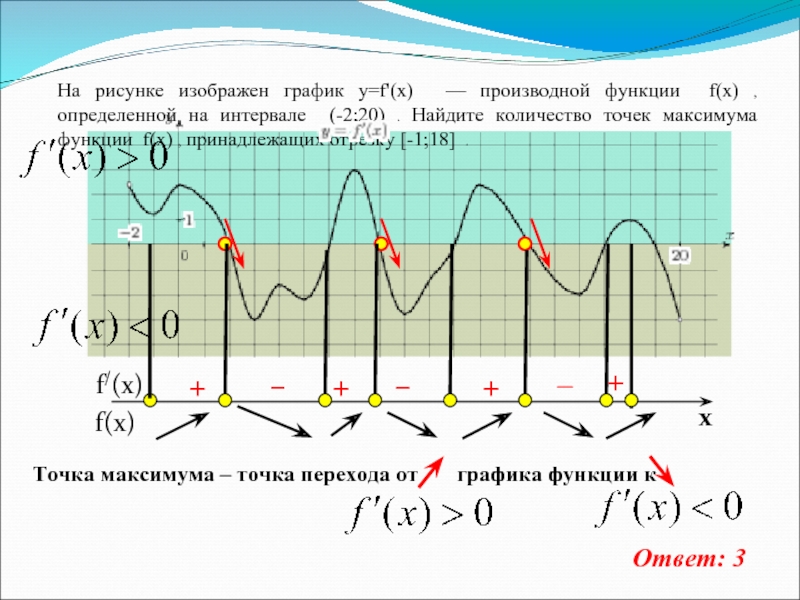
На рисунке изображен график y=f'(x) — производной функции f(x) ,
определенной на интервале (-2;20) . Найдите количество точек максимума функции
f(x) , принадлежащих отрезку [-1;18] .Ответ: 3
_
–
–
+
+
+
+
Слайд 15
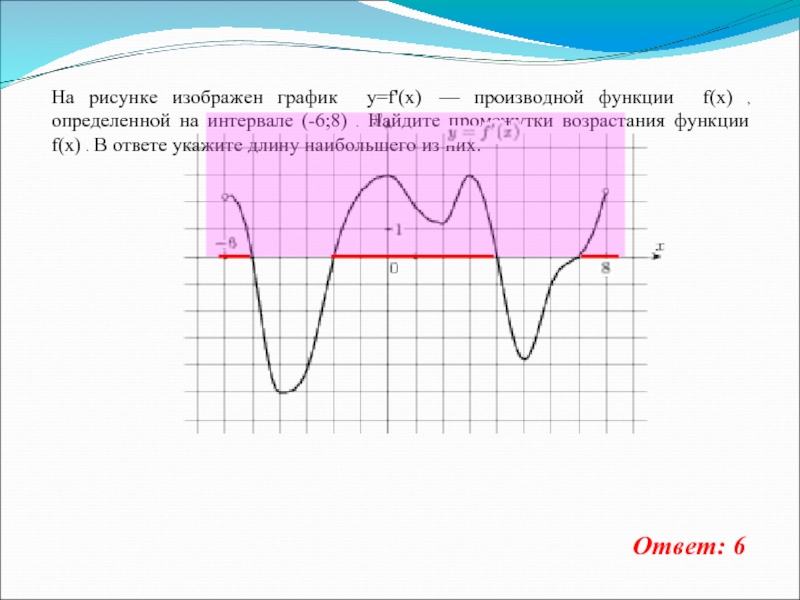
На рисунке изображен график y=f'(x) — производной функции f(x) ,
определенной на интервале (-6;8) . Найдите промежутки возрастания функции f(x)
. В ответе укажите длину наибольшего из них.Ответ: 6
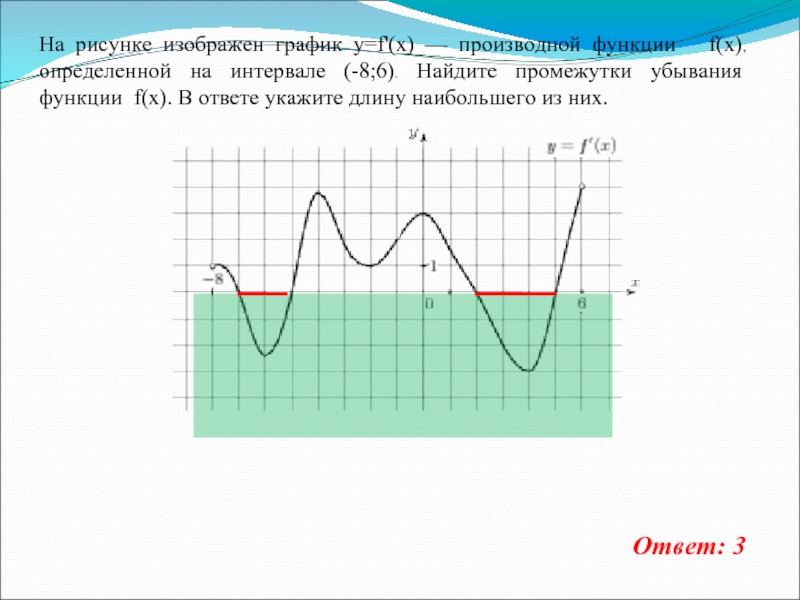
Слайд 16На рисунке изображен график y=f'(x) — производной функции f(x),
определенной на интервале (-8;6). Найдите промежутки убывания функции f(x). В
ответе укажите длину наибольшего из них.Ответ: 3
Теги
