Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производная 11 класс
Содержание
- 1. Производная 11 класс
- 2. СодержаниеИсторические сведенияОпределениеДифференцируемостьПравила дифференцированияПроизводная сложной функцииКасательная к графику
- 3. Исторические сведения
- 4. Определение производная функции f в точке x0
- 5. ДифференцируемостьФункция f, определенная на открытом интервале (a;b),
- 6. Правила дифференцирования сумма: (u + v)’ =
- 7. Производная сложной функции:Если функция f имеет производную
- 8. Касательная к графику функцииЕсли функция f в
- 9. Тангенс угла наклона касательной прямой Геометрический смысл
- 10. Производные тригонометрической и логарифмической функцииПроизводные тригонометрической функцииПроизводная логарифмической функции:
- 11. Скорость изменения функции Пусть s = s(t)
- 12. Схема исследования функций 1) Нахождение области определения2)
- 13. КОНЕЦСПАСИБОЗА ПРОСМОТР НАШЕЙ ПРЕЗЕНТАЦИИ!!!
- 14. Скачать презентанцию
СодержаниеИсторические сведенияОпределениеДифференцируемостьПравила дифференцированияПроизводная сложной функцииКасательная к графику функцииТангенс угла наклона касательной прямойПроизводные тригонометрической и логарифмической функцииСкорость изменения функцииСхема исследования функций
Слайды и текст этой презентации
Слайд 1Презентация
по алгебре
на тему:
Производная
Выполнили ученики 11 класса
МБОУ СОШ № 47 им.
В.А.Тамгина
Слайд 2Содержание
Исторические сведения
Определение
Дифференцируемость
Правила дифференцирования
Производная сложной функции
Касательная к графику функции
Тангенс угла наклона
касательной прямой
Производные тригонометрической и логарифмической функции
Скорость изменения функции
Схема исследования функций
Слайд 3Исторические сведения
Дифференциальное исчисление было
создано Ньютоном и Лейбницем в конце 17столетия на основе двух
задач:1) о разыскании касательной к произвольной линии
2) о разыскании скорости при произвольном законе движения
Еще раньше понятие производной встречалось в работах итальянского математика Тартальи (около 1500 - 1557 гг.) - здесь появилась касательная входе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда. В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л. Грегори. Большой вклад в изучение дифференциального
Слайд 4Определение
производная функции f в точке x0 называется число,
к которому стремится разность отношение
f = f (x0 + x)- f (x0)x x
при x, стремящемся к нулю
0
0
Слайд 5Дифференцируемость
Функция f, определенная на открытом интервале (a;b), является дифференцируемой на
(a;b) тогда и только тогда, когда f дифференцируема в каждой
точке этого интервала.Функция f в точке x дифференцируема тогда и только тогда, когда существует предел
lim D(h) = lim f(x0 = h) – f(x0)
h
Этот предел называется производной функции f в точке х или отношением дифференциалов в точке х
0
h 0
h 0
Слайд 6Правила дифференцирования
сумма: (u + v)’ = u’ + v’
коэффициент: (Cu)’ = Cu’
произведение: (uv)’ = u’v + uv’
частное: (u / v)'=(u'v - uv') / v2
Слайд 7Производная сложной функции:
Если функция f имеет производную в точке x0,
а функция g имеет производную в точке y0 = f(x0),
то сложная функция h(x) = g(f(x)) также имеет производную в точке x0, причем:Например: Найдем производную функции
Так как h(x) = g(f(x)), где
Слайд 8Касательная к графику функции
Если функция f в точке x0 дифференцируема,
то касательная к графику функции f в точке P0(x0;f(x0))
есть
прямая, проходящая через P0 и имеющая наклон m = f’(x0)Уравнение касательной к графику функции:
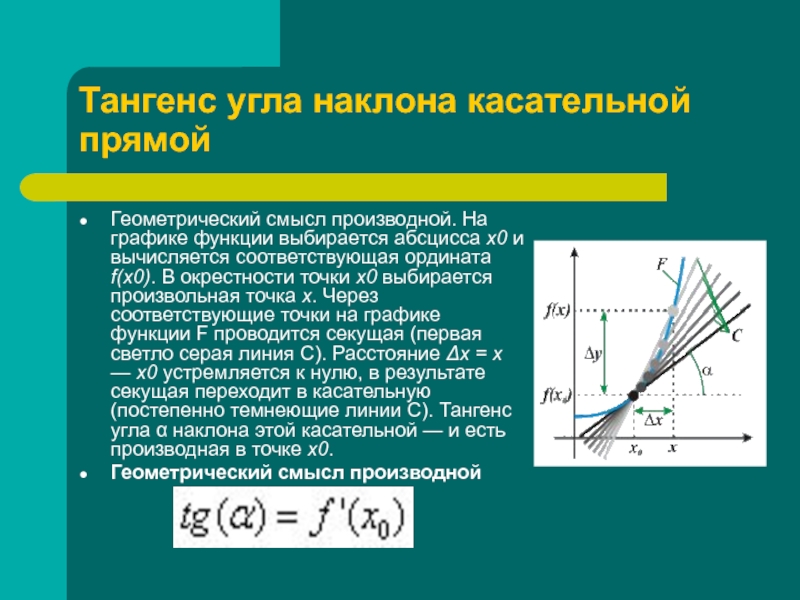
Слайд 9Тангенс угла наклона касательной прямой
Геометрический смысл производной. На графике
функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0). В
окрестности точки x0 выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло серая линия C). Расстояние Δx = x — x0 устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C). Тангенс угла α наклона этой касательной — и есть производная в точке x0.Геометрический смысл производной
Слайд 10Производные тригонометрической и логарифмической функции
Производные тригонометрической функции
Производная логарифмической функции:
Слайд 11Скорость изменения функции
Пусть s = s(t) — закон прямолинейного
движения. Тогда v(t0) = s'(t0) выражает мгновенную скорость движения в
момент времени t0. Вторая производная a(t0) = s''(t0) выражает мгновенное ускорение в момент времени t0.Вообще производная функции y = f(x) в точке x0 выражает скорость изменения функции в точке x0, то есть скорость протекания процесса, описанного зависимостью y = f(x).
Слайд 12Схема исследования функций
1) Нахождение области определения
2) Проверка на четность
/ нечетность
3) Нахождение точек пересечения с осями
4) Нахождение промежутков знакопостоянства
5)
Нахождение промежутков возрастания и убывания6) Нахождение точек экстремума и значений функции в этих точках
7) Исследование поведения функции в окрестностях «особых» точек и бесконечности