Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выпуклость графика функции. Точки перегиба 11 класс
Содержание
- 1. Выпуклость графика функции. Точки перегиба 11 класс
- 2. Цель и задачи урокаЦель: знакомство с второй
- 3. Ролевая игра «Один день из жизни делового человека»Импульс Энергия Позитив Шанс
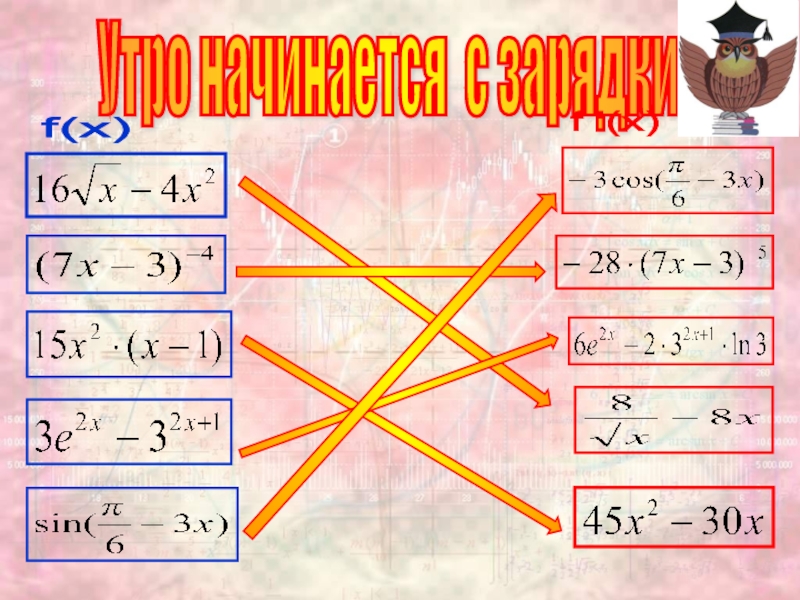
- 4. Утро начинается с зарядки f(x) f '(x)
- 5. Блиц- опрос1. При каких значениях х
- 6. Производная второго порядкаf (x) – функция
- 7. Точки перегибаЕсли f ‘‘(x) > 0, то
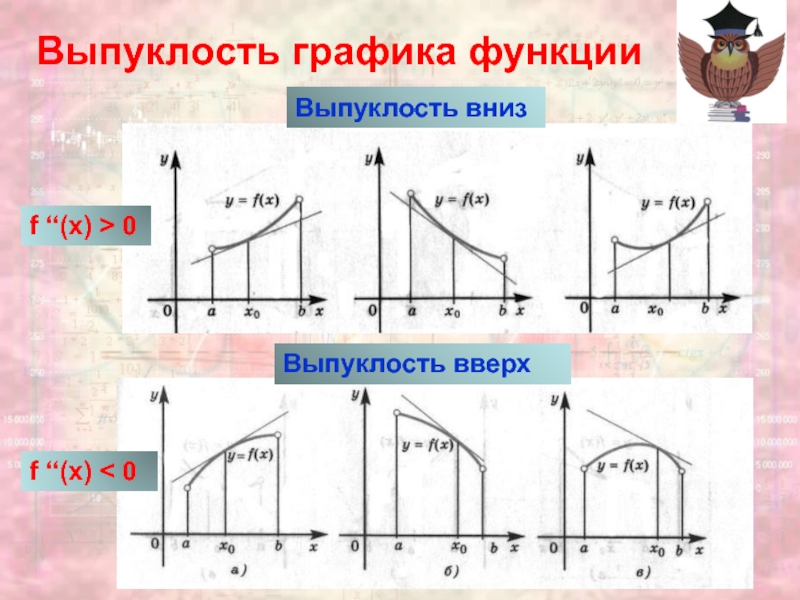
- 8. Выпуклость графика функцииВыпуклость внизВыпуклость вверхf ‘‘(x) > 0f ‘‘(x) < 0
- 9. 0f ’(x ) = -15 x4+ 15
- 10. Найти область определения функцииНайти первую производную функцииПриравнять
- 11. Составляющие успехаКомпетентностьПунктуальностьМобильностьПрактичностьТворческий подходКонструктивностьКреативностьОптимизм Коммуникабельность
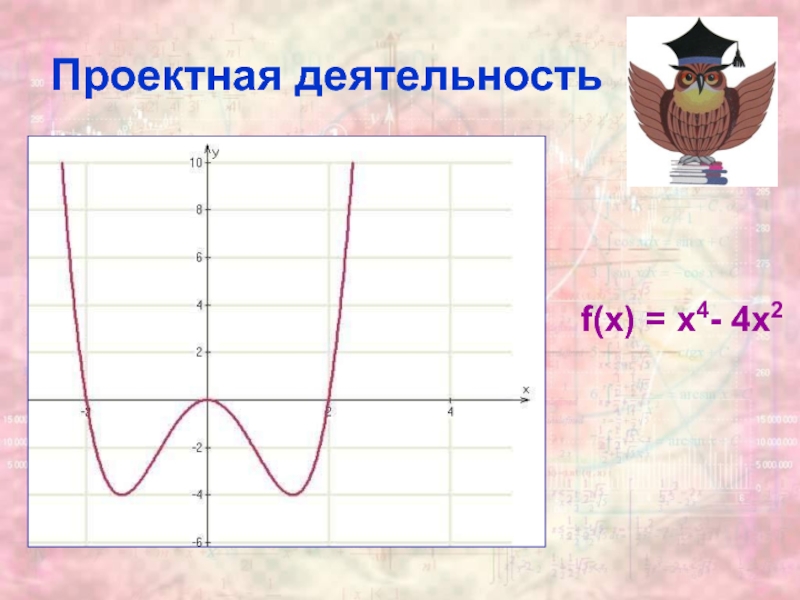
- 12. Проектная деятельность f(x) = x4- 4х2
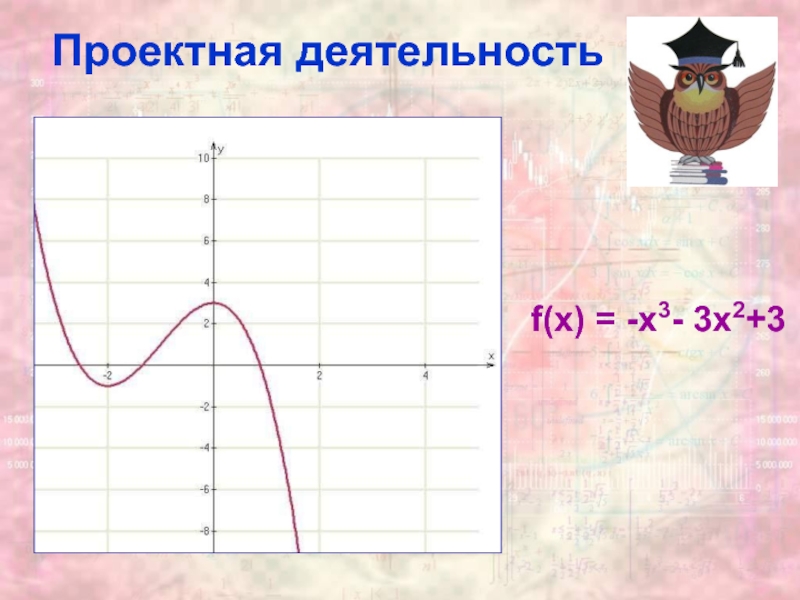
- 13. Проектная деятельность f(x) = -x3- 3х2+3
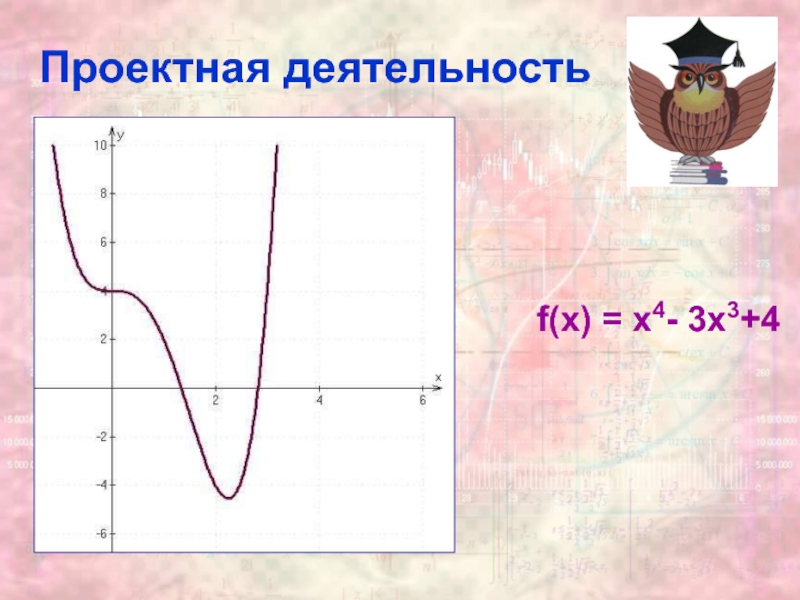
- 14. Проектная деятельность f(x) = х4- 3х3+4
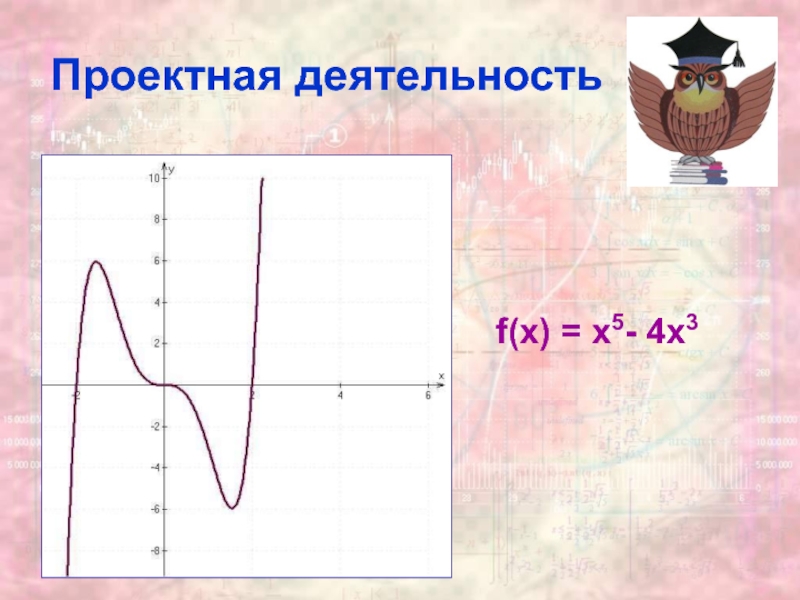
- 15. Проектная деятельность f(x) = x5- 4х3
- 16. Завершение работы - максимум успехаМаксимумИмпульсПозитивЭнергияШансБлагодарю за урок! Желаю удачи!
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Выпуклость графика функции. Точки перегиба.
Морозова
Наталия Александровна,
учитель математики
ГБОУ
средней школы № 164 Красногвардейского района
Слайд 2Цель и задачи урока
Цель: знакомство с второй производной функции и
её применением.
Задачи:
Нахождение производной второго порядка, определение точек перегиба и выпуклостей
графика функции при его построении.Воспитание умения работать в группах.
Применение полученных знаний для решения жизненных задач.
Слайд 5Блиц-
опрос
1. При каких значениях х функция возрастает?
2. Каков знак
производной функции на этих интервалах?
3. При каких значениях х функция
убывает?4. Каков знак производной функции на этом интервале?
5. Назовите точки экстремума.
6. Что происходит с производной функции в точках минимума и максимума?
7. Чему равно значение производной функции в точках экстремума?
8. Как проходит график касательной в точках экстремума?
9. Каков геометрический смысл производной функции?
Слайд 6Производная
второго порядка
f (x) – функция дифференцируема на (a;b)
f ‘
(x) – производная функции f(x) на (a;b)
f ‘‘ (x) –
вторая производная функции f(x) на (a;b)f ‘‘ (x) = (f ‘ (x)) ‘
f(x) = x3
f ‘(x) = 3x2
f “(x) = 6x
Слайд 7Точки перегиба
Если f ‘‘(x) > 0, то график функции выпуклый
вниз.
Если f ‘‘(x) < 0, то график функции выпуклый вверх.
х0 – точка перегиба дифференцируемой функции f (x), если в этой точке функция меняет направление выпуклости.
f(x) = x3
х0 = 0 (точка перегиба)
х0
Слайд 90
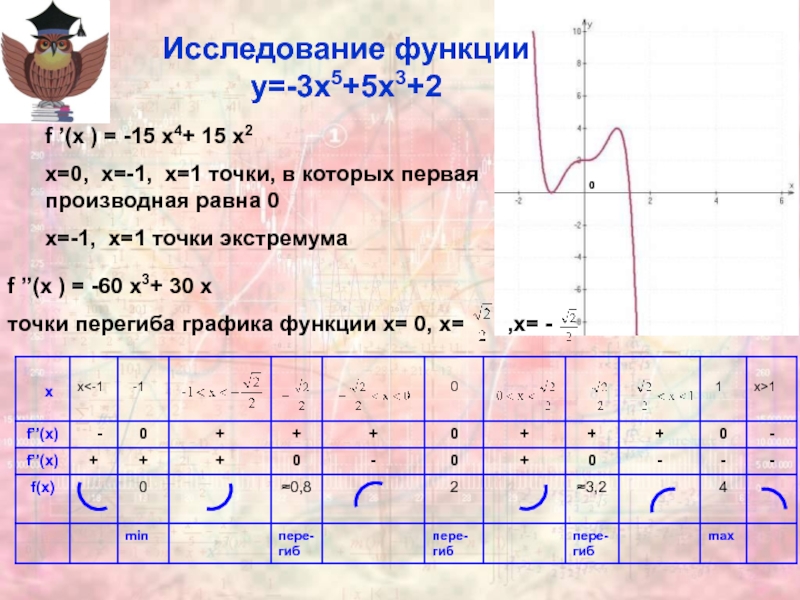
f ’(x ) = -15 x4+ 15 x2
x=0, x=-1, x=1
точки, в которых первая производная равна 0
x=-1, x=1 точки экстремума
Исследование функции
y=-3x5+5x3+2
Слайд 10Найти область определения функции
Найти первую производную функции
Приравнять первую производную к
нулю,
Найти стационарные точки,
Определить знаки первой производной
Определить промежутки возрастания
и убывания функцииНайти вторую производную функции
Приравнять вторую производную к нулю
Определить точки перегиба функции
Определить знаки второй производной на интервалах
Определить промежутки выпуклости графика функции
Найти значения функции в стационарных точках и точках перегиба
Данные внести в сводную таблицу
Найти корни функции и, если необходимо, дополнительные точки
Построить график функции
Алгоритм построения
графика функции: