Построение сечений многогранников 10 класс

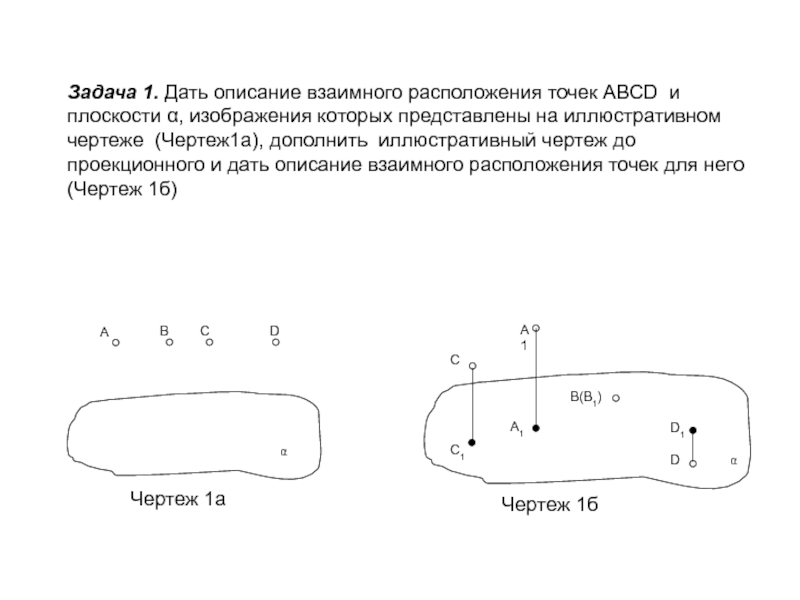
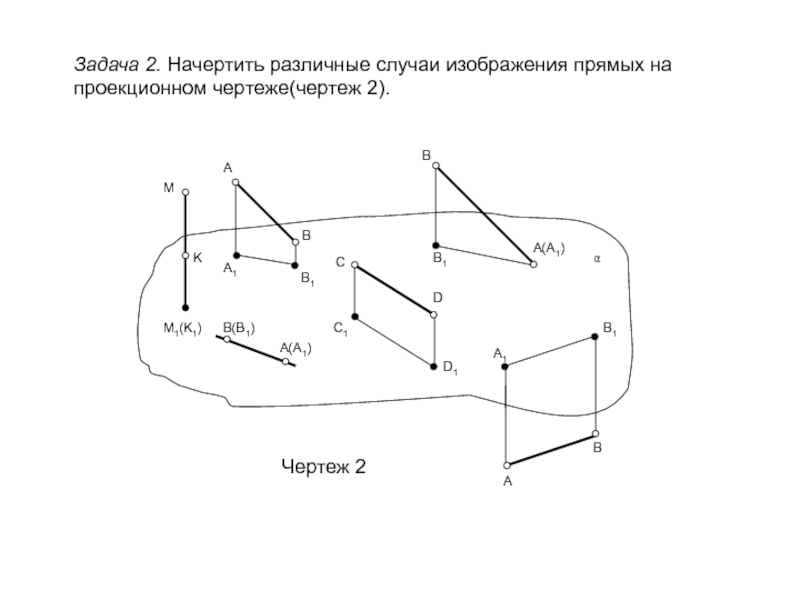
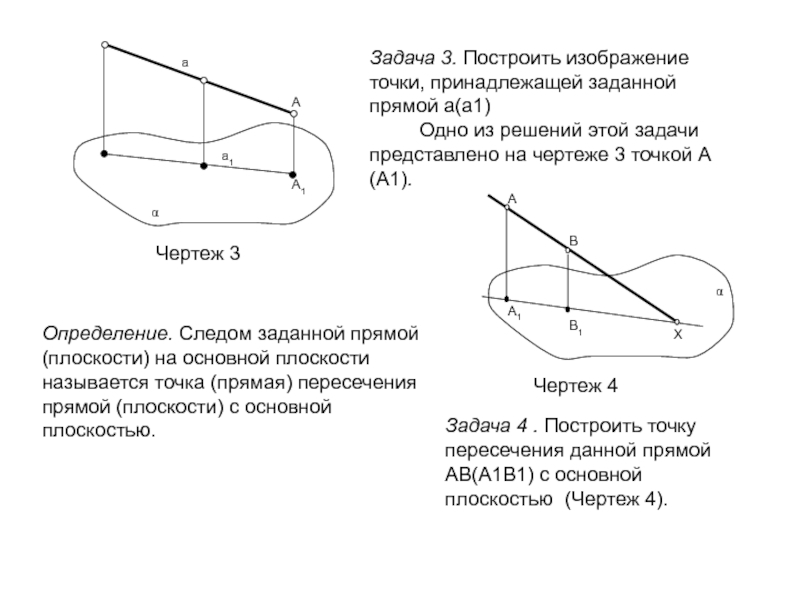
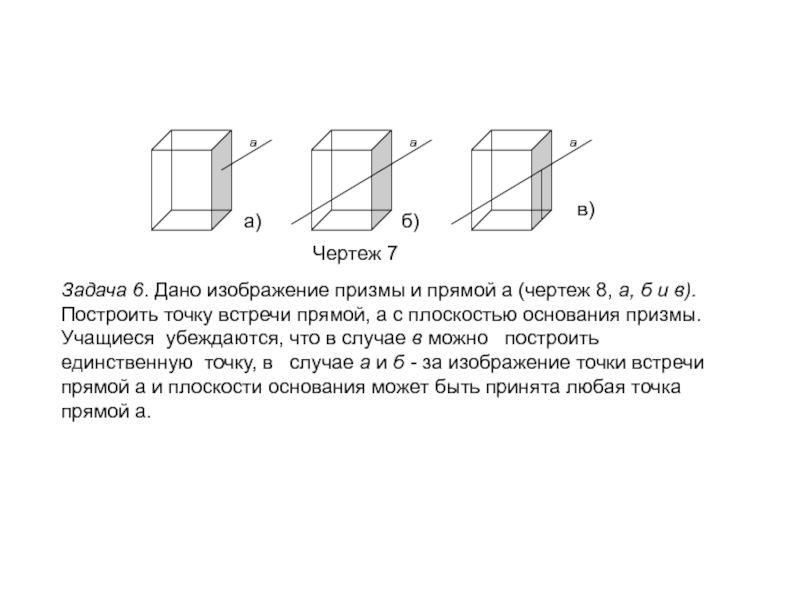
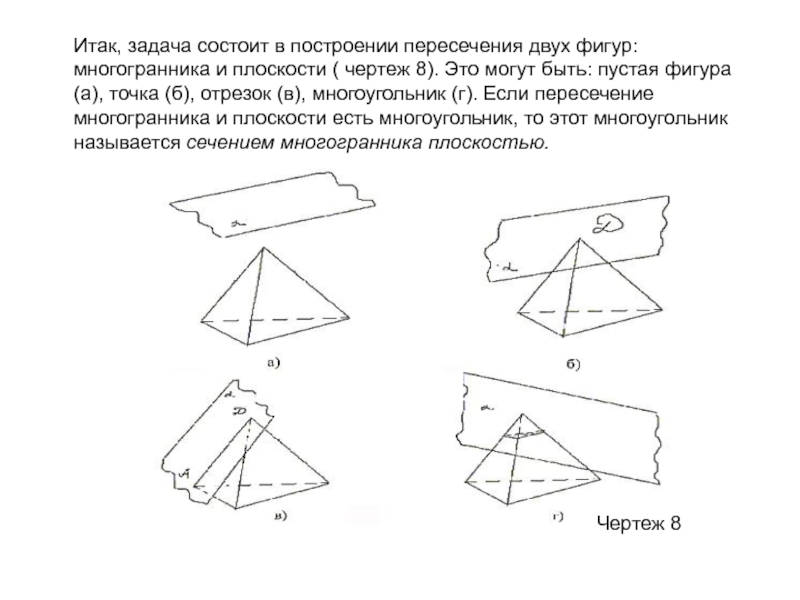
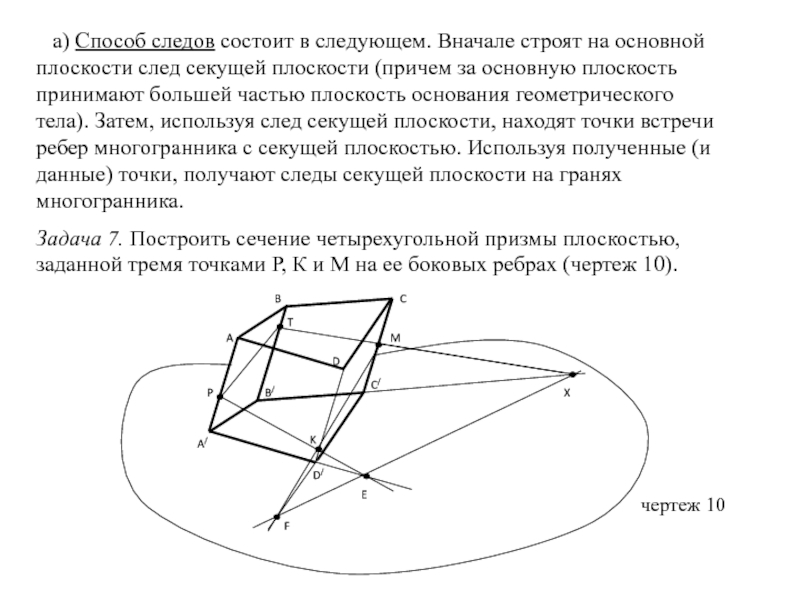
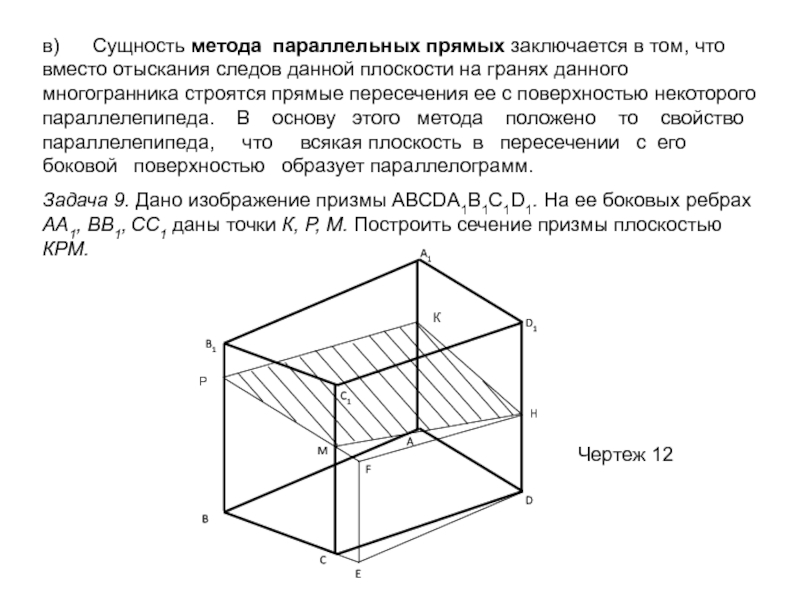
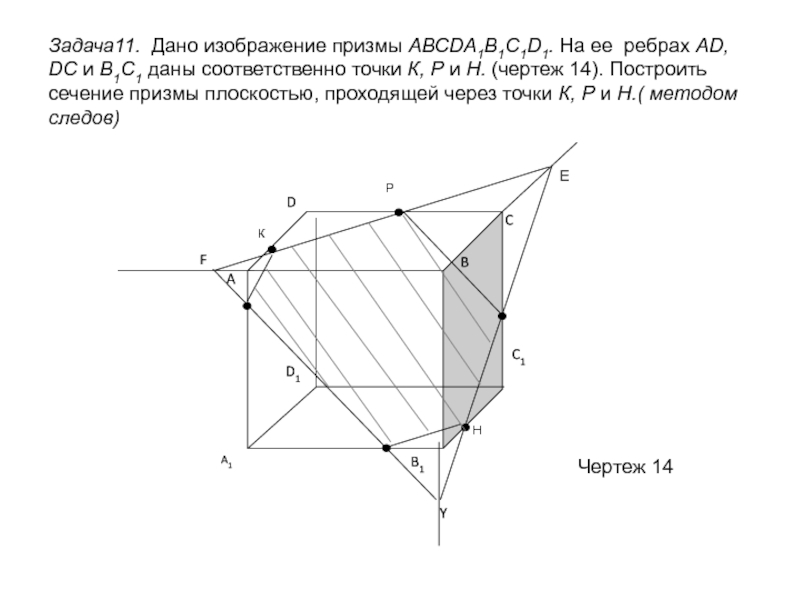
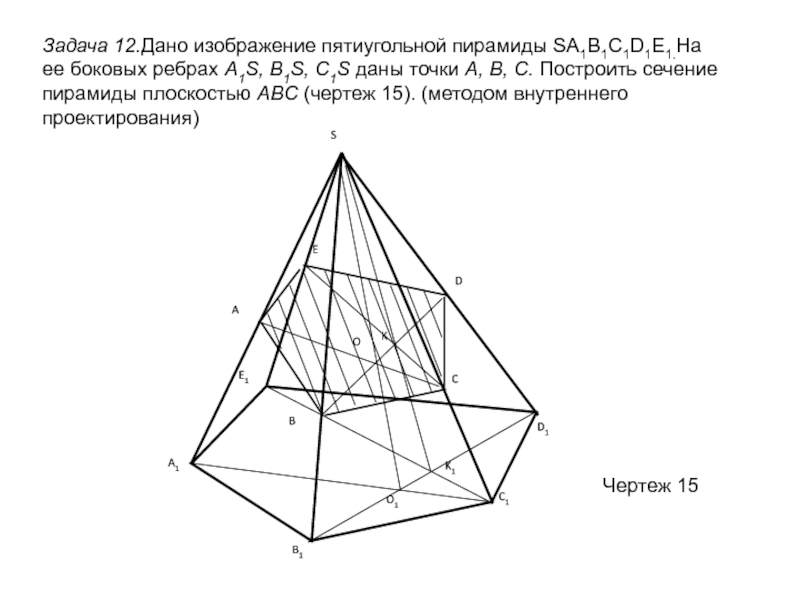
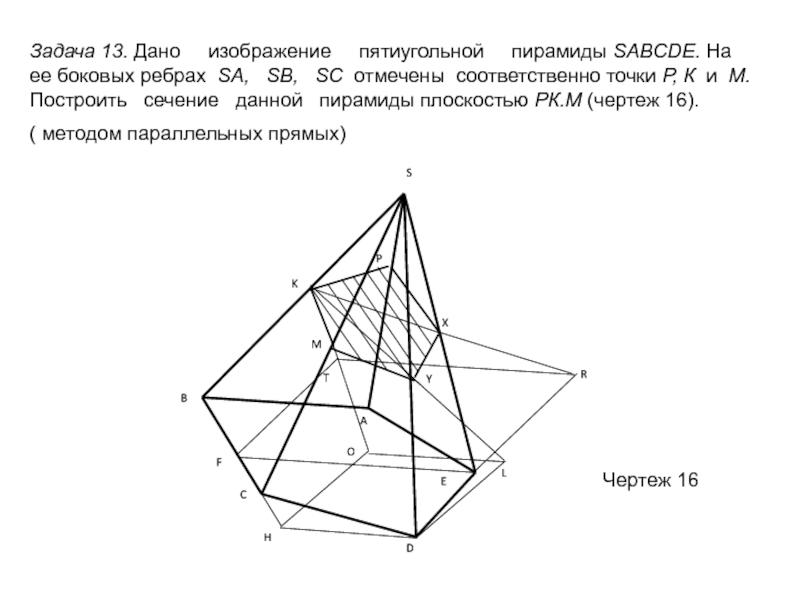
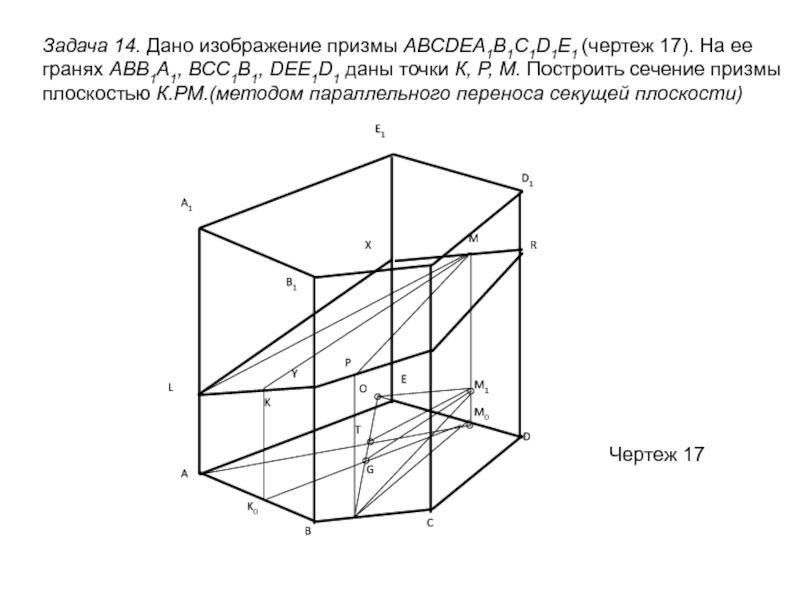
сечений; обобщить, систематизировать и закрепить полученные знания на предыдущих уроках;

ознакомиться с методами построений сечений многогранников;
Развивающая – развитие пространственного и образного мышления и воображения развитие мыслительных операций - обобщение, классификация и анализ;
Воспитательная – формирование графической культуры, воспитывать активность и самостоятельность, аккуратность, ответственность, уметь применять знания на практике, интерес к предмету;

 

плоскости ( чертеж 8). Это могут быть: пустая фигура (а),

точка (б), отрезок (в), многоугольник (г). Если пересечение многогранника и плоскости есть многоугольник, то этот многоугольник называется сечением многогранника плоскостью.

Чертеж 8

многоугольники получаются в сечении куба плоскостью? - может ли в

сечении куба плоскостью получиться семиугольник? А восьмиугольник и т.д.? Почему? Давайте рассмотрим призму и ее возможные сечения плоскостью ( на модели). Какие многоугольники получаются? -Какой можно сделать вывод? Чему равно наибольшее число сторон многоугольника, полученного сечением многогранника с плоскостью?

Чертеж 9

на основной плоскости след секущей плоскости (причем за основную плоскость

принимают большей частью плоскость основания геометрического тела). Затем, используя след секущей плоскости, находят точки встречи ребер многогранника с секущей плоскостью. Используя полученные (и данные) точки, получают следы секущей плоскости на гранях многогранника.
Задача 7. Построить сечение четырехугольной призмы пло­скостью, заданной тремя точками Р, К и М на ее боковых ребрах (чертеж 10).

чертеж 10

Имея три точки, определяющие плоскость сечения, находят их проекции

на основную плоскость, а также проекцию еще не построенной точки. По трем данным точкам и четырем проекциям отыскивают четвертую точку, принадлежащую плоскости сечения. Таким же образом, если это необходимо, получают пятую, шестую и т. д. точки, принадлежащие поверхности геометрического тела и плоскости сечения, т. е. сечению.
Задача 8.Дано изображение четырехугольной призмы. Построить ее сечение плоскостью, проходящей через точки А, В, С, лежащие на ребрах призмы (чертеж 11).

чертеж 11

что вместо отыска­ния следов данной плоскости на гранях данного многогранника

строятся прямые пересечения ее с поверхностью некоторого парал­лелепипеда. В основу этого метода положено то свойство параллелепипеда, что всякая плоскость в пересечении с его боковой поверхностью образует параллелограмм.
Задача 9. Дано изображе­ние призмы АВСDA1B1C1D1. На ее боковых ребрах АА1, ВВ1, СС1 даны точки К, Р, М. Построить сечение призмы плоскостью КРМ.

К

Р

Чертеж 12

в следующем: строится такое вспомогательное сечение данного многогранника, которое удовлетворяет

следующим требованиям:
1) оно должно быть параллельно секущей плоскости;
2) в пересечении с поверхностью данного многогранника образуется треугольник.
После этого искомое сечение строится на основании свойств прямых, по которым две параллельные плоскости пересекаются третьей плоскостью.

На ее боковых ребрах SA, SB, SE отмечены соот­ветственно точки

К, М, Р. Построить сечение этой пирамиды плоскостью КМР.

и В1С1 даны соответственно точки К, Р и Н. (чертеж

14). Построить сечение призмы плоскостью, проходящей через точки К, Р и Н.( методом следов)

Чертеж 14

B1S, C1S даны точки А, В, С. Построить сечение пирамиды

плоскостью ABC (чертеж 15). (методом внутреннего проектирования)

Чертеж 15

пирамиды SABCDE. На ее боковых ребрах SA, SB,

SC отмечены соответственно точки Р, К и М. Построить сечение данной пирамиды плоскостью РК.М (чертеж 16).
( методом параллельных прямых)

Чертеж 16

гранях АВВ1А1, ВСС1В1, DEE1D1 даны точки К, Р, М. Построить

сечение призмы плоскостью К.РМ.(методом параллельного переноса секущей плоскости)

Чертеж 17

сечения многогранников?
В чем сущность метода следов ?
В чем сущность метода

внутреннего проектирования?
В чем сущность метода параллельных прямых ?
В чем сущность метода переноса секущей плоскости?

Домашнее задание.
Составить четыре задачи на построение сечений многогранников с использованием полученных знаний.

 

для 8-9 классов: Учеб. пособие для учащихся шк. и классов

с углубл. изуч. математики. - М.: Просвещение, 1991.
2. Аргунов Б. И. Преобразования плоскости. - М.: Просвещение, 1976.
3 . Атаносян Л.С., Базылев В.Т. Геометрия. В 2-х ч. Ч. 1 . Учебное пособие для физико-математических факультетов педагогических институ­тов. - М.: Просвещение, 1986.
5. Бескин Н. М. Изображение пространственных фигур.
6. Болтянский В.Г. Элементарная геометрия: Книга для учителя. - М.: Просвещение, 1985.
7. Вересова Е.Е. и др. Практикум по решению математических задач: Учеб. пособие для пед. ин-тов. - М.: Просвещение, 1979.
8.Полякова Т.С. Методика обучения геометрии в основной школе: Учебное пособие для студентов педвузов и педколледжей. - Ростов н/Д: РГПУ, 2000.