Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
"Примеры комбинаторных задач 9 класс"
Содержание
- 1. "Примеры комбинаторных задач 9 класс"
- 2. Что изучает комбинаторика? Комбинаторикой называют область математики,
- 3. Страничка истории Комбинаторные мотивы можно заметить
- 4. Страничка истории Хрисипп Гиппарх Аристотель
- 5. В XII веке индийский математик Бхаскара в своём основном труде «Лилавати»
- 6. Страничка истории (Новое время) Джераламо Кордано написалматематическое
- 7. Треугольник Паскаля бесконечная таблица
- 8. Пример 1. Сколько существует двузначных чисел?Первой цифрой
- 9. Пример 2 Сколько существует пятизначных чисел, которые
- 10. Комбинаторное правило умножения: Пусть имеется n элементов
- 11. Пример 3. В спортивных соревнованиях участвуют
- 12. Факториал Произведение подряд идущих первых n натуральных
- 13. Заполни таблицу:
- 14. Проверка: 1! = 12! = 1•2 =
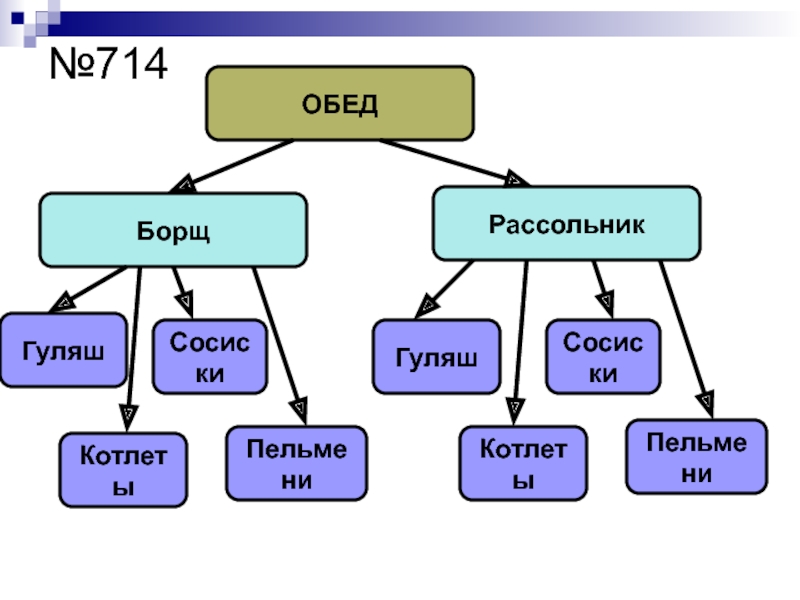
- 15. №714 ОБЕДБорщРассольникГуляшКотлетыСосискиПельмениГуляшКотлетыСосискиПельмени
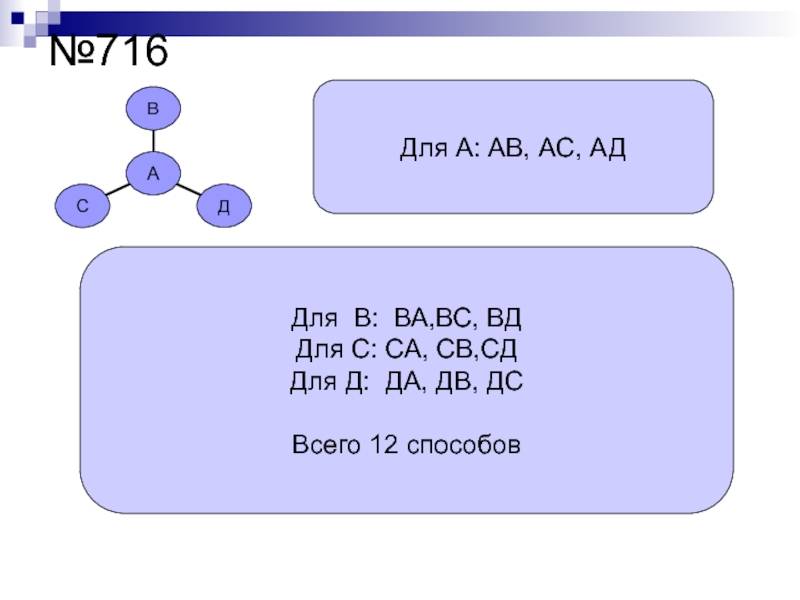
- 16. №716 Для А: АВ, АС, АДДля В:
- 17. СамостоятельноПроверка
- 18. Проверка
- 19. Домашнее задание №715,718(б), 720,727
- 20. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Примеры комбинаторных задач
Никитина Елена Анатольевна
учитель математики
I кв. категория
МБОУ
«Средняя общеобразовательная школа №2 им.Е.В. Камышева» г.Гагарин Смоленской области
Слайд 2Что изучает комбинаторика?
Комбинаторикой называют область математики, изучающую вопросы о
числе различных комбинаций (удовлетворяющих тем или иным условиям), которые можно
составить из данных элементов.Слайд 3
Страничка истории
Комбинаторные мотивы можно заметить в символике китайской «Книги
Перемен»
(V век до н. э.).
По мнению её авторов, всё в мире комбинируется из различных сочетаний мужского и женского начал, а также восьми стихий: земля, горы, вода, ветер, гроза, огонь, облака и небо. Большой интерес математиков многих стран с древних времён неизменно вызывали магические квадраты. Гексаграмма из
«Книги перемен»
Магический квадрат
на гравюре Дюрера
Альбрехт Дюрер
Слайд 4Страничка истории
Хрисипп
Гиппарх
Аристотель
Античные греки также
рассматривали отдельные комбинаторные задачи, хотя систематическое изложение ими этих вопросов,
если оно и существовало, до нас не дошло. Хрисипп (III век до н.э) и Гиппарх (II век до н. э.)подсчитывали, сколько следствий можно получить
из 10 аксиом; методика подсчёта нам неизвестна,
но у Хрисиппа получилось более миллиона,
а у Гиппарха — более 100000.
Аристоксен
Аристотель при изложении своей логики
безошибочно перечислил все
возможные типы трёхчленных силлогизмов.
Аристоксен рассмотрел различные
чередования длинных и коротких слогов
в стихотворных размерах.
Слайд 5В XII веке индийский математик
Бхаскара в своём основном труде
«Лилавати» подробно исследовал
задачи,
связанные с перестановками
и сочетаниями, включая перестановки
с повторениями. В
ЗападнойЕвропе ряд глубоких открытий в
области комбинаторики сделали
два еврейских исследователя,
Авраам ибн Эзра (XII век) и
Леви бен Гершом и др.
Несколько комбинаторных задач
содержит «Книга абака»
(Фибоначчи, XIII век).
Например, он поставил задачу
найти наименьшее число гирь,
достаточное
для взвешивания любого
товара весом от 1 до 40 фунтов.
Страничка истории
Леона́рдо
Пиза́нский
Наиболее
известен
под прозвищем
Фибона́ччи
Страница
из
Книги абака
Слайд 6
Страничка истории
(Новое время)
Джераламо Кордано написал
математическое исследование
игры в кости.
Историей
игры занимались
Тарталья и Галилео
Галилей.
В историю зарождавшейся теории
вероятностей вошла
переписка заядлого игрока шевалье де Мерэ с Пьером
Ферма и Блезом Паскалем, где были затронуты
несколько тонких комбинаторных вопросов.
Блез Паскаль много занимался
биномиальными коэффициентами
и открыл простой способ их вычисления:
«Треугольник Паскаля»
Сам термин «комбинаторика»
придумал Лейбниц, который в 1666 году
(ему было тогда 20 лет) опубликовал книгу
«Рассуждения о комбинаторном искусстве».
Якоб Бернулли – один из основоположников теории вероятностей.
Паскаль- ввел термин «сочетание». Абрахам де
Муавр и Джеймс Стирлинг занимались вопросом факториала.
Д
а
л
е
е
Слайд 7
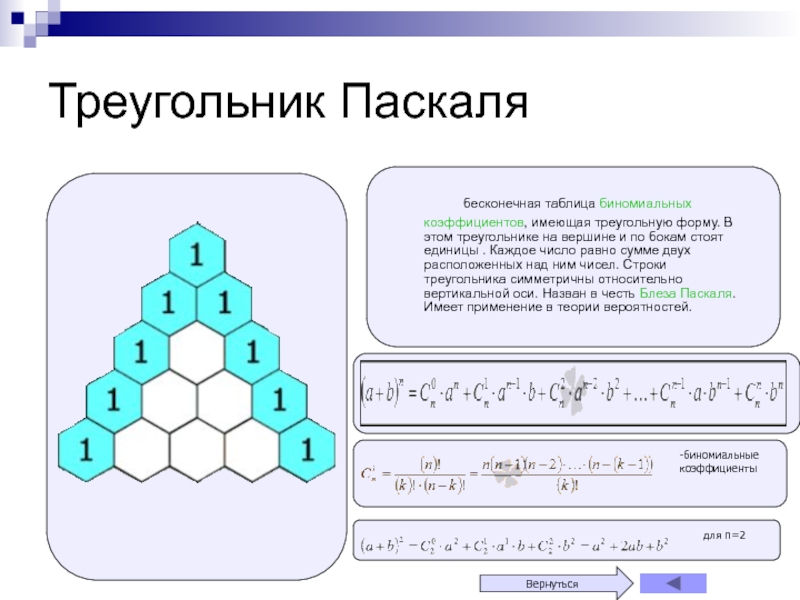
Треугольник Паскаля
бесконечная таблица биномиальных коэффициентов, имеющая
треугольную форму. В этом треугольнике на вершине и по бокам
стоят единицы . Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля. Имеет применение в теории вероятностей.-биномиальные
коэффициенты
для n=2
Вернуться
Слайд 8Пример 1.
Сколько существует двузначных чисел?
Первой цифрой могут быть 1,2,3,4,5,6,7,8,9
1
0
1 2
3 4 5 6 7 8 9Аналогично, если первая цифра 2,3,4,5,6,7,8,9.
Получаем 9 • 10= 90 вариантов
это числа:
10,11,12,13………………97,98,99.
Слайд 9Пример 2
Сколько существует пятизначных
чисел, которые читаются
одинаково слева
направо
и справа налево?
На первом месте цифры 1,2,3,4…9.
(9 вариантов)
На втором
и предпоследнем месте любая цифра (10 вариантов)На третьем месте ( в середине) любая цифра (10 вариантов)
9 • 10 • 10 = 900 вариантов (чисел)
Слайд 10Комбинаторное правило умножения:
Пусть имеется n элементов и нужно выбрать
из
них один за другим к элементов.
Если первый элемент
можно выбрать n1 способом,второй элемент можно выбрать n2 способом,
третий элемент можно выбрать n3 способом,
и так далее…., то число способов, которыми могут
быть выбраны к элементов равно произведению
n1•n2•n3•…….•nк
Слайд 11Пример 3.
В спортивных соревнованиях участвуют 10 команд. Сколькими
способами могут
Быть распределены золотая, серебряная и бронзовая медали, если любая
команда может получить только одну медаль?
Бронза n1 = 10
Серебро n2= 9
Золото n3 = 8
n1 • n2 • n3 = 10 • 9 • 8 = 720
Слайд 12Факториал
Произведение подряд идущих
первых n натуральных
чисел называют факториал
Читается:«
эн факториал»
Обозначение:
n! = 1•2•3•4•……•n
Пример:
5! = 1•2•3•4•5 =120
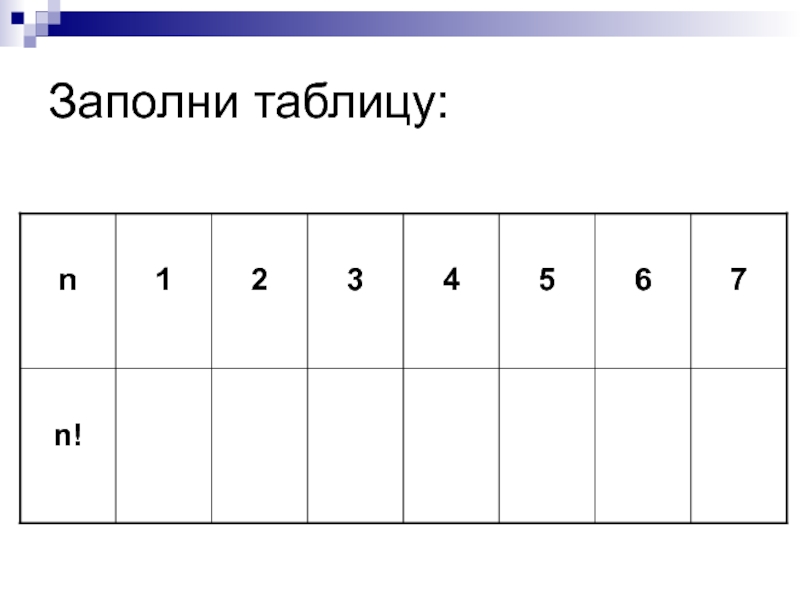
Слайд 14Проверка:
1! = 1
2! = 1•2 = 2
3! = 1•2•3
= 2!• 3 = 6
4! = 1•2•3•4 = 3!•4 =
245! = 1•2•3•4•5 = 4!•5 = 120
6! = 1•2•3•4•5•6 = 5!•6 = 720
7! = 1•2•3•4•5•6•7= 6!•7=5040