Слайд 1ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ ГОРОДА МОСКВЫ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА
С УГЛУБЛЁННЫМ ИЗУЧЕНИЕ
ИНОСТРАННЫХ ЯЗЫКОВ
№1373
Исследовательский проект
«О РАЗРЕШИМОСТИ КУБИЧЕСКИХ УРАВНЕНИЙ В РАДИКАЛАХ»
Авторы проекта:
Быкова
Екатерина Андреевна,
Пучкова Анастасия Николаевна,
Романова Наталья Алексеевна.
Руководитель проекта –
Романова Татьяна Витеславовна,
учитель математики.
Слайд 2Цели работы: популяризация математических знаний, нахождение наиболее простых способов решения
уравнений 2-ой и 3-ей степеней
Задачи работы:
проведение конкурса рефератов «Знаменитые
математики, внёсшие значительный вклад в решение кубических уравнений»;
расширение знаний учащихся о множествах чисел, знакомство с мнимой единицей и множеством комплексных чисел;
проведение обобщающего урока по теме «Решение уравнений 1-ой и 2-ой степеней по формулам»;
проведение семинара «Вывод формулы для решения уравнений 3-ей степени» с привлечением выпускников школы, обучающихся в технических вузах;
выяснение прикладного значения формулы Кардано;
разрешение вопроса о возможности решения уравнений 4-ой и 5-ой степеней по формулам
Слайд 3Папирус Райнда и Московский папирус
Оба папируса относятся к XVIII веку
до н. э. В них даны примеры элементарных арифметических расчётов,
задачи отвлечённого и конкретного содержания “по разделу хлебов”, вычислению площадей полей, вместимости круглых и прямоугольных корзин, вычислению пирамид. В папирусах даётся лишь ход решения задач; правил, обоснований и обобщений нет.
Слайд 4Вавилонская математика
II тысячелетие до н.э. В математических текстах, выполненных клинописью
на глиняных пластинках, есть квадратные и биквадратные уравнения, системы уравнений
с двумя неизвестными и даже простейшие кубические уравнения. Задачи носили учебный характер, не было обобщений и доказательств.
Слайд 5Геометрическая алгебра греков
Создана математическая теория, в математику включены логические доказательства,
отдельные её части стали строиться как дедуктивный метод.
Слайд 6Мухаммед ал-Хорезми, Омар Хайям
1048 – 1131 гг.
Трактат ”Китаб аль-джебр валь-мукабала”.
Общие
правила для решения уравнений первой степени, квадратные уравнения различных видов,
правила алгебраических преобразований.
“Трактат о доказательстве задач алгебры”.
Дано определение алгебры как науки о решении уравнений.
Слайд 7Линейные уравнения
Уравнение вида ax = b, где х – переменная,
a и b – некоторые числа, называется линейным уравнением с
одной переменной.
Линейное уравнение ax = b, при a ≠ 0 имеет один корень, при a = 0 и b ≠ 0 не имеет корней, а = 0 и b = 0 имеет бесконечно много корней (любое число является его корнем).
Слайд 8Задача Метродора
Здесь погребен Диофант, и камень могильный
При счёте искусном расскажет
нам, сколь долог был его век.
Велением бога он мальчиком был
шестую часть своей жизни;
В двенадцатой части затем прошла его светлая юность.
Седьмую часть жизни прибавим – перед нами очаг Гименея .
Пять лет протекли; и прислал Гименей ему сына.
Но горе ребёнку! Едва половину он прожил
Тех лет, что отец, как скончался несчастный.
Четыре года страдал Диофант от утраты такой тяжёлой
И умер, прожив для науки. Скажи мне,
Скольких лет достигнув, смерть восприял Диофант?
Слайд 9Квадратные уравнения
Квадратным называют алгебраическое уравнение 2-й степени, т.е. уравнение вида
ах² + bx + c = 0, где а ≠0.
Выражение
D = b² - 4ac называют дискриминантом квадратного трёхчлена ax² + bx + c.
Уравнение имеет два корня: х = , х = ,
а для уравнения с четным коэффициентом при х формула принимает вид
х = , x = , где к = , D1 = к2 – ас.
Слайд 10Сципион дель Ферро
Итальянский математик, открывший общий метод решения неполного кубического
уравнения.
Дель Ферро закончил Болонский университет, после чего работал там профессором
математики до конца жизни.
1465 – 1526 гг.
Слайд 11Николо Тарталья
Итальянский математик, родился в Брешии. В 1512 году, во
время взятия Брешии французами, он получил рану в нижнюю часть
лица, вследствие которой произношение его стало неправильным.
Поэтому товарищи прозвали его заикой (по-итальянски «tartaglia») и прозвище это сделалось его фамилией. Настоящая фамилия Фонтана.
1500 – 1557 гг.
Слайд 12Математический турнир между Тартальей и Фиоре
Для участников алгебраических диспутов было
важно обладать неизвестной ещё для других формулой решения того или
иного типа уравнений, алгоритмом, с помощью которого можно было решить значительное количество задач.
Слайд 13Джероламо Кардано
Итальянский математик, инженер, философ, медик и астролог.
Учился в университетах
Павии и Падуи. Сначала занимался только медициной, но в 1534
году стал профессором математики в Милане, позже – в Болонье. Однако, Кардано не бросил врачебное занятие.
1501 – 1576 гг.
Слайд 14Кардано внёс значительный вклад в развитие алгебры: его имя носит
формула Кардано для нахождения корней кубического уравнения.
Согласно легенде, Кардано предсказал
дату своей смерти и, чтобы оправдать свое предсказание, сам уморил себя голодом.
Слайд 15Лодовико (Луиджи) Феррари
Родился в Болонье. Итальянский математик, нашел общее решение
уравнения четвертой степени.
Уже в восемнадцать лет Феррари стал профессором
Миланского университета, однако потом вернулся в родной город, где также стал профессором математики.
1522 – 1565 гг.
Слайд 16Вывод формулы Кардано
Рассмотрим уравнение x³ + px + q =
0
Введем новые неизвестные x = u + v; получим
u³ +
v³ + (3uv + p)(u + v) +q = 0
Приравняем 3uv + p нулю
u³ + v³ + q = 0.
Тогда
uv = -
u³v³ = -
u³ + v³ = - q.
Выражения u и v можно принять за корни квадратного уравнения z² + qz - = 0. Решая его, получим
z = -
Таким образом,
x = u + v = +
Слайд 17Комплексные числа
Комплексными числами называются числа вида a + bi, где
a и b – действительные числа, а i – число
особого рода, квадрат которого равен -1, т. е. i² = -1. Действия над комплексными числами выполняются по таким же правилам, что и над многочленами, при этом i² заменяют на -1.
z = a + bi
a – действительная часть («reel» - реальный, действительный)
Re z = a
b – мнимая часть («imaginaire» – мнимый, воображаемый)
Im z = b
Слайд 18Нахождение формулы для решения уравнений 5-ой степени
Ж.Лагранж, П. Руффини, Н.
Абель
Не существует формулы, с помощью которой можно выразить корни любого
уравнения 5-ой степени через коэффициенты уравнения, используя лишь арифметические операции и извлечение корней.
Слайд 19Выдающийся французский математик, основатель современной алгебры.
В возрасте 12 лет Эварист
покинул родительский дом и поступил в Королевский коллеж Луи-ле-Гран (ныне
лицей), где читал серьёзные математические сочинения. В числе прочих ему попался мемуар Нильса Абеля о решении уравнений произвольной степени. Тема захватила Галуа, и он начинает собственные исследования.
1811 – 1832 гг.
Эварист Галуа
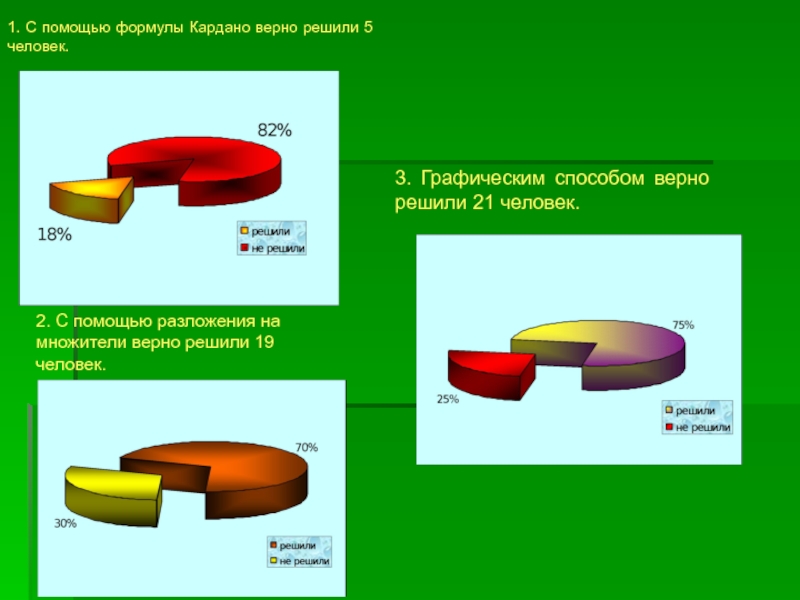
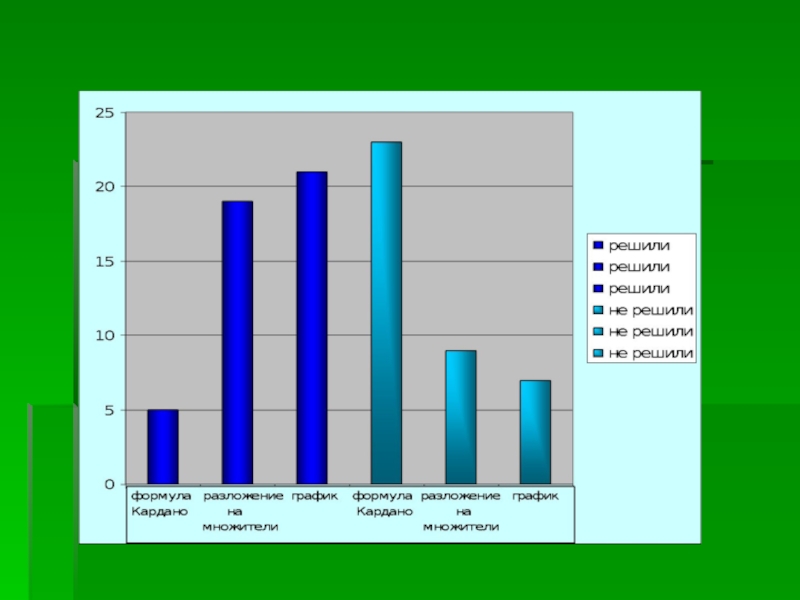
Слайд 201. C помощью формулы Кардано верно решили 5 человек.
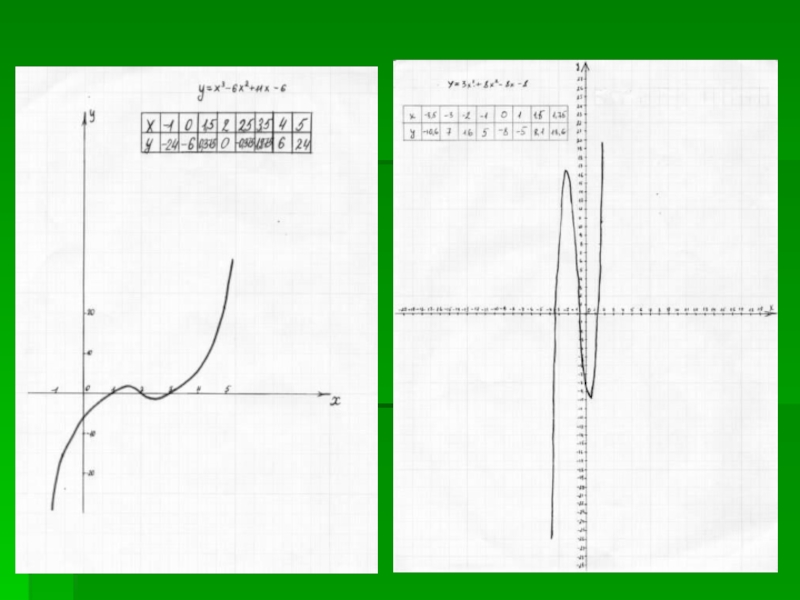
3. Графическим
способом верно решили 21 человек.
2. С помощью разложения на
множители верно решили 19 человек.
Слайд 23Выводы
В ходе работы над проектом мы провели конкурс рефератов «Знаменитые
математики, внесшие значительный вклад в решение кубических уравнений» для учеников
нашего класса. Авторы лучших рефератов представили свои работы учащимся седьмых классов.
Усилиями нашей творческой группы был проведен урок «Решение квадратных уравнений на множестве комплексных чисел». На этом уроке мы познакомили наших одноклассников с комплексными числами, показали, что любое квадратное уравнение имеет два корня на множестве комплексных чисел.
В рамках проведения недели математики мы организовали такой урок в параллели девятых классов, показали презентацию нашего проекта учащимся десятых и одиннадцатых классов.