Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1 Метод векторных диаграмм – представление гармонических колебаний с помощью
Содержание
- 1. 1 Метод векторных диаграмм – представление гармонических колебаний с помощью
- 2. Сложение колебаний с одинаковыми частотами Тело участвует
- 3. б) Сложение колебаний с разными частотами и
- 4. Электрический колебательный контурЭлектрический колебательный контур - электрическая
- 5. При R = 0 - колебания незатухающие,
- 6. а) Свободные незатухающие колебания возникают в идеальном
- 7. Слайд 7
- 8. Решение : - амплитуда колебаний заряда;Период колебаний:-
- 9. Напряжение на конденсаторе по определению :- волновое
- 10. б) Свободные затухающие колебания : R
- 11. Сравнение характеристик колебательных процессов пружинного маятника и колебательного контура
- 12. в) Вынужденные электрические затухающие колебания: еслиилиРешение :
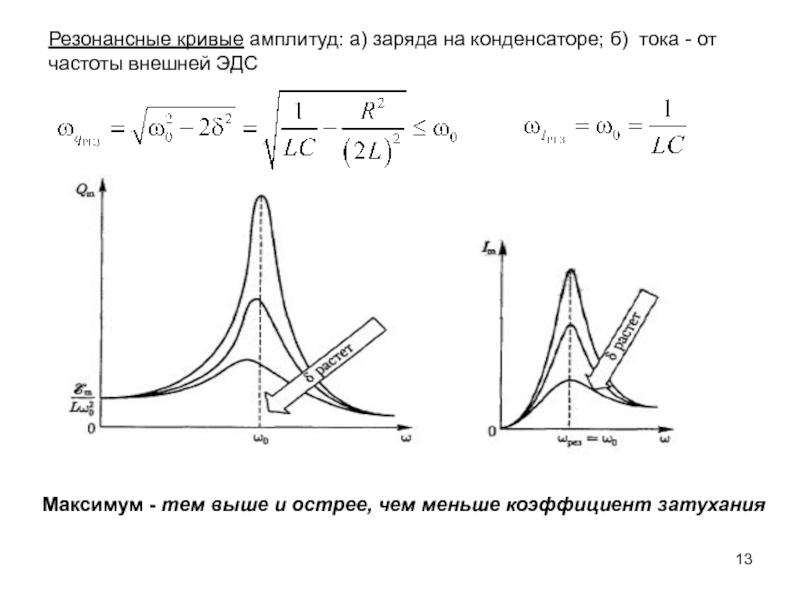
- 13. Резонансные кривые амплитуд: а) заряда на конденсаторе;
- 14. Переменный ток Переменным током называются вынужденные колебания
- 15. После интегрирования: Закон Ома:Напряжение UL
- 16. Закон Ома:Сила тока:- реактивное емкостное сопротивление Падение
- 17. Общий случай. Сумма мгновенных значений
- 18. Резонанс напряжений (последовательный резонанс): если из формулы
- 19. Резонанс токов (параллельный резонанс):наблюдается в цепи переменного
- 20. Если , то Явление резкого уменьшения амплитуды
- 21. Мощность, выделяемая в цепи переменного тока.Мгновенная мощность
- 22. Скачать презентанцию
Слайды и текст этой презентации
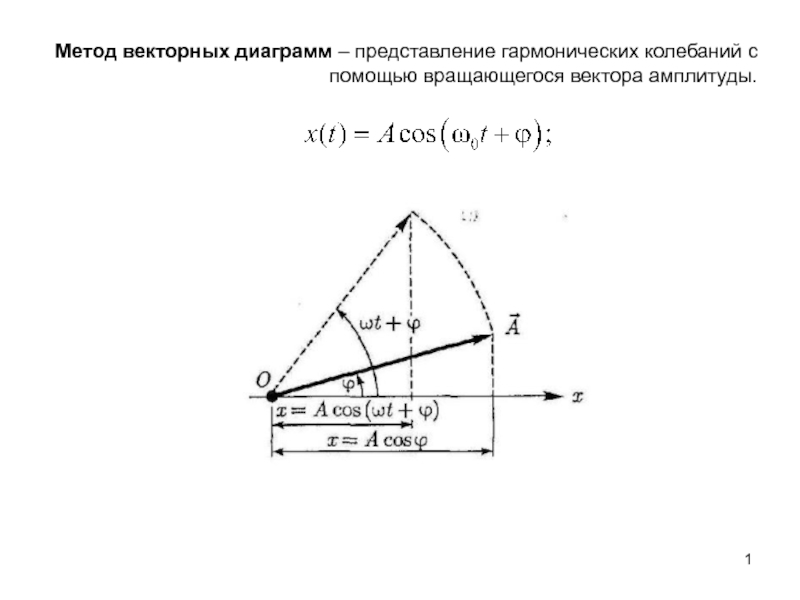
Слайд 1Метод векторных диаграмм – представление гармонических колебаний с помощью вращающегося
вектора амплитуды.
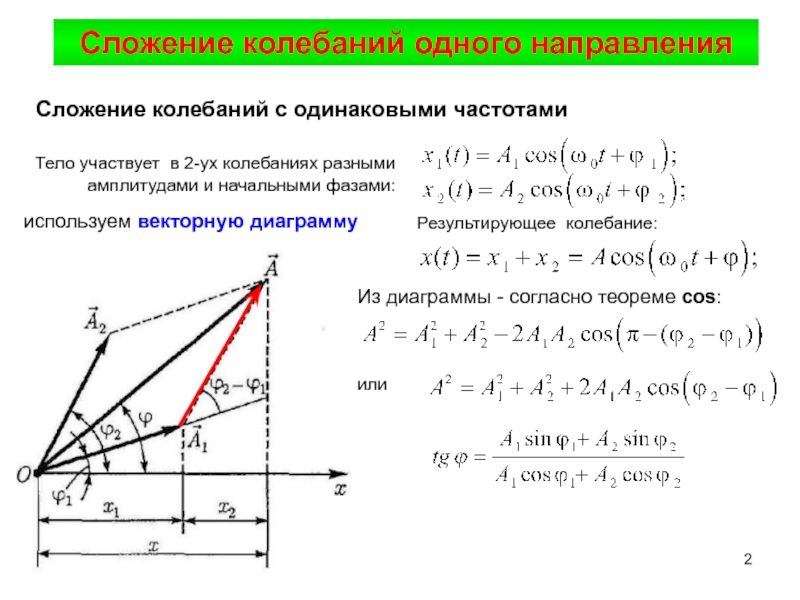
Слайд 2Сложение колебаний с одинаковыми частотами
Тело участвует в 2-ух колебаниях
разными амплитудами и начальными фазами:
Результирующее колебание:
Сложение колебаний одного направления
Из диаграммы
- согласно теореме cos:или
используем векторную диаграмму
Слайд 3б) Сложение колебаний с разными частотами и одинаковыми начальными фазами
:
Векторы амплитуд вращаются с разными угловыми скоростями угол между
векторами не постоянен изменяется и результирующая амплитуда А:Сумма этих и колебаний не является гармоническим колебанием.
в) Сложение колебаний с близкими частотами:
Результирующее колебание:
почти гармоническое со средней циклической
частотой и медленно меняющейся амплитудой:
используем сложение косинусов
Такие колебания называются биениями
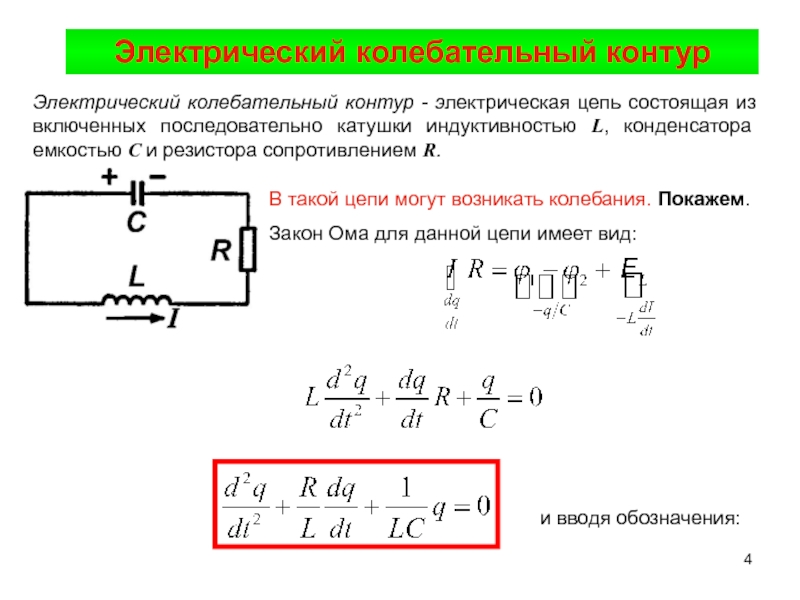
Слайд 4Электрический колебательный контур
Электрический колебательный контур - электрическая цепь состоящая из
включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора
сопротивлением R.В такой цепи могут возникать колебания. Покажем.
Закон Ома для данной цепи имеет вид:
и вводя обозначения:
Слайд 5При R = 0 - колебания незатухающие, при R
0 – колебания затухающие
дифференциальное уравнение свободных колебаний заряда
В
цепи с источником внешнего ЭДС закон Ома:или
Колебания вынужденные, если ЭДС изменяется по гармоническому закону
коэффициент затухания и собственная частота контура
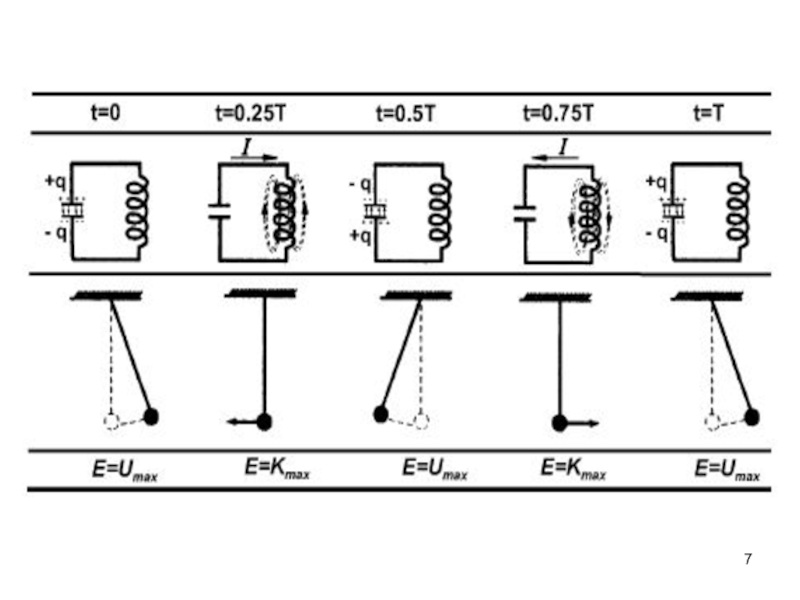
Слайд 6а) Свободные незатухающие колебания возникают в идеальном колебательном контуре при
R =0 и отсутствии внешнего источника, т.е.:
Полная энергия контура
складывается:из энергии конденсатора
(т.е. электрического поля) +
энергии катушки (т.е. магнитного поля) (см. контур).
Полная энергия математического маятника – сумма потенциальной и кинетической энергий:
Колебания обусловлены периодическим превращением энергий электрического и магнитного полей или изменением заряда q в конденсаторе и силы тока I в катушке .
Колебания обусловлены периодическим превращением потенциальной энергии в кинетическую.
Слайд 8Решение :
- амплитуда колебаний заряда;
Период колебаний:
- энергия электрического поля
конденсатора аналогична потенциальной энергии маятника,
- энергия магнитного поля катушки аналогична
кинетической энергии маятника,- сила тока в контуре аналогична скорости движения маятника.
- индуктивность L выполняет функцию массы.
- циклическая частота колебаний.
!!! сила тока в контуре опережает по фазе колебания заряда на 900.
Слайд 9Напряжение на конденсаторе по определению :
- волновое сопротивление колебательного контура.
Отношение
напряжения к силе тока – сопротивление:
поэтому:
Энергия электрического поля конденсатора:
Энергия
магнитного поля катушки индуктивности:Поскольку энергия электрического поля преобразуется в энергию магнитного поля - колебания в контуре называют электромагнитными колебаниями.
Слайд 10б) Свободные затухающие колебания : R 0.
.
Решение уравнения
при
где
постоянные, определяемые из начальных условий.
Уравнение:
происходит апериодический разряд конденсатора
Сопротивление,
при котором наступает этот процесс (знаменатель стремится к нулю) называется критическим:Слайд 11Сравнение характеристик колебательных процессов
пружинного маятника и колебательного контура
Слайд 12в) Вынужденные электрические затухающие колебания: если
или
Решение :
разность фаз между
колебаниями заряда и внешней ЭДС:
Сдвиг по фазе между током
и ЭДС :ток отстает от ЭДС при
ток опережает ЭДС при
Колебания заряда на С
Слайд 13Резонансные кривые амплитуд: а) заряда на конденсаторе; б) тока -
от частоты внешней ЭДС
Максимум - тем выше и острее, чем
меньше коэффициент затуханияСлайд 14Переменный ток
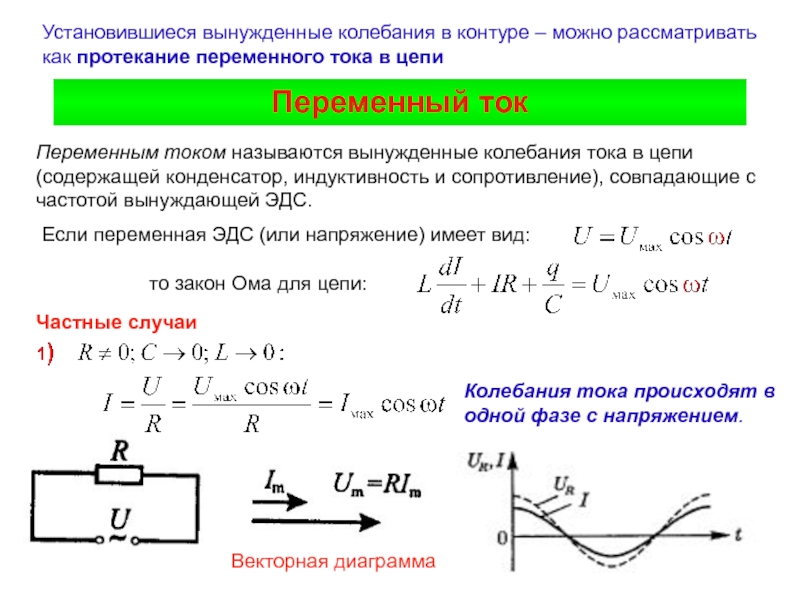
Переменным током называются вынужденные колебания тока в цепи
(содержащей конденсатор, индуктивность и сопротивление), совпадающие с частотой вынуждающей ЭДС.
то
закон Ома для цепи:Установившиеся вынужденные колебания в контуре – можно рассматривать как протекание переменного тока в цепи
Если переменная ЭДС (или напряжение) имеет вид:
Частные случаи
Колебания тока происходят в одной фазе с напряжением.
Векторная диаграмма
Слайд 15После интегрирования:
Закон Ома:
Напряжение UL опережает по фазе
ток I , текущий через катушку, на /2.
реактивное индуктивное сопротивление
Для постоянного тока (=0) катушка индуктивности не имеет сопротивления.
Падение напряжения на катушке:
Слайд 16Закон Ома:
Сила тока:
- реактивное емкостное сопротивление
Падение напряжения на конденсаторе:
Падение
напряжения UС отстает по фазе от текущего через
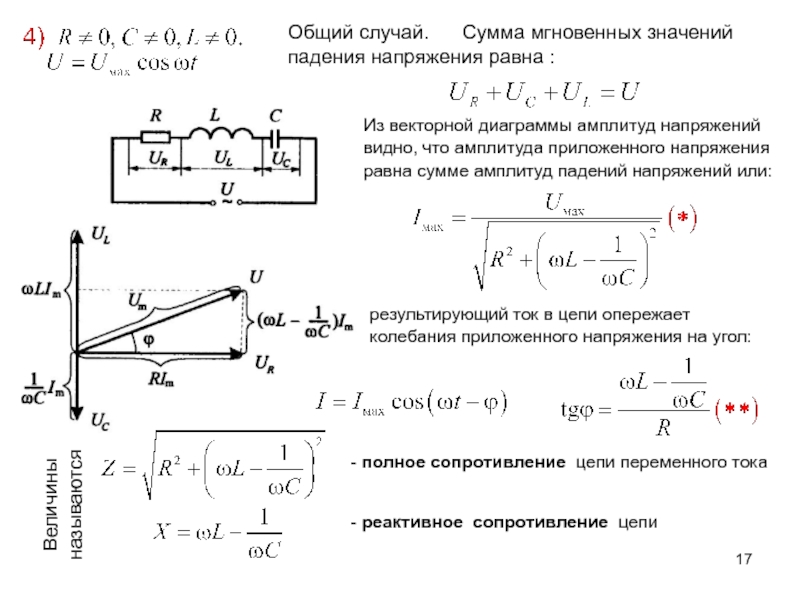
конденсатор тока I на /2.Слайд 17Общий случай. Сумма мгновенных значений падения напряжения равна
:
Из векторной диаграммы амплитуд напряжений видно, что амплитуда приложенного напряжения
равна сумме амплитуд падений напряжений или: результирующий ток в цепи опережает колебания приложенного напряжения на угол:
- полное сопротивление цепи переменного тока
Величины называются
- реактивное сопротивление цепи
Слайд 18Резонанс напряжений (последовательный резонанс): если
из формулы (**) следует,
что = 0 - изменения тока и напряжение происходят
синфазно;Z = R – ток определяется только активным сопротивлением и достигает максимального значения;
падение напряжения на конденсаторе UC и на катушке индуктивности UL одинаковы по амплитуде и противоположны по фазе.
- называется резонансной частотой.
Частота:
Векторная диаграмма случае резонанса напряжений и:
- добротность контура.
Отсюда следует - напряжения на реактивных сопротивлениях могут по амплитуде значительно превышать напряжение, приложенное к цепи.
Слайд 19Резонанс токов (параллельный резонанс):
наблюдается в цепи переменного тока, содержащей параллельно
включенные конденсатор и катушку индуктивности, к которой приложено напряжение:
а) участок 1С2 (R=0; L=0)
б) участок 1L2
Упрощение - активное сопротивление в обоих ветвях пренебрежимо мало
используя формулы (*) и (**)
(R=0; С=0)
Разность фаз токов в ветвях 1С2 и 1L2 равна а-б=, т.е. токи противоположны по фазе.
Амплитуда силы тока во внешней (неразветвленной) цепи:
Слайд 20Если
, то
Явление резкого уменьшения амплитуды силы тока во
внешней цепи, питающей параллельно включенные конденсатор и катушку индуктивности, при
приближении частоты приложенного напряжения к резонансной частоте называется резонансом токов (параллельным резонансом).В реальных цепях R0, то разность фаз , следовательно, Iмах0, но тем не менее амплитуда силы тока будет иметь наименьшее возможное значение.
Т.е., при резонансе токов во внешней цепи токи компенсируются и сила тока в подводящих проводах достигает минимального значения, обусловленного только током через резистор.
могут значительно превышать силу тока:
При резонансе токов силы токов:
Действующее или эффективное значение переменного тока:
Аналогично, действующее значение напряжения:
Слайд 21Мощность, выделяемая в цепи переменного тока.
Мгновенная мощность тока в цепи:
Практический
интерес представляет среднее за период значение мощности - активная мощность:
cos
- коэффициент мощности.Если в цепи отсутствует реактивное сопротивление (X = 0), то cos = 1 и
P = IU.
Если цепь содержит только реактивное сопротивление (R = 0), то cos = 0 и
P = 0, какими бы большими ни были ток и напряжение.