Слайд 15.4 Закономерности
случайной погрешности
Случайная погрешность является следствием ОДНОВРЕМЕННОГО влияния большого числа
разнородных, известных и неизвестных, зависимых и независимых СЛАБО ДЕЙСТВУЮЩИХ факторов.
Случайные
погрешности (СП) непостоянны по абсолютному значению и знаку и НЕ могут быть устранены введением поправки.
Случайную погрешность можно резко ослабить математической обработкой путем усреднения многократных неодновременных измерений или ряда одновременных наблюдений при неизменных условиях проведения измерения: .
СХОДИМОСТЬ измерений – это качество измерения, отражающее близость друг к другу результатов наблюдений, выполняемых в одинаковых условиях.
Слайд 25.4.1 Постулаты
случайной погрешности
(постулаты Гаусса)
Случайные погрешности одинаковые по величине, но противоположные
по знаку встречаются одинаково часто (равновероятны).
Случайные погрешности меньшие по величине
(модулю) встречаются чаще, чем большие.
Слайд 3Следствия:
а) Среднее арифметическое значение СП равно нулю при количестве измерений
стремящемся к бесконечности:
Т.к. , то математическое ожидание случайной погрешности равно нулю.
При
бесконечном числе опытов случайные погрешности взаимно компенсируют друг друга.
Слайд 4б) плотность распределения вероятности СП f(x), является чётной функцией аргумента,
а именно: f ( x ) = f ( –x ).
в)
плотность распределения вероятности СП f(x), является убывающей функцией модуля аргумента x:
f ’ (x) < 0, при x>0;
f ’ (x) > 0, при x<0;
f ’ (x) = 0, при х=0.
г) Центр распределения СП (максимум функции) находится в нуле.
Слайд 5Используя постулаты
и принимая во внимание, что
измерения без погрешности невозможно;
случайные
погрешности являются событиями независимыми. Все результаты измерений взаимно независимы;
число
измерений очень велико и все измерения выполняются равноточно;
Гаусс вывел НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ плотности вероятности случайных погрешностей.
Слайд 6
Математическое ожидание:
Дисперсия:
СКО: Мода распределения:
Слайд 7 Влияние D[x]
на вид графика
нормального закона
распределения.
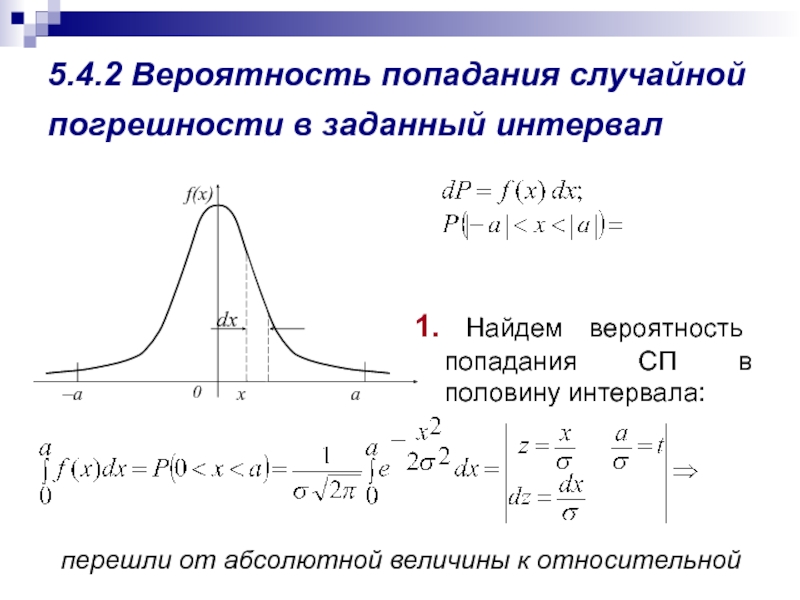
Слайд 85.4.2 Вероятность попадания случайной погрешности в заданный интервал
1. Найдем
вероятность попадания СП в половину интервала:
перешли от абсолютной величины
к относительной
Слайд 9
интеграл вероятности (интеграл Фурье, функция Лапласа).
Свойства интеграла Фурье
-
площадь фигуры, опирающейся на нулевое основание равна 0.
-
функция нечетная. Докажем:
Слайд 10Нормированная функция Лапласа:
2. Найдем вероятность попадания СП в полный интервал:
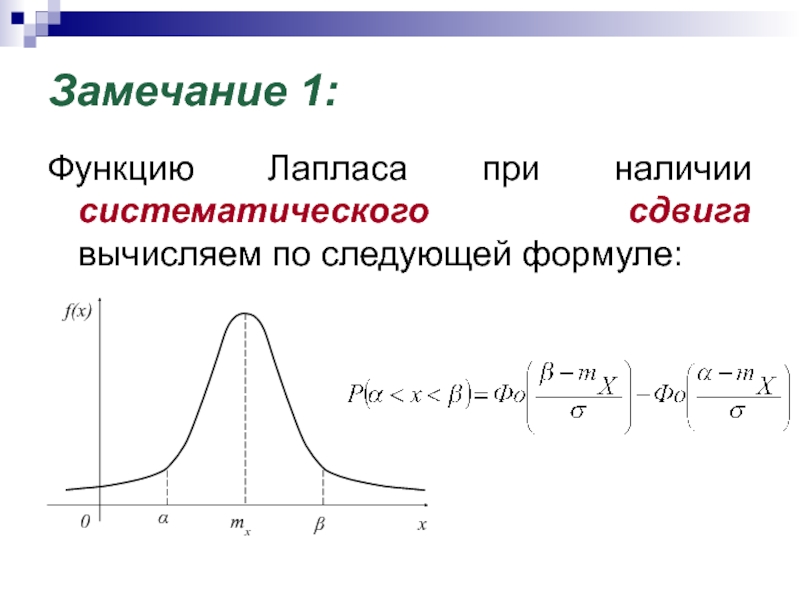
Слайд 12Замечание 1:
Функцию Лапласа при наличии систематического сдвига вычисляем по следующей
формуле:
Слайд 14Замечание 3:
Результирующая погрешность часто складывается из ряда составляющих с различными
плотностями распределения:
В связи с этим возникает задача нахождения суммарного закона
распределения погрешности.
Для суммы: , независимых непрерывных случайных величин, имеющих распределения , суммарный закон распределения погрешности называется композицией.
Слайд 155.4.3 Определение доверительных границ погрешностей СИ
МИНИМАЛЬНАЯ ШИРИНА ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА
обеспечивается при расположении последнего СИММЕТРИЧНО В ОБЕ СТОРОНЫ ОТ МАТЕМАТИЧЕСКОГО
ОЖИДАНИЯ.
Слайд 16
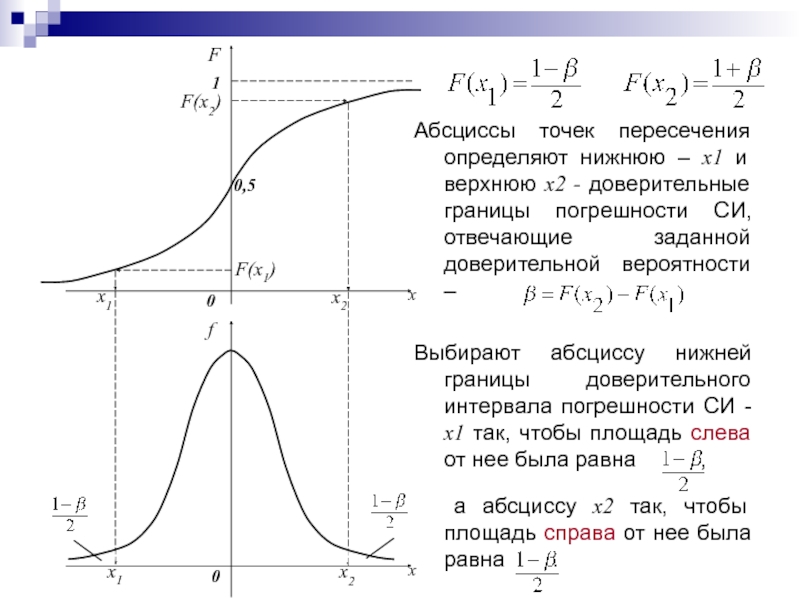
Абсциссы точек пересечения определяют нижнюю – x1 и верхнюю x2
- доверительные границы погрешности СИ, отвечающие заданной доверительной вероятности –
Выбирают
абсциссу нижней границы доверительного интервала погрешности СИ - x1 так, чтобы площадь слева от нее была равна ,
а абсциссу x2 так, чтобы площадь справа от нее была равна .
Слайд 17АЛГОРИТМ построения доверительного интервала случайной погрешности
определить точечную оценку математического ожидания
– , и СКО –
, случайной погрешности;
выбрать уровень доверительной вероятности – , из рекомендуемого ряда значений 0,90; 0,95; 0,99.
найти верхнюю – xв, и нижнюю – хн, границы доверительного интервала в соответствии с уравнениями
Значения xв и хн определяются из таблиц значений функции Лапласа.
Полученный доверительный интервал удовлетворяет условию:
где n – число результатов наблюдений;
t – аргумент функции Лапласа, отвечающий вероятности /2.
Слайд 18Пример: Проведено 50 измерений постоянного сопротивления. Определить доверительный интервал для
мат. ожидания истинного значения постоянного сопротивления, если закон распределения результатов
наблюдений нормальный с параметрами:
Ом;
Ом;
уровень доверительной вероятности принять =0,9.
Слайд 19Решение:
Так как гипотеза о нормальном виде закона распределения результатов наблюдения
не противоречит опытным данным, доверительный интервал определим по выражению:
Из таблицы
находим: t=1,65. Следовательно:
Ответ: 569 Ом < R < 611 Ом






![5. 4 Закономерности случайной погрешности Влияние D[x] на вид графика нормального закона распределения. Влияние D[x] на вид графика нормального закона распределения.](/img/thumbs/124898ab058cf74a0e3ab3f60076c5a2-800x.jpg)