Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 3 Применение методов линейного программирования в экономических моделях
Содержание
- 1. Лекция 3 Применение методов линейного программирования в экономических моделях
- 2. Учебные вопросы:Метод искусственного базисаЗадача об оптимальном распределении ресурсовДвойственная задача линейного программирования
- 3. Особенности задач линейного программированияЗадача о диете (о
- 4. Формулировка задачи о диете (рационе, смесях) в
- 5. Формулировка задачи об использовании ресурсов (планирования производства)
- 6. Формулировка задачи об использовании мощностей (о загрузке
- 7. Формулировка задачи о раскрое (распиле, обработке) в
- 8. Задача об использовании ресурсов (планирования производства)Для изготовления
- 9. Формализация задачи:Целевая функция:… Прибыль от производства единицы
- 10. Графическое решение задачи об использовании ресурсов4312
- 11. Способ определения первоначального допустимого базисного решения.Правило перехода
- 12. Теорема о разрешимости задачи ЛП.Если для системы
- 13. Полагаем неосновные переменные (x1 и x2) равными
- 14. Правила выбора разрешающего столбца и разрешающей строкиРазрешающий
- 15. 18/316/15/1∞Переход к следующей таблицей осуществляется по правилам:В
- 16. В результате получается следующее базисное решение: x
- 17. Аналогично находим следующее базисное решение, эффективность последовательно возросла с 0, затем 15, сейчас – 21. 5/5
- 18. Критерий оптимальности выполнен (в нижней строке нет
- 19. Слайд 19
- 20. Рассмотрим следующий примерРешить симплекс-методом задачу:При ограничениях:Пробуем решить
- 21. Метод искусственного базисаСуть метода: В каждое уравнение,
- 22. Решение примера М-методом
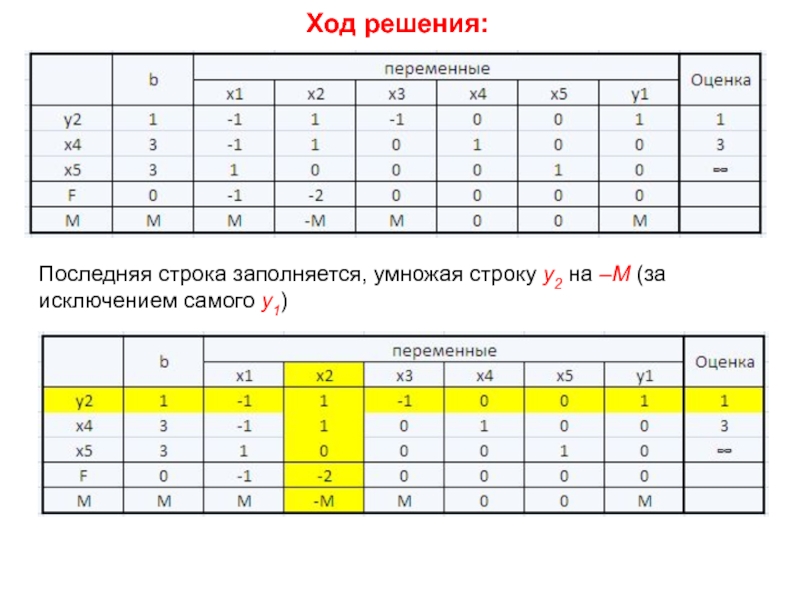
- 23. Ход решения:Последняя строка заполняется, умножая строку y2 на –М (за исключением самого y1)
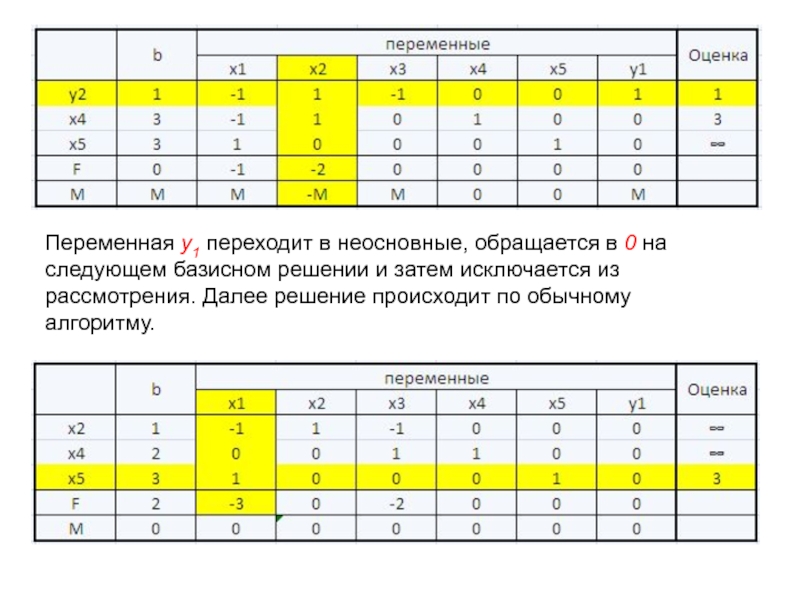
- 24. Переменная y1 переходит в неосновные, обращается в
- 25. Свойства двойственных задачВ прямой задаче ищут максимум
- 26. Две задачи ЛП, обладающие указанными свойствами, называются
- 27. Пример двойственной задачи:Уже известная Вам задача линейного программирования
- 28. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Учебные вопросы:
Метод искусственного базиса
Задача об оптимальном распределении ресурсов
Двойственная задача линейного
программирования
Слайд 3Особенности задач линейного программирования
Задача о диете (о рационе, о смесях);
Задача
об использовании ресурсов (планирования производства);
Задача об использовании мощностей (о загрузке
оборудования);Задача о раскрое материала.
Слайд 4Формулировка задачи о диете (рационе, смесях) в общем виде:
Составить дневной
рацион из n видов продуктов в количестве xj (j =
1, 2, …, n), стоимостью сj каждый. Содержание пищевых элементов i = 1, 2, …, m в дневном рационе должно быть не меньше bi. В единице каждого j–го продукта содержится aij единиц i-го пищевого элемента.Содержание пищевых элементов в рационе должно удовлетворять следующим условиям:
Целевая функция принимает максимальное значение:
Слайд 5Формулировка задачи об использовании ресурсов (планирования производства) в общем виде:
Найти
план выпуска n видов продукции с использованием m видов ресурсов.
где:
xj (j=1..n) – число единиц продукции каждого Pj типа, запланированного к производству.bi (i=1..m) – запас каждого вида ресурса Si;
aij – число единиц ресурса Si, затрачиваемого на изготовление единицы продукции Pj (технологические коэффициенты);
cj – прибыль от реализации единицы продукции вида Pj, удовлетворяющий условиям:
при котором целевая функция принимает максимальное значение:
Слайд 6Формулировка задачи об использовании мощностей (о загрузке оборудования) в общем
виде:
Предприятию дан план производства продукции по времени и номенклатуре: требуется
за время T выпустить n1, n2, …, nk единиц продукции P1, P2, …, Pk. Продукция производится на станках S1, S2, …, Sm. Для каждого станка известна производительность aij (число единиц продукции Pj, которое можно произвести на станке Si) и затраты bij на изготовление продукции Pj на станке Si в единицу времени.Найти план работы станков (распределить выпуск продукции между станками), чтобы затраты на производство всей продукции были минимальны.
Обозначим: xij – время, в течение которого станок Si будет занят изготовлением продукции Pj (i = 1, 2, …, m; j = 1, 2, …, k):
при котором целевая функция принимает минимальное значение:
Слайд 7Формулировка задачи о раскрое (распиле, обработке) в общем виде:
На раскрой
(распил, обработку) поступает материал одного образца в количестве a единиц.
Требуется изготовить из него y комплектующих изделий в количествах, пропорциональных числам b1, b2, …, by (условие комплектности). Каждая единица материала может быть раскроена n различными способами, в результате использования i-го способа (i = 1, 2, …, n) получается aik единиц k-го изделия (k = 1, 2, …, y).Необходимо найти план раскроя, обеспечивающий оптимальный план раскроя, обеспечивающий максимальное количество комплектов.
Обозначим через xi – число единиц материала, раскраиваемого i-тым способом. x – число изготавливаемых комплектов изделия. Тогда:
Целевая функция принимает максимальное значение:
Требование комплектности:
Очевидно:
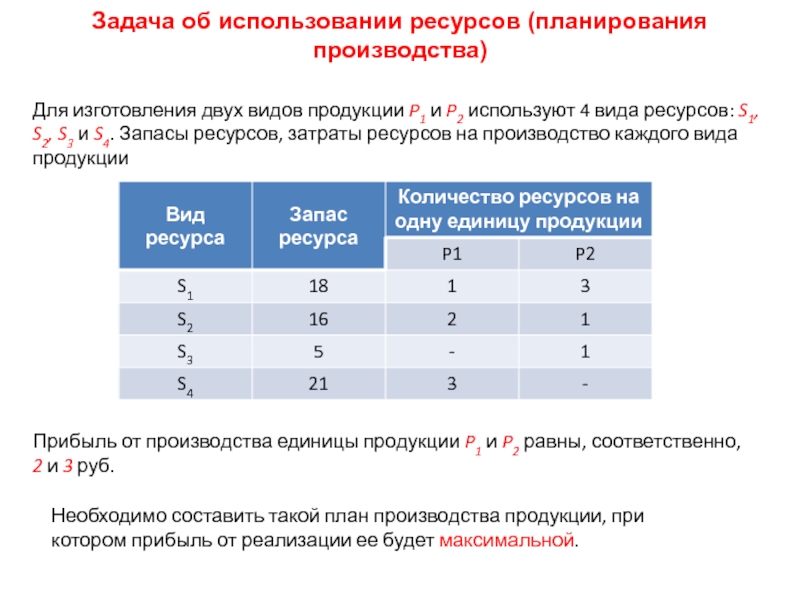
Слайд 8Задача об использовании ресурсов (планирования производства)
Для изготовления двух видов продукции
P1 и P2 используют 4 вида ресурсов: S1, S2, S3
и S4. Запасы ресурсов, затраты ресурсов на производство каждого вида продукцииПрибыль от производства единицы продукции P1 и P2 равны, соответственно, 2 и 3 руб.
Необходимо составить такой план производства продукции, при котором прибыль от реализации ее будет максимальной.
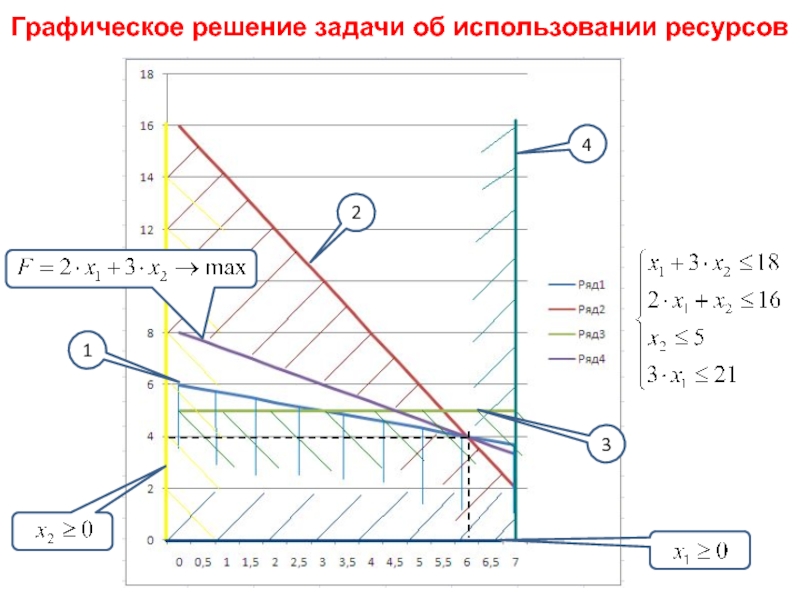
Слайд 9Формализация задачи:
Целевая функция:
… Прибыль от производства единицы продукции P1 и
P2 равны, соответственно, 2 и 3 руб. … и должна
стремиться к максимуму.План производства – количество единиц продукции P1 и P2 , которые обозначим x1 и x2. С учетом цены с1 = 2 и с2 = 3, целевая функция примет следующий вид:
Неравенства составляются по каждому ресурсу с подстановкой планируемого количества производства изделий каждого типа:
Не указанные явно в условии задачи, но очевидные условия на неотрицательность количества изделий каждого типа:
Слайд 11Способ определения первоначального допустимого базисного решения.
Правило перехода к лучшему (не
худшему) решению.
Критерий проверки оптимальности найденного решения.
Любые m переменных системы m
линейных уравнений с n переменными (m < n) называются основными (базисными) если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные n – m переменных называются неосновными (свободными).
Основными могут быть разные группы из n переменных.
Слайд 12Теорема о разрешимости задачи ЛП.
Если для системы m линейных уравнений
с n переменными (m < n) ранг матрицы коэффициентов при
переменных равен m, т.е. существует хотя бы одна группа основных переменных , то эта система называется неопределенной,причем каждому произвольному набору значений неосновных переменных соответствует одно решение системы.
Базисным решением системы m линейных уравнений с n переменными называется решение, в котором все n-m неосновных переменных равны нулю. Число базисных решений является конечным, т.к. оно равно числу групп основных переменных, не превосходящее Cnm
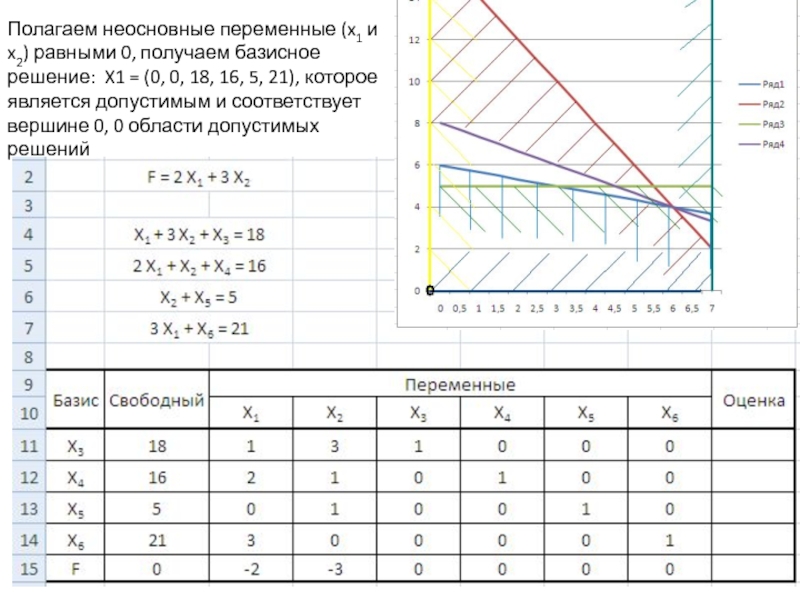
Слайд 13Полагаем неосновные переменные (x1 и x2) равными 0, получаем базисное
решение: X1 = (0, 0, 18, 16, 5, 21), которое
является допустимым и соответствует вершине 0, 0 области допустимых решенийСлайд 14Правила выбора разрешающего столбца и разрешающей строки
Разрешающий столбец определяет наибольший
(по модулю) отрицательный коэффициент Сj в нижней строке.
Разрешающая строка определяется
по минимальному соотношению, вычисляемого по следующим правилам:∞, если bi и aij имеют разные знаки.
∞, если bi = 0 и aij < 0.
∞, если aij = 0.
0, если bi = 0 и aij > 0.
| bi / aij |, если bi и aij имеют разные знаки.
На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент aij.
Теорема о допустимых базисных решениях
Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка многогранника решений, и наоборот, каждой угловой точке многогранника решений соответствует допустимое базисное решение.
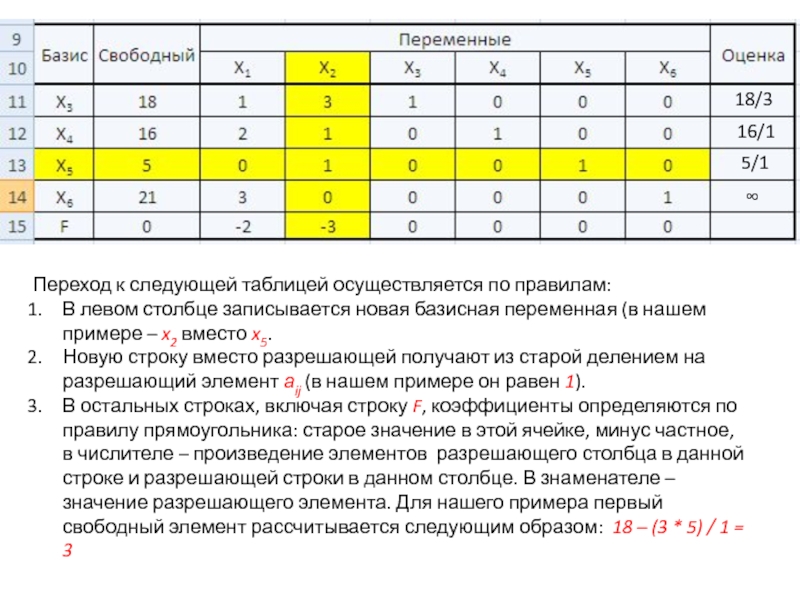
Слайд 1518/3
16/1
5/1
∞
Переход к следующей таблицей осуществляется по правилам:
В левом столбце записывается
новая базисная переменная (в нашем примере – x2 вместо x5.
Новую
строку вместо разрешающей получают из старой делением на разрешающий элемент aij (в нашем примере он равен 1).В остальных строках, включая строку F, коэффициенты определяются по правилу прямоугольника: старое значение в этой ячейке, минус частное, в числителе – произведение элементов разрешающего столбца в данной строке и разрешающей строки в данном столбце. В знаменателе – значение разрешающего элемента. Для нашего примера первый свободный элемент рассчитывается следующим образом: 18 – (3 * 5) / 1 = 3
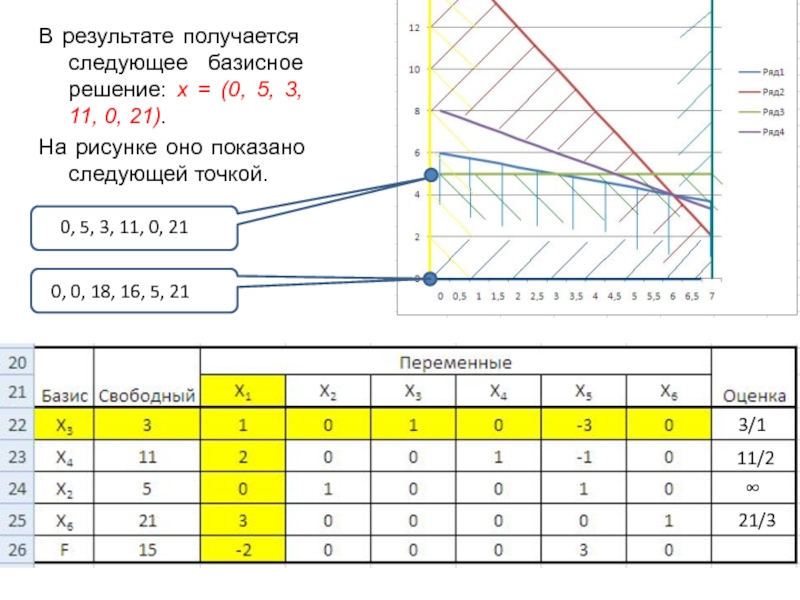
Слайд 16В результате получается следующее базисное решение: x = (0, 5,
3, 11, 0, 21).
На рисунке оно показано следующей точкой.
3/1
11/2
∞
21/3
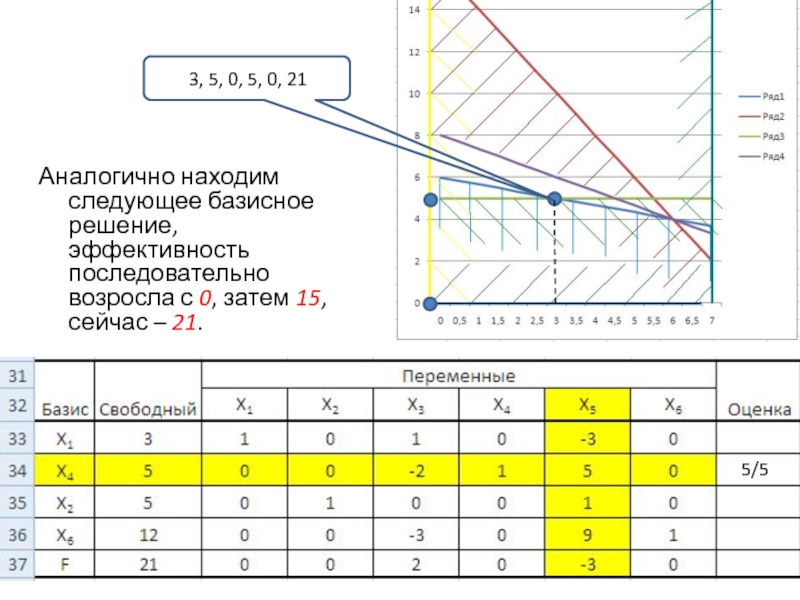
Слайд 17Аналогично находим следующее базисное решение, эффективность последовательно возросла с 0,
затем 15, сейчас – 21.
5/5
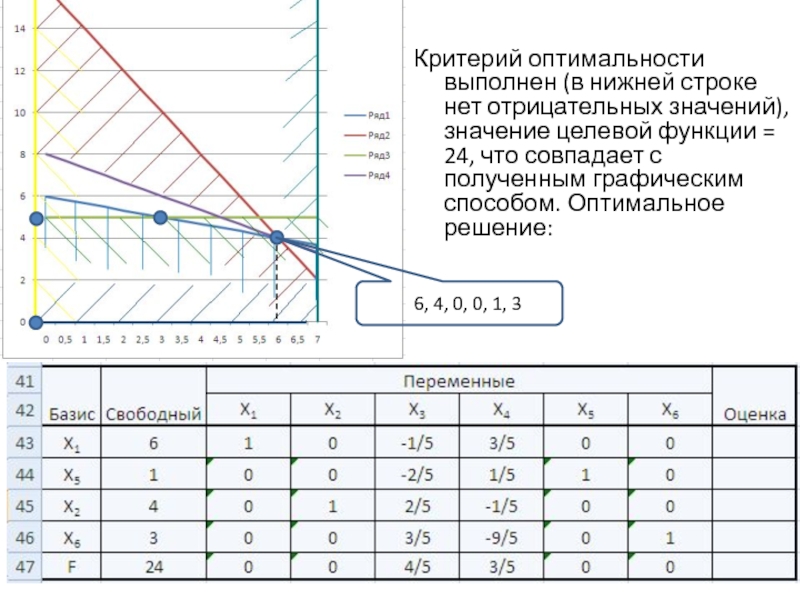
Слайд 18Критерий оптимальности выполнен (в нижней строке нет отрицательных значений), значение
целевой функции = 24, что совпадает с полученным графическим способом.
Оптимальное решение:Слайд 20Рассмотрим следующий пример
Решить симплекс-методом задачу:
При ограничениях:
Пробуем решить обычным симплекс –
методом:
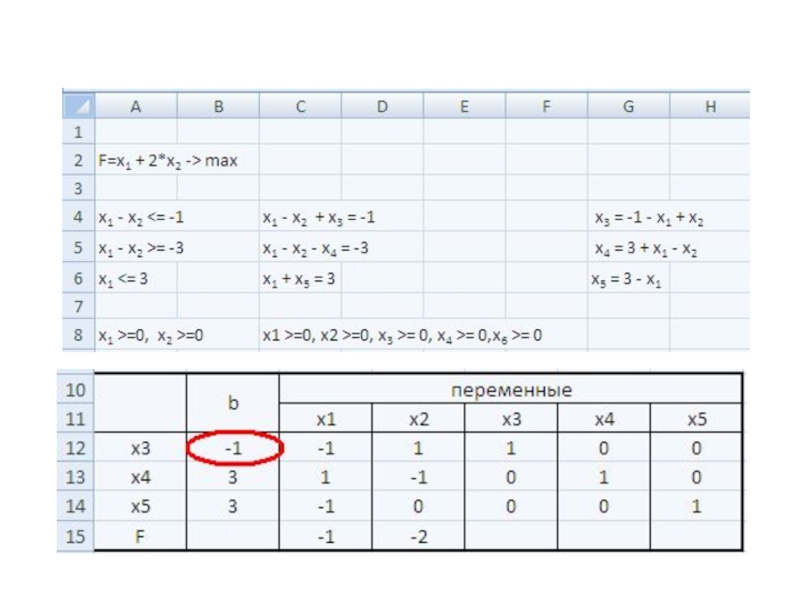
Даже не строя симплекс-таблицу, получаем первое базисное решение: X =
(0, 0, -1, 3, 3), которое недопустимо.Слайд 21Метод искусственного базиса
Суть метода:
В каждое уравнение, дающее отрицательную компоненту
в базисном решении вводим новую неотрицательную переменную y1, y2, …
yk, которая имеет тот же знак, что и свободный член в правой части уравнения.В симплекс-таблицу включаем и эти переменные.
Целевую функция заменяем функцией вида: T = F – M(y1 + y2 + … + yk), где М – произвольное большое число. Благодаря этому обозначению получил свое второе название: M- метод.
Тогда:
Если в оптимальном решении Т- задачи все искусственные переменные равны 0, то соответствующие значения остальных переменных дают оптимальное решение исходной задачи (т.е. Т = F при y1 = y2 = … = yk = 0, т.е. М = 0).
Если имеется оптимальное решение Т-задачи, при котором хотя бы одна из искусственных переменных отлична от 0, то система ограничений исходной задачи несовместна.
Если Т = ∞, то исходная задача также неразрешима, причем либо F = ∞, либо условия задачи противоречивы.
Слайд 23Ход решения:
Последняя строка заполняется, умножая строку y2 на –М (за
исключением самого y1)
Слайд 24Переменная y1 переходит в неосновные, обращается в 0 на следующем
базисном решении и затем исключается из рассмотрения. Далее решение происходит
по обычному алгоритму.Слайд 25Свойства двойственных задач
В прямой задаче ищут максимум функции, в двойственной
– минимум.
Коэффициенты при переменных в линейной (целевой) функции одной задачи
являются свободными членами системы ограничений в другой. Каждая из задач задана в стандартной форме, причем в задаче максимизации все неравенства вида <=, а в задаче минимизации все неравенства вида >=.
Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу.
Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.
Условия неотрицательности переменных имеются в обеих задачах.
Слайд 26Две задачи ЛП, обладающие указанными свойствами, называются симметричными взаимно двойственными
задачами, или просто двойственными задачами. Алгоритм составления двойственной задачи:
Привести все
неравенства системы ограничений исходной задачи к одному смыслу: если в исходной задаче ищут максимум целевой функции, то приводят их к виду: <=, если минимум, то к виду <=. Если требование не соблюдается, неравенство умножают на -1.Составить расширенную матрицу системы АI, в которую включить матрицу коэффициентов при переменных а, столбец свободных членов системы ограничений b и строку коэффициентов при переменных в целевой функции с.
Найти матрицу AII, транспонированную к АI.
Сформулировать двойственную задачу на основании полученной матрицы АI, и условия неотрицательности переменных.