Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы и приемы реализации математических моделей теплотехнических систем
Содержание
- 1. Методы и приемы реализации математических моделей теплотехнических систем
- 2. Анализ функциональной связи параметров математической модели Математическая
- 3. Формализованное описание структуры системыГрафическую структуру и связи
- 4. Технологическая схема ГТУ
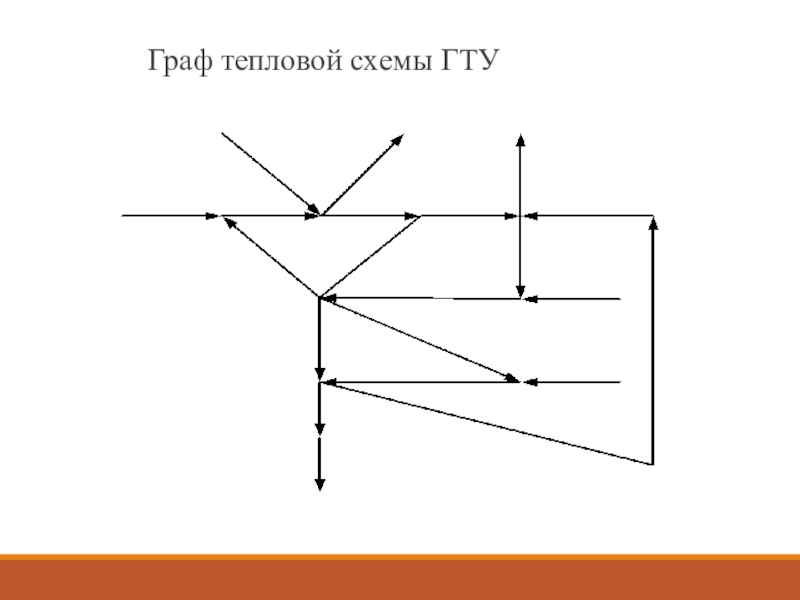
- 5. Граф тепловой схемы ГТУ
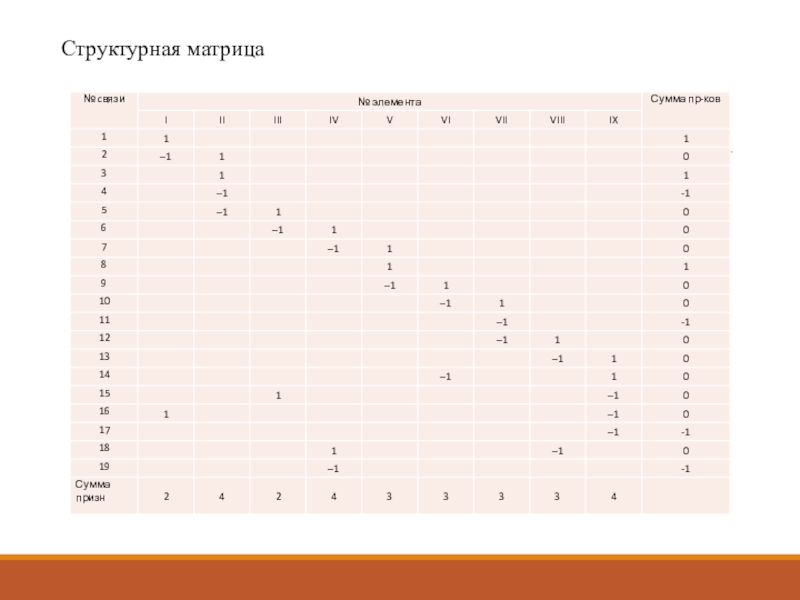
- 6. Структурная матрица
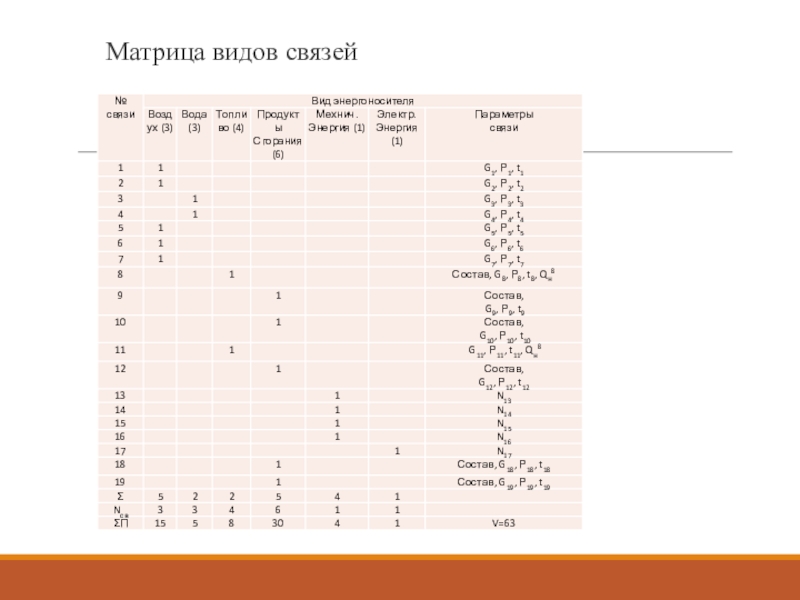
- 7. Матрица видов связей
- 8. Системы балансовых уравнений элементовбаланса энергии для k-го
- 9. В состав математической модели входит система балансовых
- 10. Все параметры, которые входят в систему балансовых
- 11. Согласно матрице функциональных связей для каждого n-го
- 12. Совокупность допустимого состава переменных для заданной технологической
- 13. Анализ данной матрицы позволяет определить состав неизвестных
- 14. Система ограничений на параметры Среди параметров и
- 15. Очевидно, что термодинамические, расходные и конструктивные параметры
- 16. Функция целиПри выполнении процедур анализа и оптимизации
- 17. Превышение числа параметров над числом уравнений означает,
- 18. Анализ СБУ и определение алгоритма ее расчетаДля
- 19. Сокращенная система балансовых уравненийG7+G8 – G9 = 0; G9+G11 – G12 = 0
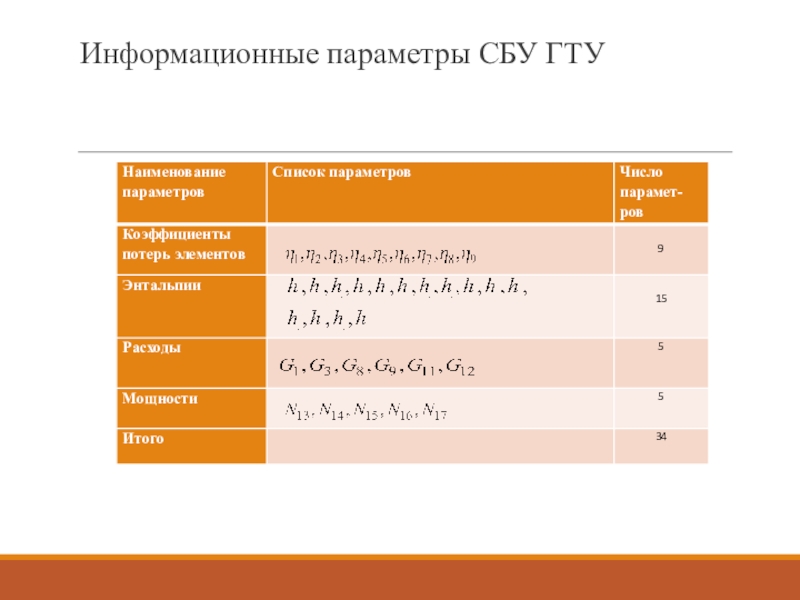
- 20. Информационные параметры СБУ ГТУ
- 21. Сокращенная матрица функциональных связей
- 22. Рассмотрим второй вариант – расчет на единицу
- 23. Слайд 23
- 24. Методика проведения процедуры параметрической оптимизации После определения
- 25. Алгоритм параметрической оптимизации в данном случае можно
- 26. Расчет тепловой технологической схемы заключается в нахождении
- 27. 3) комбинированный (интегрально-модульный ) расчет.Это расчет интегральный
- 28. СПАСИБО ЗА ВНИМАНИЕ!Минск, 2020 год
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Скачать презентанцию
Анализ функциональной связи параметров математической модели Математическая модель объекта макроуровне представляет собой совокупностьформализованного описания структуры системы, системы балансовых уравнений (СБУ), системы ограничений на параметры и характеристики теплотехнической системы;функции цели.
Слайды и текст этой презентации
Слайд 1Методы и приемы реализации математических моделей теплотехнических систем макроуровня
ИЮНЬ 2020
г.
Слайд 2Анализ функциональной связи параметров математической модели
Математическая модель объекта макроуровне представляет
собой совокупность
формализованного описания структуры системы,
системы балансовых уравнений (СБУ),
системы
ограничений на параметры и характеристики теплотехнической системы;функции цели.
Слайд 3Формализованное описание структуры системы
Графическую структуру и связи элементов в модели
можно представить с помощью графа.
После построения графа выполняется его
кодирование с использованием структурной матрицы и матрицы видов связей.Слайд 8Системы балансовых уравнений элементов
баланса энергии для k-го элемента;
материального баланса для
i-го энергоносителя в k-м элементе;
изменения энтальпии i-го энергоносителя в k-м
элементе;изменения давления i-го энергоносителя в k-м элементе.
Слайд 9
В состав математической модели входит система балансовых уравнений, число которых,
как правило, значительно меньше числа параметров системы.
Однако для заданной
производительности, известных конструктивных параметров и определение части термодинамических и расходных параметров системы, избыточных по отношению к числу уравнений, расчет системы балансовых уравнений дает однозначное действительное решение. Поэтому в отличие от ручных методов расчета, когда расчет тепловой или технологической схемы производятся отдельно, в случае автоматизации процесса моделирования производится совместный расчет тепловой или технологической схемы с техническими расчетами элементов системы. При этом производится уточнение показателей основного и вспомогательного оборудования, расхода теплоносителей и их пар-ров.
Слайд 10Все параметры, которые входят в систему балансовых уравнений называют информационными,
и их разделяют на 2 группы:
1 – независимые переменные.
2 –
зависимые переменные.Число последних должно быть равно числу уравнений в системе.
Понятие зависимое или независимое переменное носит условных характер. В зависимости от постановки задачи одна и та же переменная может быть как зависимая, так и независимая.
Например: мощность установки задана, тогда расход топлива определяется из расчета и является зависимой переменной. Если задан расход топлива, то мощность становиться зависимой переменной и, следовательно, находится из расчета.
Слайд 11Согласно матрице функциональных связей для каждого n-го уравнения k-го элемента
системы оставляется, по крайней мере, один такой зависимый параметр yNk,
определяемый из этого уравнения, который не может быть найден из уравнения балансов для соседнего элемента. Это обеспечивает совместимость уравнений по отдельным элементам и в целом по теплотехнической системе. Это означает также техническую возможность создания данного варианта системы. При несовместимости заданной системы уравнений теплотехническая система технически неосуществима.Следовательно, чтобы решить СБУ необходимо определить все независимые переменные X. В случае выполнения параметрической оптимизации входные переменные делят на две группы: вектор независимых регламентируемых переменных L и вектор независимых управляемых (оптимизируемых) R
X =L + R.
Слайд 12Совокупность допустимого состава переменных для заданной технологической схемы определяется с
помощью матрицы функциональной связи, в которой единица в i-ой строках
матрицы дают логический признак наличия непосредственной связи j-ой переменной с одной или несколькими переменными входящими в i-ое уравнения сис-мы балансовых уравнений.Слайд 13Анализ данной матрицы позволяет определить состав неизвестных параметров. Таким образом,
чтобы для каждого уравнения системы задается один свой зависимый (неизвестный)
параметр, который в явном виде не может быть найден из уравнений для соседних элементов. Реализация такой возможности означает с одной стороны совместимость уравнений системы балансовых уравнений, а с другой стороны техническая возможность создания данного варианта схемы.После составления математической модели и анализа переменных можно переходить к процедурам анализа и оптимизации исследуемого варианта технологической схемы теплотехнической системы.
При этом процедура анализа (расчета) состоит из следующих этапов:
1) выбор допустимого сочетания значений независимых параметров;
2) расчет системы балансовых уравнений.
3) расчет функции цепи.
Слайд 14Система ограничений на параметры
Среди параметров и многочисленных технологических характеристик
отдельных элементов оборудования теплотехнической системы встречаются достаточно сложные зависимости различного
рода. Установление этих зависимостей является задачей совместного теплового, гидравлического, аэродинамического и прочностного расчетов элементов оборудования при их разработке.Кроме того, существуют ограничения на величины, являющиеся функциями параметров, например, скорость энергоносителей, температура конструктивных элементов.
Вместе с тем, анализ указанных зависимостей и их систематизация для различных видов элементов оборудования конкретного типа показывают, что все характеристики процессов и конструкций можно в конечном итоге выразить в явной форме или определить итерационно в зависимости от одной и той же совокупности параметров связей Z и конструктивных параметров установки Zk.
Слайд 15
Очевидно, что термодинамические, расходные и конструктивные параметры установки Z и
Zk не могут принимать совершенно произвольные значения. Они в состоянии
изменяться только в пределах физически возможных и технически осуществимых состояний энергоносителей и конструкций.Эти ограничения для различных элементов оборудования, материалов и энергоносителей обычно записывают в виде неравенств для указанных параметров.
Все указанные ограничения определяют в многомерном пространстве переменных Z и Zk некоторую область, называемую допустимой областью исследования.
Термодинамические, расходные и конструктивные параметры Z и Zk в процессе проектирования и оптимизации могут принимать лишь значения, которые находятся внутри или на границе допустимой области исследования (оптимизации).
Слайд 16Функция цели
При выполнении процедур анализа и оптимизации в качестве итогового
показателя эффективности сравниваемых вариантов системы рекомендуется принимать один или несколько
энергетических критериев эффективности.Задача оптимизации теплотехнической системы в этом случае конкретизируется следующим образом: найти значения параметров технологического процесса, состав элементов оборудования и вид технологической схемы, совокупности которых соответствуют максимуму (или минимуму) критерия эффективности.
Для вычисления выбранных критериев эффективности определяют функции цели. В наиболее общем случае критерий эффективности теплотехнической системы полностью определяется значениями термодинамических, расходных и конструктивных параметров, параметров, описывающих структуру системы, а также значениями внешних влияющих факторов.
Слайд 17Превышение числа параметров над числом уравнений означает, что система балансовых
уравнений имеет бесконечное множество решений. Таким образом, изменяя значение, параметров
можем получить целый ряд сбалансированных стационарных состояний теплоэнергетической системы. Отсюда вытекает возможность оптимизации значения параметров.Совокупность допустимого состава переменных для заданной технологической схемы определяется с помощью матрицы функциональной связи, которой единице в i-ой строках матрицы дают логический признак наличия непосредственной связи j-ой переменной с одной или несколькими переменными отброшенные i-ой уравнения системы.
Слайд 18Анализ СБУ и определение алгоритма ее расчета
Для анализа эффективности технологической
схемы на стадии технико-экономического обоснования выбора варианта технического решения достаточно
проанализировать сокращенную СБУ, состоящую только из уравнений энергетических и материальных балансов. При этом считаем, что нам известны зависимости или алгоритмы определения энтальпий теплоносителей и рабочих тел в виде функций от термодинамических параметров.Возвращаясь к нашему примеру мы получаем систему балансовых уравнений из 11 уравнений.
Слайд 22Рассмотрим второй вариант – расчет на единицу электрической мощности установки.
В этом случае расход воздуха становится величиной зависимой, а электрическая
мощность установки – регламентируемой. Сокращенный вариант матрицы функциональных связей тогда примет вид, приведенный в таблице ниже.Слайд 24Методика проведения процедуры параметрической оптимизации
После определения алгоритма решения системы
балансовых уравнений переходят к разработке программы параметрической оптимизации. Определяется область
исследования (оптимизации). Это делается путем введения ограничений на параметры математической модели. В целях экономии места при выполнении курсового проекта диапазоны допустимых изменений переменных представляются в таблице перечня параметров математической модели. Для проведения параметрической оптимизации следует определить критерий эффективности и записать функцию цели. Выбираем в качестве критерия эффективности коэффициент полезного действия установки . Функцию цели можно в этом случае записать в видеСлайд 25Алгоритм параметрической оптимизации в данном случае можно представить в виде
многовариантного анализа для локализации экстремального значения с последующим уточнением. Алгоритм
решения системы балансовых уравнений принят для варианта расчета на единицу расхода рабочего тела (воздуха). В качестве управляемых в численном эксперименте заданы начальная температура воздуха на входе в компрессор t1 и температуры продуктов сгорания на входе в газовую турбину t7 (t12 = t7). Соответственно для диапазонов изменения указанных переменных:t1min t1 t1mах;
t7min t7 t7mах.
Слайд 26Расчет тепловой технологической схемы заключается в нахождении точных значений параметров
всех потоков, а при необходимости и конструктивных пар-ров, которые удовлетворяют
как уравнения системы балансовых уравнений, так и моделям всех элементов, а так же системе ограничений на параметры.Различают 3 подхода к расчету технологической схемы:
1) интегральный метод (одновременный расчет всех неизвестных); Этот метод обычно применяется в том случае, если модели всех элементов либо линейные, либо могут быть приведены к квазилинейному виду.
2) последовательный (модульный) расчет;
Данный метод основан на использовании анализа структуры теплотехнической системы и представление модели ее элементов в виде зависимости между входными и выходными параметрами. Он заключается в последовательном, элемент за элементом расчете.
Методика расчета ТТС
(систем балансовых уравнений)
Слайд 273) комбинированный (интегрально-модульный ) расчет.
Это расчет интегральный расчет СБУ с
учетом стуктуры ТТС. В данном случае определяется оптимальная последовательность решений
уравнений исходя из анализа структуры технологической схемы.Для разомкнутых систем данный метод предпочтителен и, как правило, не вызывает трудностей для определения последовательности элемента.
Для большинства ТТС характерны схемы с множеством обратных связей, т.е. существование контуров. В этом случае для применения последовательного метода расчета необходимо выявить разомкнутую схему эквивалентную исходной замкнутой. Другими словами определить связи, по которым происходит разрыв контуров, после чего происходит итерациональный расчет методом последовательных приближений.