Пологие оболочки Полубезмоментная теория цилиндрических оболочек

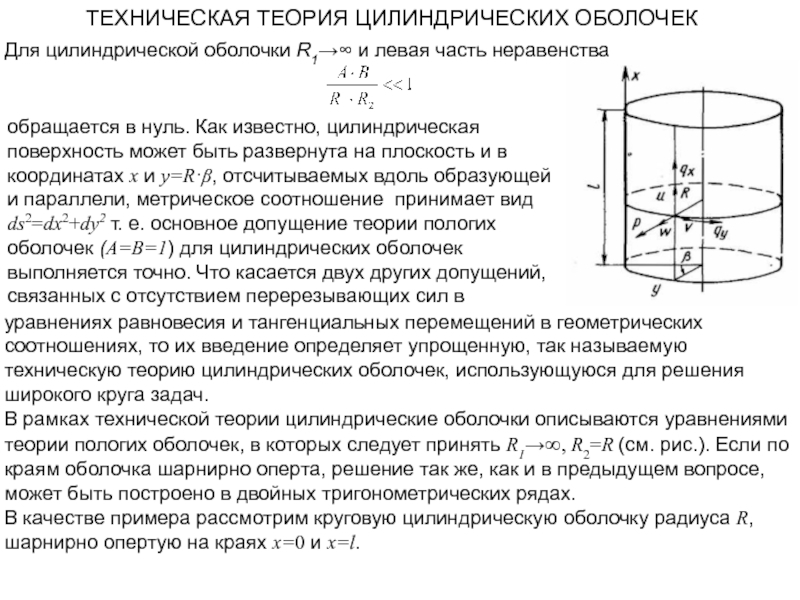
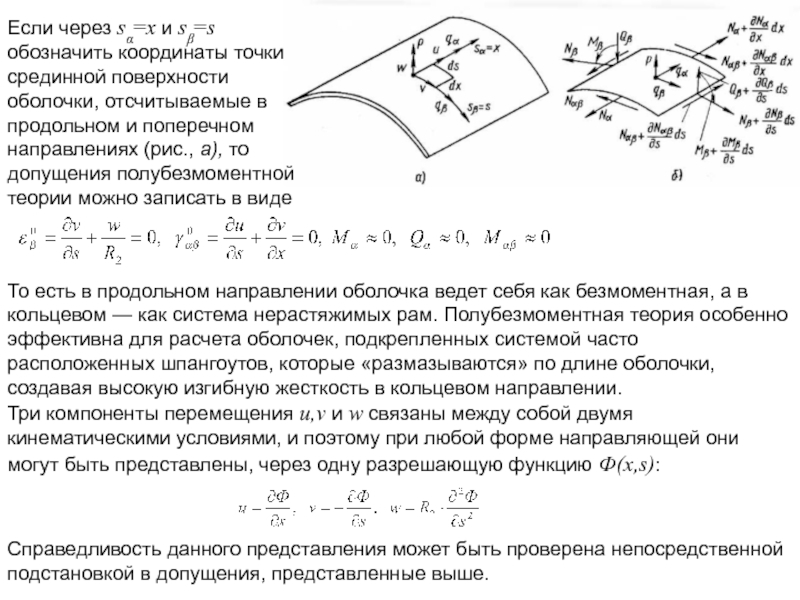
ввести некоторую систему криволинейных коор-динат, такую, что расстояние между дву-мя

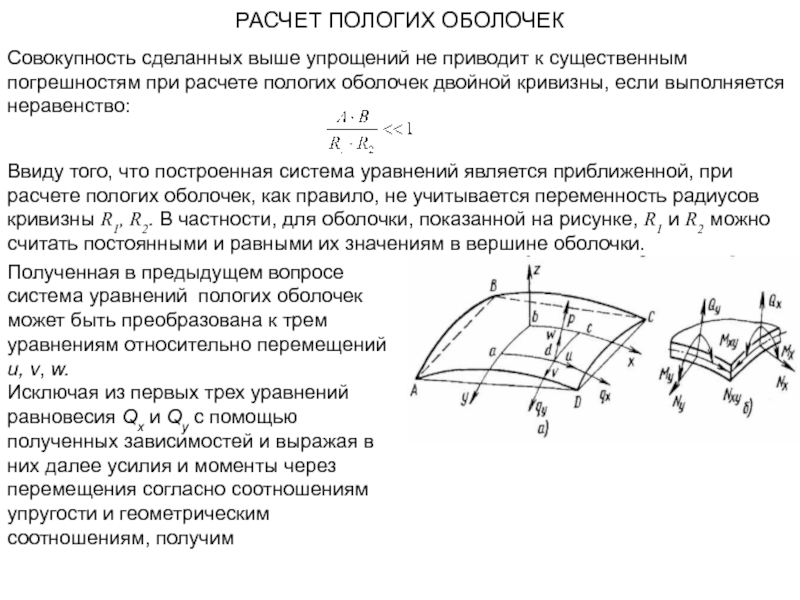
точками и угол между двумя направ-лениями на поверхности можно прибли-женно отождествить с расстояниями между точками и углами между линиями, лежащими на некоторой плоскости.

Типичная форма пологой оболочки или искривленной панели показана на рис.а. Криволинейный элемент abcd поверхности такой оболочки в координатах х, у можно приближенно отождествить с его проекцией на плоскость ABCD, а криволинейные координаты х, у — с декартовыми координатами.
Основное упрощение, вытекающее из этого предположения заключается в том, что метрическое соотношение общей теории в координатах х, у можно приближенно заменить следующим: , т. е. принять А=В=1.
Помимо этого, в теории пологих оболочек принимается, что при проектировании действующих на элемент сил на оси х и у можно в силу малой кривизны оболочки не учитывать составляющие от перерезывающих сил Qx и Qy (см. рис. б), а в геометрических соотношениях, определяющих изменения кривизн, учитывать только нормальное перемещение w.

Основные гипотезы и исходные соотношения

принимают вид
Соотношения упругости сохраняются без изменения:
Геометрические соотношения записываются в форме
где
Полученные

уравнения отличаются от соответствующих уравнений теории пластин наличием членов Nx/Rl, Ny/R2 во втором уравнении равновесия и членов w/R1, w/R2 в геометрических соотношениях для линейных деформаций.

уравнений равновесия имеем
С учетом приведенных зависимостей граничные условия записываются в

той же форме как и в общей теории оболочек.
Полученные уравнения в силу своей простоты по сравнению с уравнениями общей теории широко применяются для решения самых разнообразных задач по расчету оболочек. Остановимся на некоторых приложениях.

Обобщенные перерезывающие силы, используемые для записи граничных условий имеют вид

при расчете пологих оболочек, как правило, не учитывается переменность радиусов

кривизны R1, R2. В частности, для оболочки, показанной на рисунке, R1 и R2 можно считать постоянными и равными их значениям в вершине оболочки.

Совокупность сделанных выше упрощений не приводит к существенным погрешностям при расчете пологих оболочек двойной кривизны, если выполняется неравенство:

Полученная в предыдущем вопросе система уравнений пологих оболочек может быть преобразована к трем уравнениям относительно перемещений и, v, w.
Исключая из первых трех уравнений равновесия Qx и Qy с помощью полученных зависимостей и выражая в них далее усилия и моменты через перемещения согласно соотношениям упругости и геометрическим соотношениям, получим

qx=qy=0, система уравнений пологих оболочек может быть приведена к двум

уравнениям.
Введем функцию напряжений φ так, как это было сделано в теории пластин

где

Тогда первые два уравнения равновесия (при qx=qy=0) удовлетворяются тождественно, а третье уравнение равновесия после исключения Qx, Qy и замены Мх, Μy, Мху через w, a Nx, Ny — через φ примет вид

прогиба w и функции напряжений φ. Эти уравнения можно привести

к одному уравнению относительно w. Действуя бигармоническим оператором на уравнение первое уравнение и исключая с помощью второго уравнения, можно записать одно уравнение восьмого порядка

Используя выражения для деформаций и путем их дифференцирования исключая функции и и v, получим уpавнение совместности деформаций, аналогичное в теории пластин

Заменяя через Nx, Ny, Nxy с помощью соотношений упругости и вводя функцию напряжений φ, получим

(см. рис) решение может быть построено путем разложения искомых функций

в двойные тригонометрические ряды как в теме про расчет шарнирно опертых прямоугольных пластин.
Граничные условия в рассматриваемом случае записываются в следующем виде:

при x=0 и x=a: w=v=0, при y=0 и y=b: w=u=0,

Для того чтобы удовлетворить эти граничные условия, искомые функции w и φ достаточно представить рядами вида

где wmn, φmn — постоянные коэффициенты разложений, которые необходимо определить.
Представляя внешнюю нагрузку р(х, у) таким же рядом

где ртп — известные коэффициенты, и подставляя ряды для w и φ в два уравнения четвертого порядка, получим алгебраическую систему уравнений для определения wmn и φmn:

получим

w и р
в уравнение восьмого порядка. Полученный ряд

для прогиба оболочки w сходится значительно медленнее соответствующего разложения для пластины, так как первое слагаемое знаменателя, обеспечивающее его сходимость, содержит малый коэффициент D, пропорциональный h3.
В случае, когда граничные условия не соответствуют условиям шарнирного опирания, решение может быть получено методами, рассмотренными в теории пластин. Значение полученных уравнений не исчерпывается только возможностью расчета пологих оболочек. Теория пологих оболочек в силу простоты ее уравнений и достаточной точности в большинстве практических случаев находит также широкое применение при решении задач локальной деформации оболочек при действии сосредоточенных нагрузок и задач устойчивости оболочек, когда на ее поверхности образуются местные складки. Основанием для этого является то, что на относительно малом участке поверхности оболочка практически всегда может считаться пологой и соответствующее локальное напряженное состояние может быть описано полученными выше уравнениями.

неравенства


обращается в нуль. Как известно, цилиндрическая поверхность может быть

развернута на плоскость и в координатах х и у=R·β, отсчитываемых вдоль образующей и параллели, метрическое соотношение принимает вид ds2=dx2+dy2 т. е. основное допущение теории пологих оболочек (А=В=1) для цилиндрических оболочек выполняется точно. Что касается двух других допущений, связанных с отсутствием перерезывающих сил в

уравнениях равновесия и тангенциальных перемещений в геометрических соотношениях, то их введение определяет упрощенную, так называемую техническую теорию цилиндрических оболочек, использующуюся для решения широкого круга задач.
В рамках технической теории цилиндрические оболочки описываются уравнениями теории пологих оболочек, в которых следует принять R1→∞, R2=R (см. рис.). Если по краям оболочка шарнирно оперта, решение так же, как и в предыдущем вопросе, может быть построено в двойных тригонометрических рядах.
В качестве примера рассмотрим круговую цилиндрическую оболочку радиуса R, шарнирно опертую на краях х=0 и х=l.

нормальное давление р(х,β), распределенное симметрично относительно радиальной плоскости β=0, а

тангенциальные нагрузки отсутствуют (qx=qy=0)

Подставляя разложения u, v, w и р в полученные уравнения теории пологих оболочек








и приравнивая по отдельности члены левых и правых частей уравнений, содержащие одинаковые тригонометрические функции, для каждой тройки неизвестных коэффициентов итп, vmn, wmn получим по три линейных алгебраических уравнения:

от коэффициентов разложения нагрузки ртn.
Аналогичным образом решаются и уравнения







В

результате получается система из которой находятся wmn и φmn

назначения и методы расчета цилиндрических оболочек разработаны наиболее полно. Уравнения

теории цилиндрических оболочек могут быть получены из уравнений общей теории оболочек, если принять А=В=1, R1→∞, R2=R. Путем введения некоторых упрощающих предположений в предыдущем вопросе были получены уравнения технической теории цилиндрических оболочек. Преобразуем уравнение

для цилиндрической оболочки, на которую не действуют поверхностные нагрузки, т. е. qx=qy=р=0 (см. рис.). При R1→∞ и R2=R уравнение принимает вид

ОСНОВНЫЕ ГИПОТЕЗЫ И ИСХОДНЫЕ СООТНОШЕНИЯ

В случае шарнирного опирания по краям решение этого уравнения может быть получено в виде двойного тригонометрического ряда типа

периодичности по окружной координате у может быть представлено, в виде
Подставляя

данный ряд в решаемое уравнеие и приравнивая нулю коэффициенты при cos(ny/R), получим для wn(x) обыкновенное дифференциальное Уравнение восьмого порядка

Решение данного уравнения содержащее восемь произвольных постоянных Cin для каждого n, позволяет удовлетворить любые граничные условия на краях х=0 и х=l. Однако практическое определение частных решений Fni(x) уравнения восьмого порядка связано с большими трудностями, что и вызывает потребность в дальнейшем упрощении теории для снижения порядка уравнения.
Именно такой упрощенной теорией и является рассматриваемая в данном вопросе полубезмоментная теория цилиндрических оболочек, широко используемая при решении конкретных задач, в частности, для расчета цилиндрических оболочек средней длины, нагруженных таким образом, что их деформированное состояние меняется медленно в продольном направлении. В этой теории наряду с гипотезами Кирхгофа используются дополнительные упрощающие статические и кинематические допущения.

оболочки, отсчитываемые в продольном и поперечном направлениях (рис., а), то

допущения полубезмоментной теории можно записать в виде

То есть в продольном направлении оболочка ведет себя как безмоментная, а в кольцевом — как система нерастяжимых рам. Полубезмоментная теория особенно эффективна для расчета оболочек, подкрепленных системой часто расположенных шпангоутов, которые «размазываются» по длине оболочки, создавая высокую изгибную жесткость в кольцевом направлении.
Три компоненты перемещения и,v и w связаны между собой двумя кинематическими условиями, и поэтому при любой форме направляющей они могут быть представлены, через одну разрешающую функцию Ф(x,s):

Справедливость данного представления может быть проверена непосредственной подстановкой в допущения, представленные выше.

в силу сделанного выше замечания о возможности применения полубезмоментной теории

для расчета оболочек, подкрепленных шпангоутами, введены различные обозначения для жесткостей Eα·h и Dβ. При этом в полубезмоментной теории влиянием коэффициента Пуассона пренебрегают, полагая μ=0. Сдвигающее усилие (поток касательных напряжений) в срединной поверхности оболочки определяется из уравнения равновесия в продольном направлении:

Уравнение для неизвестной функции Ф можно получить с помощью вариационного принципа Лагранжа.

иметь вид
Вариация работы поверхностных нагрузок определяется равенством
Подставляя полученные выражения

в уравнение δU-δA=0 и преобразуя его интегрированием по частям таким образом, чтобы под поверхностным интегралом в качестве общего множителя была вариация δФ, получим дифференциальное уравнение для функции Ф и естественные граничные условия.

R2=R=const и х=R·α, s=R·β (см. рис.). После интегрирования по частям

интегралов уравнения δU-δA=0 по α и β с учетом периодичности Ф и ее производных в окружном направлении получим

где , l — длина оболочки.
Отсюда следует дифференциальное уравнение для функции Ф, которое запишем в виде

где

быть заданы перемещения (тогда δи=0, δν=0) или должны быть равны

нулю соответствующие им усилия Να=0, Nαβ=0. Поверхностные нагрузки, действующие на круговую цилиндрическую оболочку, могут быть представлены в форме тригонометрического ряда по окружной координате β. Например, при нагрузках, симметричных относительно образующей β=0, правая часть дифференциального уравнения для Ф может быть записана в виде ряда

Разрешающая функция Φ(α,β) в этом случае находится в виде ряда

На торцах полубезмоментной оболочки граничные условия формулируются так же, как и для безмоментной оболочки — на каждом торце должны быть заданы или тангенциальные перемещения, или соответствующие им тангенциальные усилия, т. е. и или Nα, v или Nαβ. Аналогичный результат следует и из вариационного уравнения. Контурный интеграл представляет вариацию работы реакций на торцах; он может быть записан в виде

где Фn(α) — неизвестные функции.

При этом в случае n=0, представляющем осесимметричное напряженно-деформированное состояние, полубезмоментная

теория неприменима (так как εβ=0) и это состояние рассчитывается отдельно по безмоментной теории с учетом краевых эффектов. Для первой гармоники (n=1), представляющей изгиб оболочки как балки, полубезмоментная теория не учитывает сдвиг (γαβ=0), и поэтому более точное решение можно получить на основе общей безмоментной теории (здесь также можно учесть краевые эффекты изгиба).
Для каждой последующей гармоники (n=2,3,...) получим обыкновенное дифференциальное уравнение

где

Полученное уравнение в отличие от уравнения пологой оболочки имеет уже четвертый порядок и по виду совпадает с уравнением осесимметричного краевого эффекта. Его решение можно записать в аналогичной форме

где — частное решение неоднородного уравнения.

величине и при небольших значениях

n является достаточно малым. Вследствие этого деформированное состояние тонкой оболочки при малых n меняется вдоль образующей медленно. В этом случае удобнее решение записать через функции А. Н. Крылова:

Они делятся на симметричные (К1 и К3) и антисимметричные (К2 и К4) относительно х=0 и их производные выражаются через эти же функции в виде:

Функции А. Н. Крылова имеют вид :

Произвольные постоянные Ci или Ai определяются из четырех граничных условий на торцах оболочки. В случае необходимости решение, полученное по полубезмоментной теории, при не слишком больших n может быть дополнено решением в виде осесимметричного краевого эффекта.
Полубезмоментная теория применима для расчета деформаций, медленно изменяющихся вдоль образующей; для гладкой оболочки это ограничение определяется неравенством .