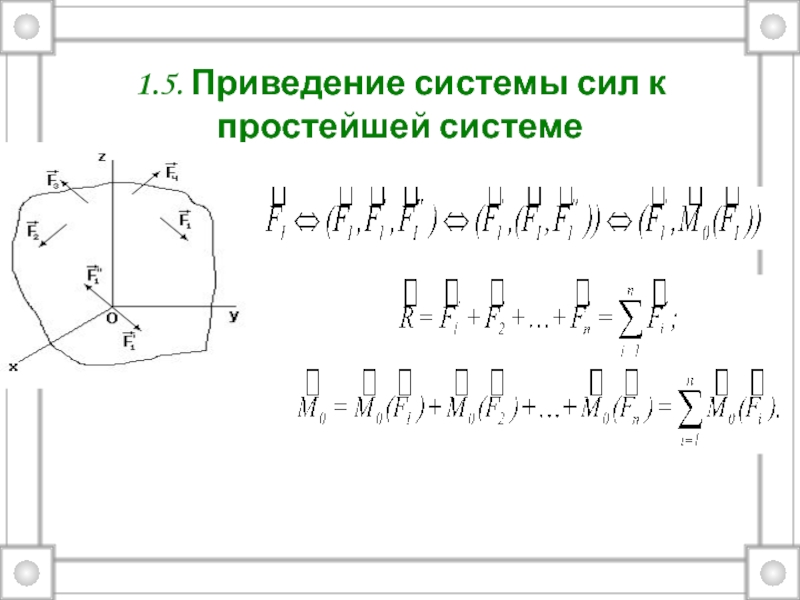
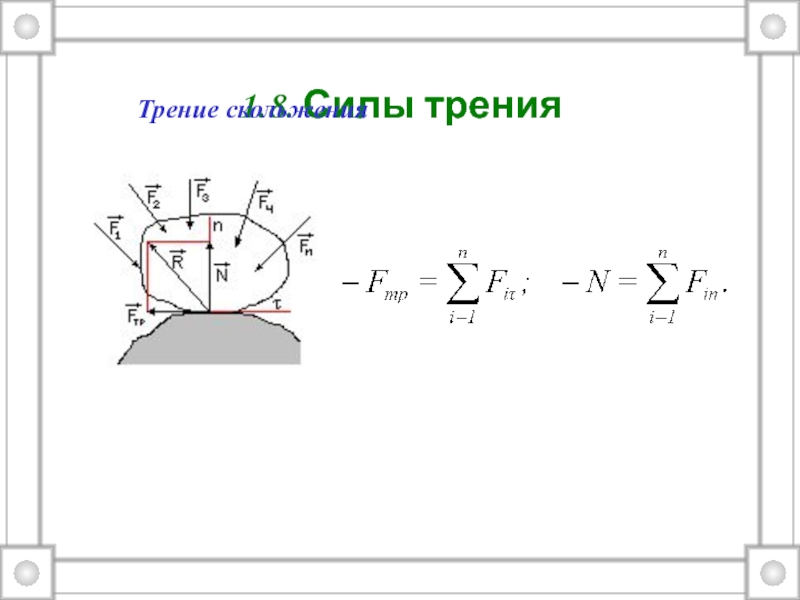
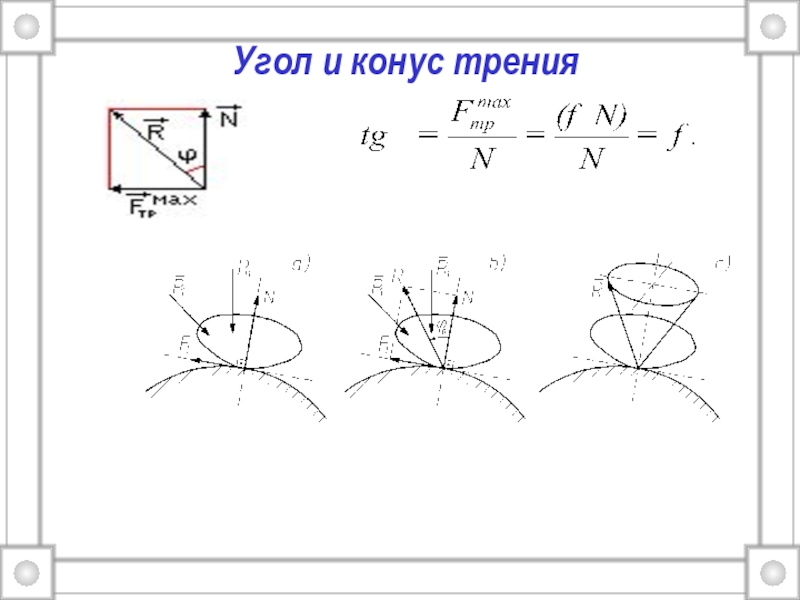
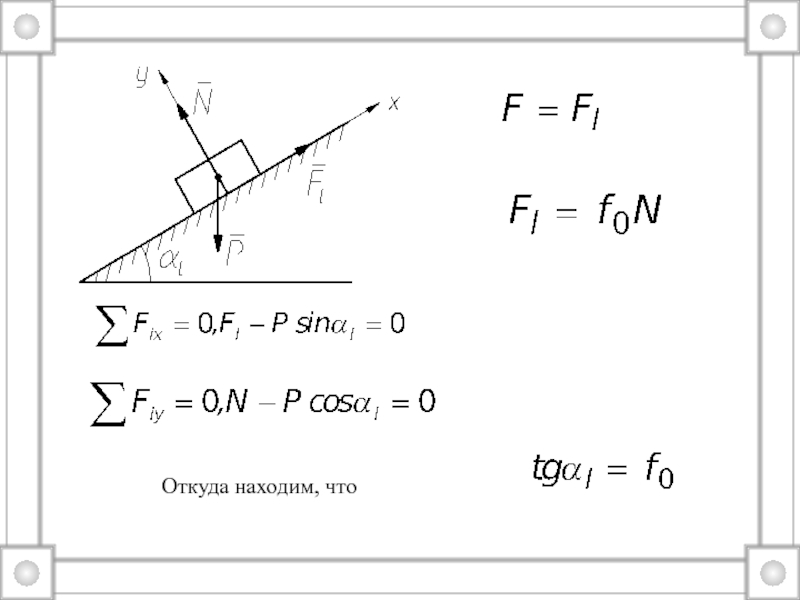
только одним свойством – массой.
Механическая система – любая совокупность материальных
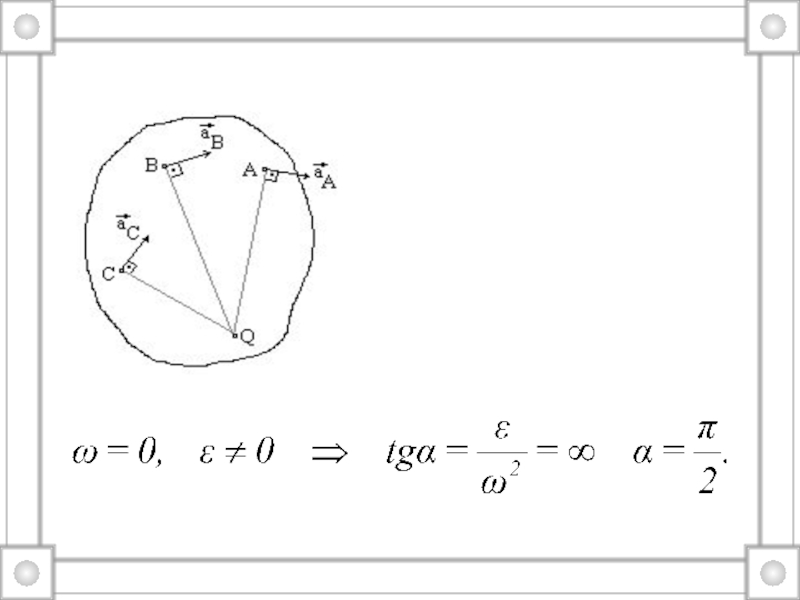
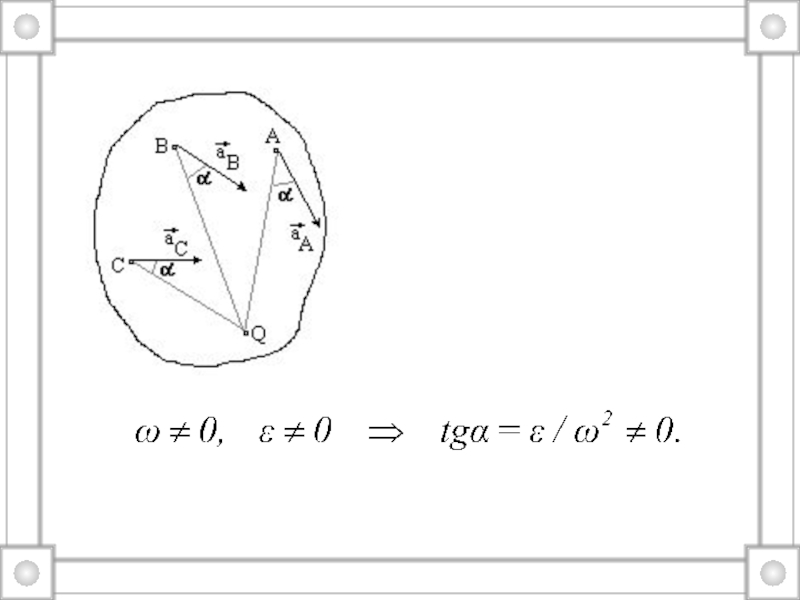
точек.Абсолютно твердое тело – механическая система, расстояние между точками которой не изменяется при любых взаимодействиях.
Силой называют одну из векторных мер механического действия одного материального объекта на другой. Сила характеризуется модулем, точкой приложения, линией действия, следовательно, является величиной векторной.
Система сил – любая совокупность сил. Системы сил, оказывающие одинаковое действие на твердое тело, называются эквивалентными. Система сил, эквивалентная нулю, не изменяет состояния тела (механической системы) и называется уравновешенной.