Задачи линейного программирования

изучающее методы решения экстремальных (оптимизационных) задач, которые характеризуются линейной зависимостью

между переменными и линейным показателем эффективности.

Критерий эффективности операции (функция цели) - линейная функция нескольких переменных
f (х1, х2,…, хn)= с1х1+ с2х2 + …+ сnхn ;

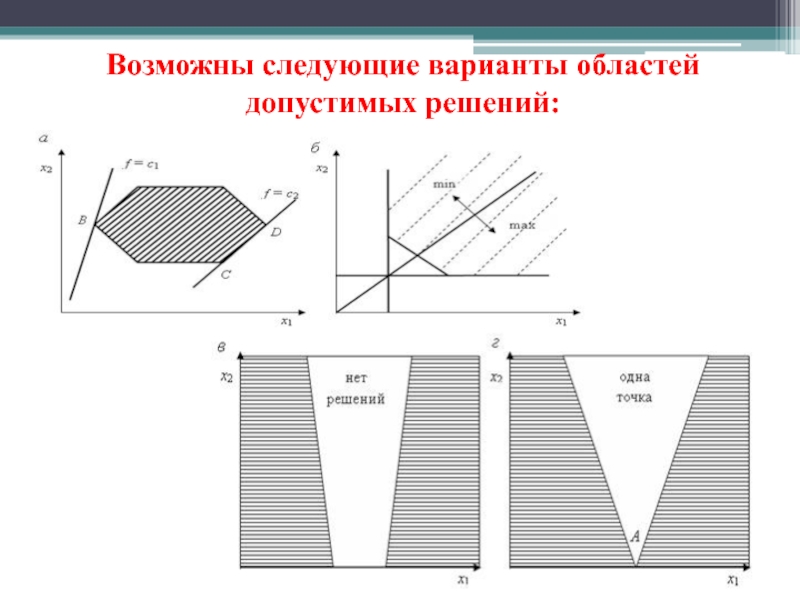
Условия, которыми должны обладать переменные, определяют некоторую область G, задаваемую системой линейных равенств и/или неравенств (система ограничений).

следующим образом: необходимо найти такое решение системы ограничений, удовлетворяющее дополнительным

условиям, при котором целевая функция достигает своего оптимального (максимального или минимального решения)

 

 

виде системы линейных уравнений.
При этом переменные задачи х1, х2, ..., хn являются

неотрицательными:

 

 

виде системы линейных неравенств.
При этом переменные задачи х1, х2, ..., хn являются

неотрицательными:

 

 

как всякое равенство в системе ограничений равносильно системе взаимно противоположных

неравенств.
С помощью введения дополнительных переменных задачу стандартной формы можно преобразовать в задачу канонического вида.
Путем изменения знака целевой функции задачу на максимум можно преобразовать в задачу на минимум и наоборот.

 

 

 

источников массовой информации: телевидения, радио, Internet и печатной продукции .
Анализ

рекламной деятельности в прошлом показал, что эти средства приводят к увеличению прибыли соответственно на 10, 5, 7 и 4 усл. ед., в расчете на 1 усл. ед., затраченную на рекламу. На рекламу выделено 50 000 усл. ед. Администрация предприятия не намерена тратить на телевидение более 40 %, а на радио и Internet— более 50 % от общей суммы выделенных средств. Как следует предприятию организовать рекламу, чтобы получить максимальную прибыль?

рекламы товара.

Управляющие переменные:
х1 – количество средств, вложенных в рекламу на телевидение;
х2 – количество

средств, вложенных в рекламу на радио;
х3 – количество средств, вложенных в рекламу в Internet;
х4 – количество средств, вложенных в рекламу в виде печатной продукции

средств, предусмотренных на рекламу по телевидению, на радио и в

Internet, и условия неотрицательности управляющих переменных.
Критерий оптимальности (целевая функция) выражает величину суммарной прибыли, зависящей от использования рекламы разного вида

Область допустимых решений (ОДР) имеет вид:

 

 

20000; 5000; 0) дает оптимальное значение целевой функции 395 000

у.е.
То есть, для получения максимальной прибыли в размере 395 000 усл. ед. надо распределить средства на рекламу следующим образом: 
20 000 усл. ед. вложить в рекламу на телевидении;
20 000 усл. ед. вложить в рекламу в Internet;
5000 усл. ед. вложить в рекламу, организованную с помощью печатной продукции;
рекламу на радио организовывать не следует.

такой форме может быть сведена и каноническая задача (с ограничениями

в виде уравнений), когда число переменных n больше числа уравнений m на 2

системой ограничений
Алгоритм графического решения ЗЛП

к прямой с1х1+с2х2 = F)

Алгоритм графического решения ЗЛП

целевой функции
Алгоритм графического решения ЗЛП

входа» и «точку выхода» (первая встретившаяся опорной прямой точка из

ОДР и последняя встретившаяся опорной прямой точка из ОДР соответственно) В точке входа: F  min В точке выхода: F  max

Алгоритм графического решения ЗЛП

и найти значение целевой функции в ней
Алгоритм графического решения ЗЛП
Замечание:
Оптимальная

точка является угловой точкой выпуклой области допустимых решений

F(B) Максимальное значение: Fmax = 
Частные случаи

F(E) Максимальное значение целевая функция достигает во всех точках отрезка ВС

: Fmin = F(B)= F(C)

Частные случаи

опорную прямую

и определяем «точку выхода»
В – точка выхода

и (3)

уравнений: