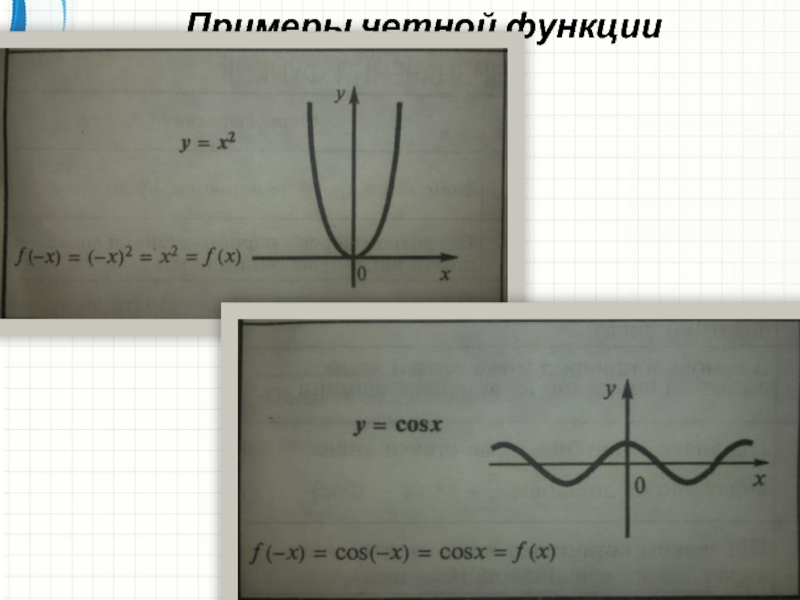
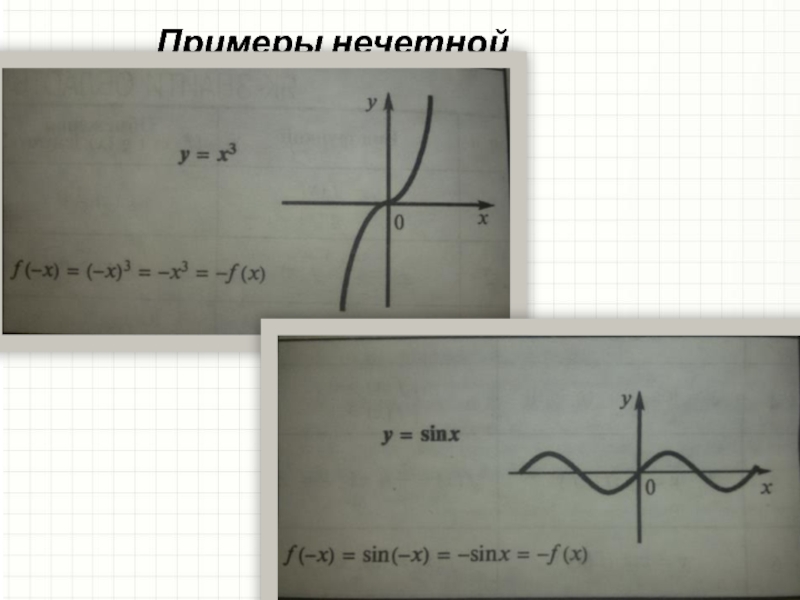
непрерывность, четность/нечётность.
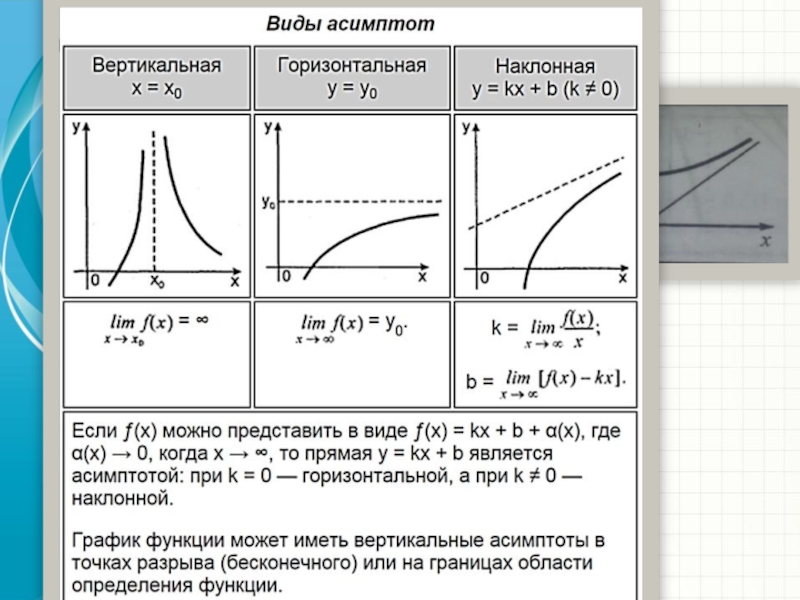
2) Асимптоты графика функции.
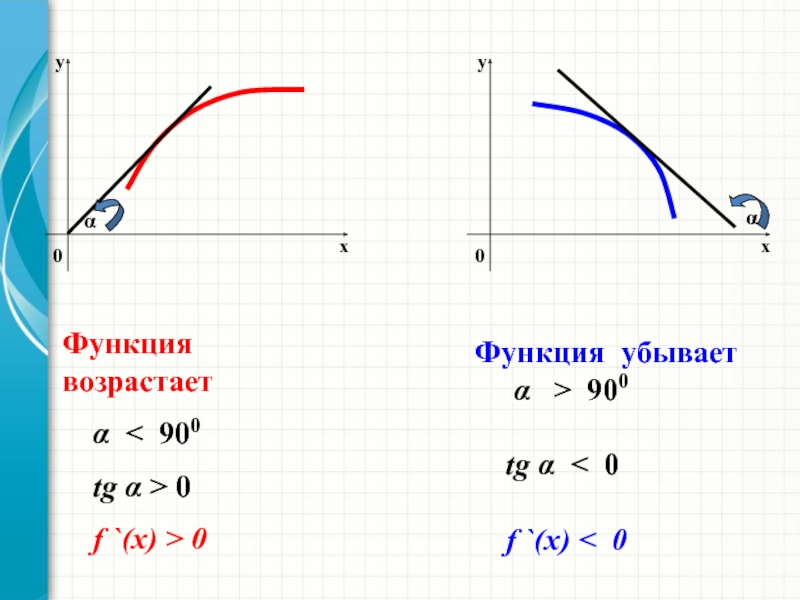
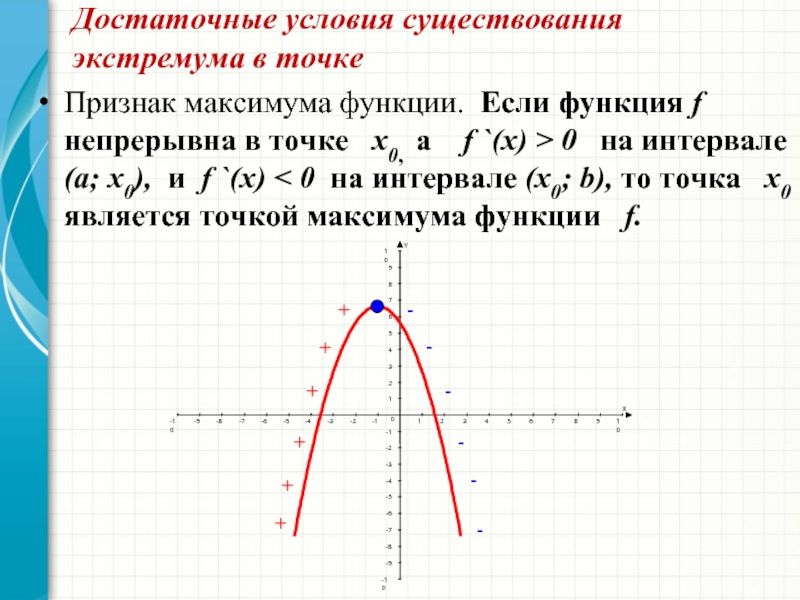
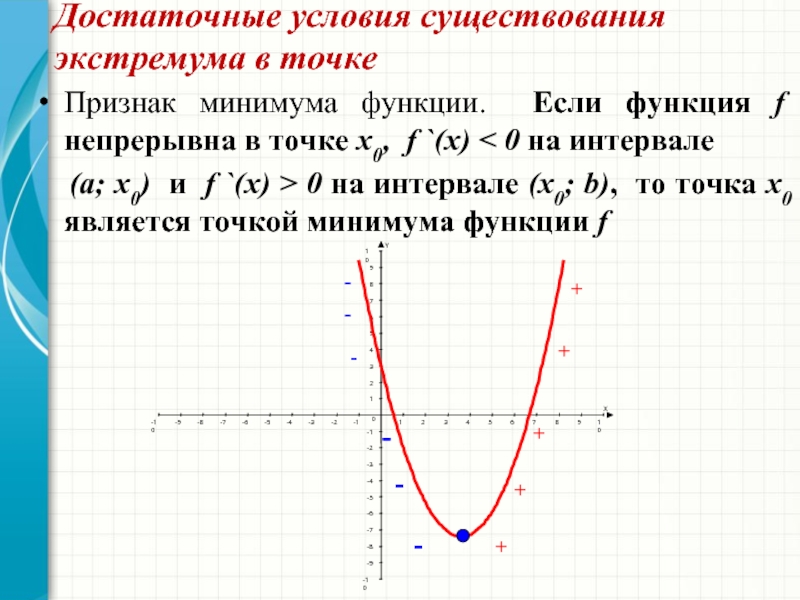
3) Возрастание, убывание и экстремумы
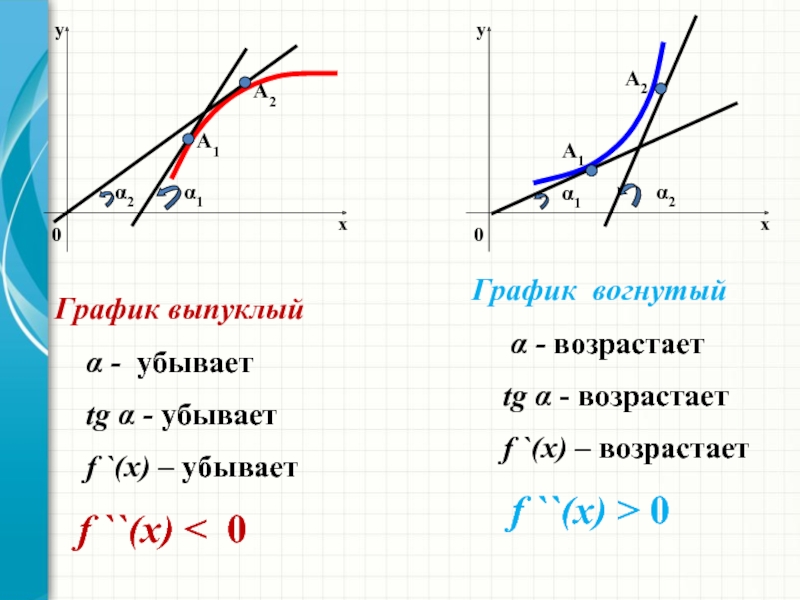
функции.4) Выпуклость, вогнутость и перегибы графика.





![Исследование функций и построение графиков функция y = f (x) называется возрастающей на отрезке [a, b],если для любой пары точек х и х', а ≤ х функция y = f (x) называется возрастающей на отрезке [a, b],если для любой пары точек х и х', а ≤ х](/img/thumbs/53bd43deae15b5b1f326c070284eac75-800x.jpg)