Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сфера, шар основные характеристики 11 класс
Содержание
- 1. Сфера, шар основные характеристики 11 класс
- 2. Окружность и кругЧасть плоскости, ограниченная окружностью, называется
- 3. Определение сферыСферой называется поверхность, состоящая из всех
- 4. ШарТело, ограниченное сферой, называется шаром.Центр, радиус и
- 5. Как изобразить сферу?R1. Отметить центр сферы (т.О)2.
- 6. Уравнение сферы(x – x0)2 + (y –
- 7. Задача Зная координаты центра С(2;-3;0), и
- 8. Взаимное расположение окружности и прямойrdЕсли d <
- 9. Сечение шара плоскостью есть круг. rВзаимное расположение
- 10. d = R, т.е. если расстояние
- 11. d > R, т.е. если расстояние от
- 12. Задача. Шар радиусом 41 дм пересечен плоскостью,
- 13. Свойство касательной.Касательная к окружности перпендикулярна к радиусу,
- 14. Признак касательной.ПланиметрияСтереометрияrЕсли радиус сферы перпендикулярен к плоскости,
- 15. № 592 Радиус сферы равен 112
- 16. OBМNCPAO1CAB№ 584 Все стороны треугольника АВС
- 17. Площадь сферыПлощадь сферы радиуса R:
- 18. Задача Найти площадь поверхности сферы,
- 19. Объем шара Vшара = 4/3ПR2
- 20. Объём шарового сегмента и шарового слояШаровой сегмент
- 21. Объём шарового сектораVш. сектора = 2/3ПR2hШаровой сектор
- 22. Скачать презентанцию
Окружность и кругЧасть плоскости, ограниченная окружностью, называется кругом. Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии r от данной точки. r – радиус; d – диаметр
Слайды и текст этой презентации
Слайд 1Урок-лекция
по теме:
Геометрия –11 класс
Сфера, шар
основные характеристики
Учитель математики
МБОУ «СОШ № 37» г. Новокузнецка
Слайд 2Окружность и круг
Часть плоскости, ограниченная окружностью, называется кругом.
Окружностью называется
геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном
расстоянии r от данной точки. r – радиус;
d – диаметр
Слайд 3Определение сферы
Сферой называется поверхность, состоящая из всех точек пространства, расположенных
на данном расстоянии (R) от данной точки (центра т.О).
Сфера –
тело полученное в результате вращения полуокруж-ности вокруг её диаметра.т. О – центр сферы
О
D – диаметр сферы – отрезок, соединяющий любые 2 точки сферы и проходящий через центр.
D = 2R
R – радиус сферы – отрезок, соединяющий любую точку сферы с центром.
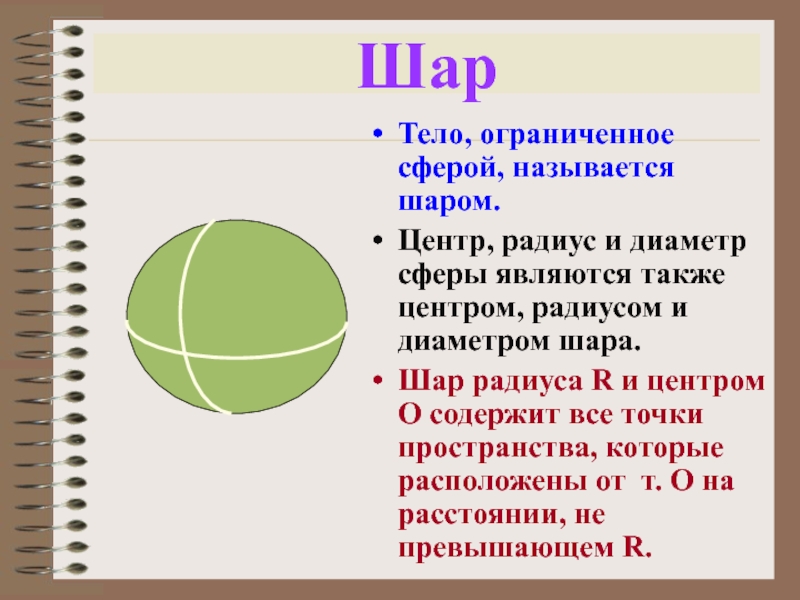
Слайд 4Шар
Тело, ограниченное сферой, называется шаром.
Центр, радиус и диаметр сферы являются
также центром, радиусом и диаметром шара.
Шар радиуса R и центром
О содержит все точки пространства, которые расположены от т. О на расстоянии, не превышающем R.
Слайд 5Как изобразить сферу?
R
1. Отметить центр сферы (т.О)
2. Начертить окружность с
центром в т.О
3. Изобразить видимую вертикальную дугу (меридиан)
4. Изобразить невидимую
вертикальную дугу5. Изобразить видимую гори-зонтальную дугу (параллель)
6. Изобразить невидимую горизонтальную дугу
7. Провести радиус сферы R
О
Слайд 6Уравнение сферы
(x – x0)2 + (y – y0)2 + (z
– z0)2 = R2
R
МС = R , или
МС2 = R2следовательно уравнение
сферы имеет вид:
уравнение окружности имеет вид:
(x – x0)2 + (y – y0)2 = r2
М
М(х;у;z),
C
C(x0;y0;z0)
Слайд 7Задача Зная координаты центра С(2;-3;0), и радиус сферы R=5, записать
уравнение сферы.
Решение
так, как уравнение сферы с
радиусом R и центром в точке С(х0;у0;z0) имеет вид (х-х0)2 + (у-у0)2 + (z-z0)2=R2, а координаты центра данной сферы С(2;-3;0) и радиус R=5, то уравнение данной сферы (x-2)2 + (y+3)2 + z2=25 Ответ: (x-2)2 + (y+3)2 + z2=25
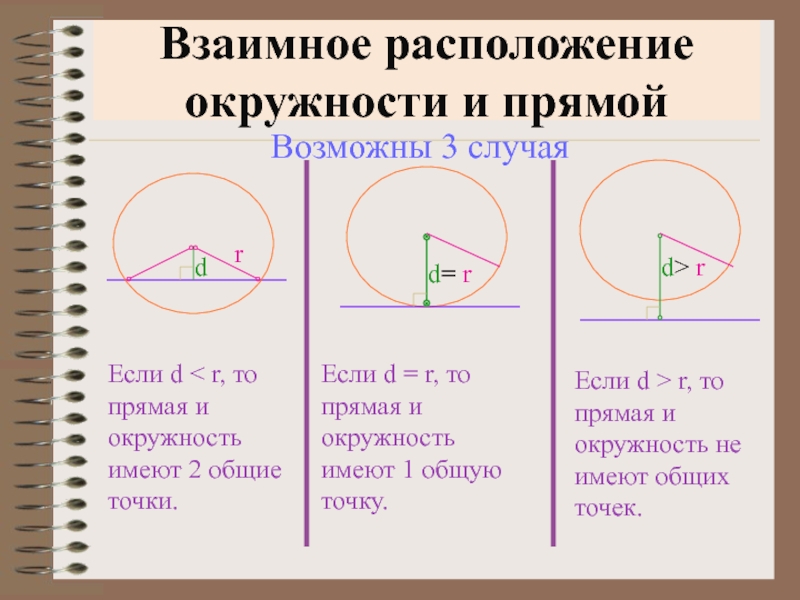
Слайд 8Взаимное расположение окружности и прямой
r
d
Если d < r, то прямая
и окружность имеют 2 общие точки.
d= r
d> r
Если d =
r, то прямая и окружность имеют 1 общую точку.Если d > r, то прямая и окружность не имеют общих точек.
Возможны 3 случая
Слайд 9Сечение шара плоскостью есть круг.
r
Взаимное расположение сферы и плоскости
Рассмотрим 1 случай
d < R, т.е. если расстояние от
центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружность радиусом r.r = R2 - d2
М
С приближением секущей плоскости к центру шара радиус круга увеличивается. Плоскость, проходящая через диаметр шара, называется диаметральной. Круг, полученный в результате сечения, называется большим кругом.
d
Слайд 10
d = R, т.е. если расстояние от центра сферы
до плоскости равно радиусу сферы, то сфера и плоскость имеют
одну общую точкуВзаимное расположение сферы и плоскости
Рассмотрим 2 случай
d
Слайд 11d > R, т.е. если расстояние от центра сферы до
плоскости больше радиуса сферы, то сфера и плоскость не имеют
общих точек.Взаимное расположение сферы и плоскости
Рассмотрим 3 случай
d
Слайд 12Задача. Шар радиусом 41 дм пересечен плоскостью, находящейся на расстоянии 9
дм от центра. Найти радиус сечения.
Дано:
Шар с центром в т.О
R=41
дмα - секущая плоскость
d = 9 дм
Найти: rсеч = ?
Решение:
Рассмотрим ∆ОМК – прямоугольный
ОМ = 41 дм; ОК = 9 дм; МК = r, r = R2 - d2
по теореме Пифагора: МК2 = r2 = 412- 92 = 1681 - 81=1600 отсюда rсеч = 40 дм
Ответ: rсеч = 40 дм
r
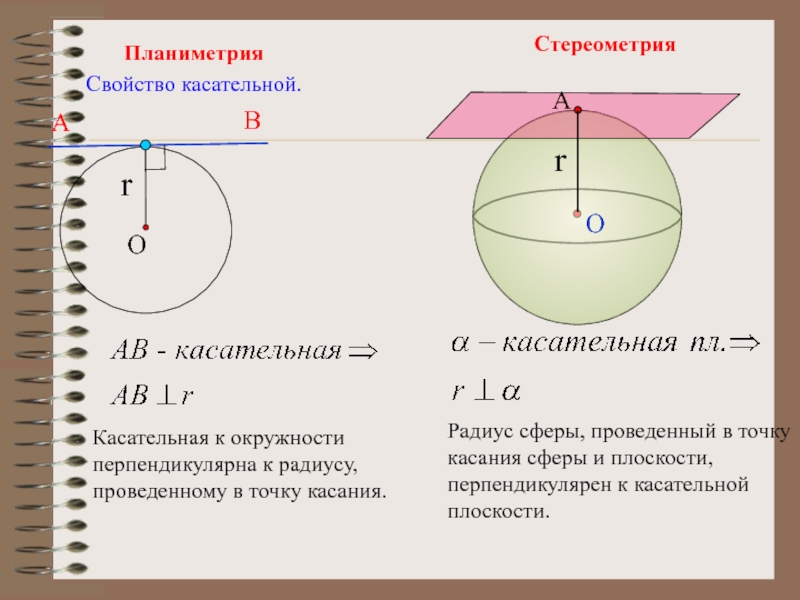
Слайд 13Свойство касательной.
Касательная к окружности перпендикулярна к радиусу, проведенному в точку
касания.
Планиметрия
Стереометрия
А
В
Радиус сферы, проведенный в точку касания сферы и плоскости,
перпендикулярен к касательной плоскости.
Слайд 14Признак касательной.
Планиметрия
Стереометрия
r
Если радиус сферы перпендикулярен к плоскости, проходящей через его
конец, лежащий на сфере, то эта плоскость является касательно к
сфере.Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
касательная
касательная пл.
Слайд 15
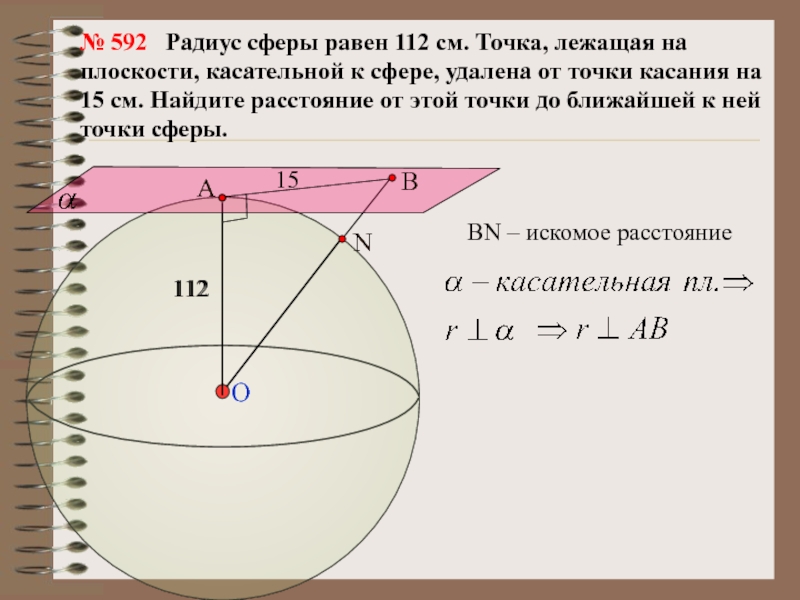
№ 592 Радиус сферы равен 112 см. Точка, лежащая
на плоскости, касательной к сфере, удалена от точки касания на
15 см. Найдите расстояние от этой точки до ближайшей к ней точки сферы.А
112
О
ВN – искомое расстояние
Слайд 16
O
B
М
N
C
P
A
O1
C
A
B
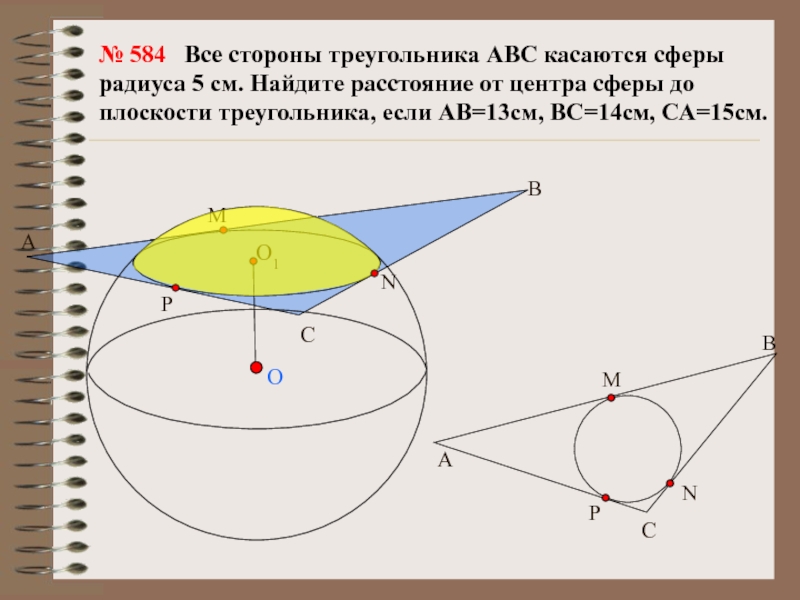
№ 584 Все стороны треугольника АВС касаются сферы радиуса
5 см. Найдите расстояние от центра сферы до плоскости треугольника,
если АВ=13см, ВС=14см, СА=15см.
Слайд 17Площадь сферы
Площадь сферы радиуса R: Sсф=4πR2
Сферу нельзя развернуть на плоскость.
Опишем около сферы многогранник, так
чтобы сфера касалась всех его граней. За площадь сферы принимается предел последовательности площадей поверхностей описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани
т.е.: Площадь поверхности шара равна учетверенной площади большего круга
Sшара=4 Sкруга
Слайд 18Задача
Найти площадь поверхности сферы,
радиус которой = 8 см.
Дано:
сфера
R = 8 см
Найти:
Sсф = ?
Решение:
Sсф = 4πR2
Sсф
= 4π 82 = 256π см2Ответ: Sсф = 256π см2
Слайд 20Объём шарового сегмента и шарового слоя
Шаровой сегмент – это часть
шара, отсекаемая от него какой-нибудь плоскостью.
Шаровой слой – это часть
шара, заключённая между двумя параллельными секущими плоскостями.Vш. сегмента=Пh2(R- 1/3h)
Vш. слоя=Vш.сег.1-Vш.сег.2
Основание сегмента
Высота сегмента (h)
Шаровой слой
Слайд 21Объём шарового сектора
Vш. сектора = 2/3ПR2h
Шаровой сектор – это тело,
полученное вращением кругового сектора, с углом, меньшим 90о, вокруг прямой,
содержащей один из ограничивающих круговой сектор радиусов.Шаровой сектор состоит из шарового сегмента и конуса
