Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Диагностика и развитие мышления школьников на уроках математики
Содержание
- 1. Диагностика и развитие мышления школьников на уроках математики
- 2. Учить надобно не мыслям, а мыслить…И. Кант
- 3. МышлениеТворческий, познавательный процесс, обобщенно и опосредованно отражающий отношения предметов и явлений, законы объективного мира
- 4. Мыслительные операцииАнализСинтезСравнениеАбстрагированиеОбобщение
- 5. Виды мышление, выделенные по различным основаниямПо формеНаглядно-действенноеНаглядно-образноеабстрактно-логическое
- 6. Важнейшие характеристики умаСамостоятельность мышленияКритичность мышленияГлубина мыслиГибкость мыслиПытливость ума
- 7. Схема формирования типов мышления в зависимости от характера обучения
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
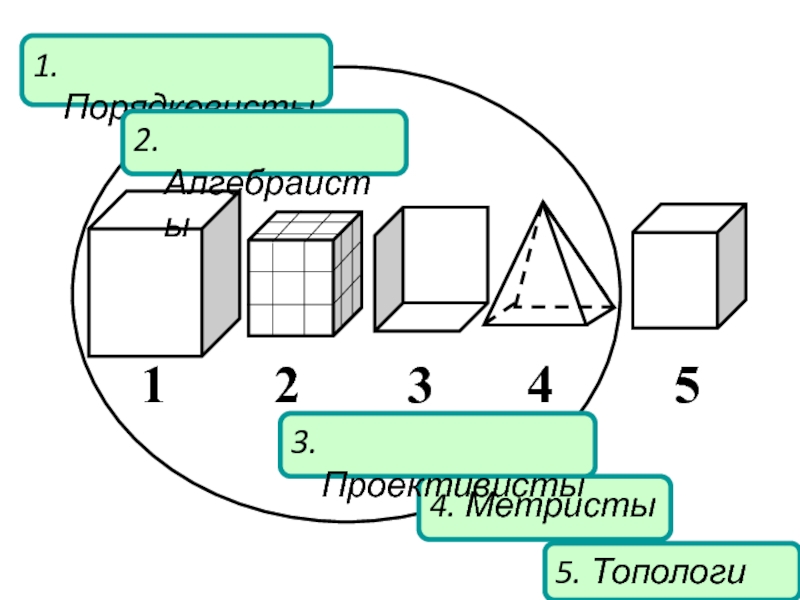
- 11. 5. Топологи1. Порядковисты4. Метристы3. Проективисты2. Алгебраисты
- 12. Как усваивается школьниками в зависимости от доминантного
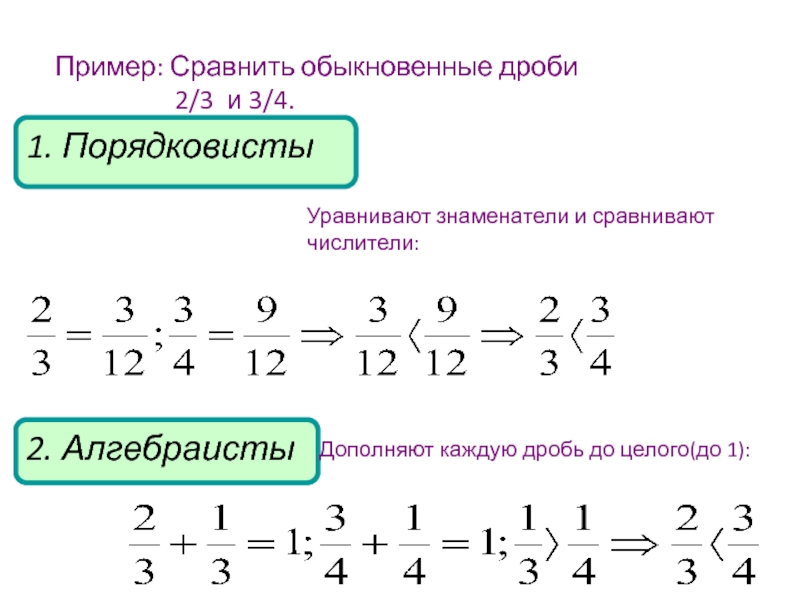
- 13. Пример: Сравнить обыкновенные дроби 2/3 и 3/4.
- 14. 4. Метристы5. ТопологиСтроят единичный отрезок, делят его
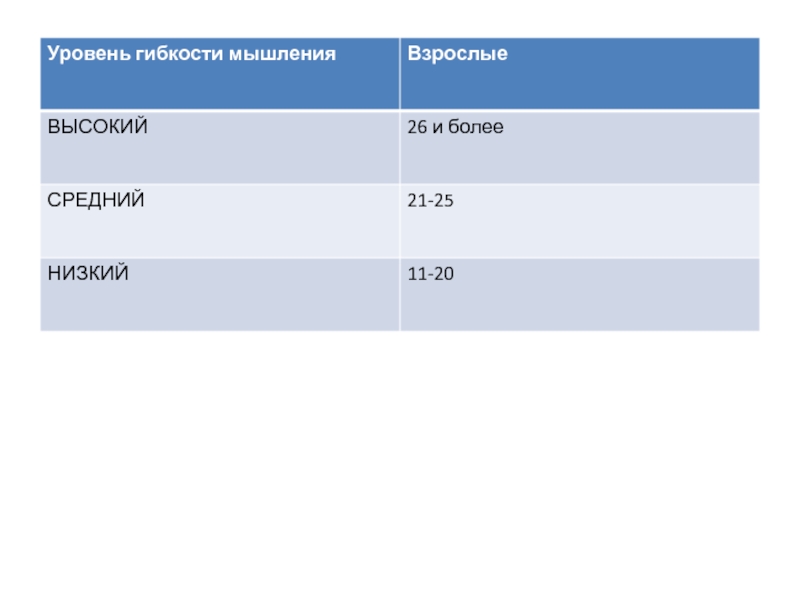
- 15. Методика «Исследование гибкости мышления» Позволяет определить
- 16. Слайд 16
- 17. Тест Липмана «Логические закономерности»2, 3, 4, 5,
- 18. Слайд 18
- 19. Методика «Закономерности числового ряда»Методика оценивает логический аспект
- 20. Методика «Исключение понятий»Методика предназначена для исследования способности
- 21. Методика «Выделение существенных признаков математических понятий»Цель -
- 22. Логические задачиПреподавателиВ пед. университете Смирнова, Лисичкина, Ежова,
- 23. Комплекс интеллектуальных игр для развития мышления учащихсяСоставление
- 24. Об организации игровых занятий для развития мышления,
- 25. Какого возраста могут быть игроки?От 11 до
- 26. Сколько детей должно быть в группе?Наиболее успешно
- 27. Используемая литература1.Тестирование детей/Автор составитель В. Богомолов Серия
- 28. Скачать презентанцию
Учить надобно не мыслям, а мыслить…И. Кант
Слайды и текст этой презентации
Слайд 1Диагностика и развитие мышления школьников на уроках математики
Составитель Тихвинская А.
В., преподаватель кафедры математического образования НИПКиПРО
Слайд 3Мышление
Творческий, познавательный процесс, обобщенно и опосредованно отражающий отношения предметов и
явлений, законы объективного мира
Слайд 5Виды мышление, выделенные по различным основаниям
По форме
Наглядно-действенное
Наглядно-образное
абстрактно-логическое
По характеру решаемых
задач
Теоретическое
Практическое
По степени развернутости
Дискурсивное
Интуитивное
По степени новизны и оригинальности
Репродуктивное
Продуктивное
Слайд 6Важнейшие характеристики ума
Самостоятельность мышления
Критичность мышления
Глубина мысли
Гибкость мысли
Пытливость ума
Слайд 12Как усваивается школьниками в зависимости от доминантного кластера понятие «алгебраическое
выражение»
«Тополог» « Алгебраическим называется выражение, включающее в себя числа и
буквы, связанные знаками действий»«Проективист» «Алгебраическим называется выражение подобное, например, предложению в русском языке: как в языке задаются соответствующие слова, знаки препинания, так и в алгебраическом выражении заданы числа, буквы и знаки действий между ними»
«Порядковец» «Алгебраическим можно назвать выражение , в котором числа и буквы взаимодействуют друг с другом по конкретным правилам, строго определяемым законами, зафиксированными знаками математических действий»
«Метрист» «Алгебраическое выражение представляет собою определенное количество букв, чисел и знаков действий (то, что можно записать с помощью одной или нескольких букв, чисел и знаков действий). При этом заменяя буквы числами, всегда можно найти его конкретное числовое значение»
«Алгебраист» «Алгебраическое выражение состоит из чисел, букв и знаков действий»
Слайд 13Пример: Сравнить обыкновенные дроби
2/3 и 3/4.
1. Порядковисты
2. Алгебраисты
Уравнивают знаменатели и
сравнивают числители:
Дополняют каждую дробь до целого(до 1):
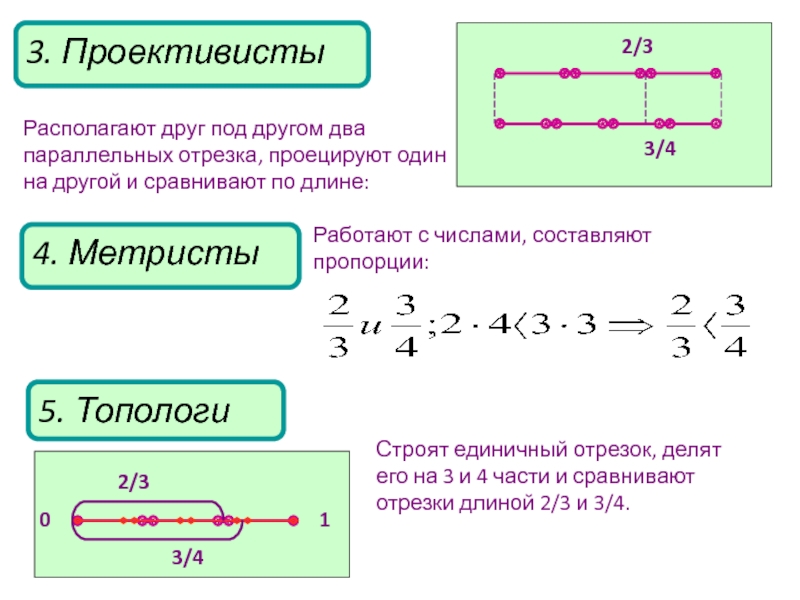
Слайд 144. Метристы
5. Топологи
Строят единичный отрезок, делят его на 3 и
4 части и сравнивают отрезки длиной 2/3 и 3/4.
Работают с
числами, составляют пропорции:3. Проективисты
Располагают друг под другом два параллельных отрезка, проецируют один на другой и сравнивают по длине:
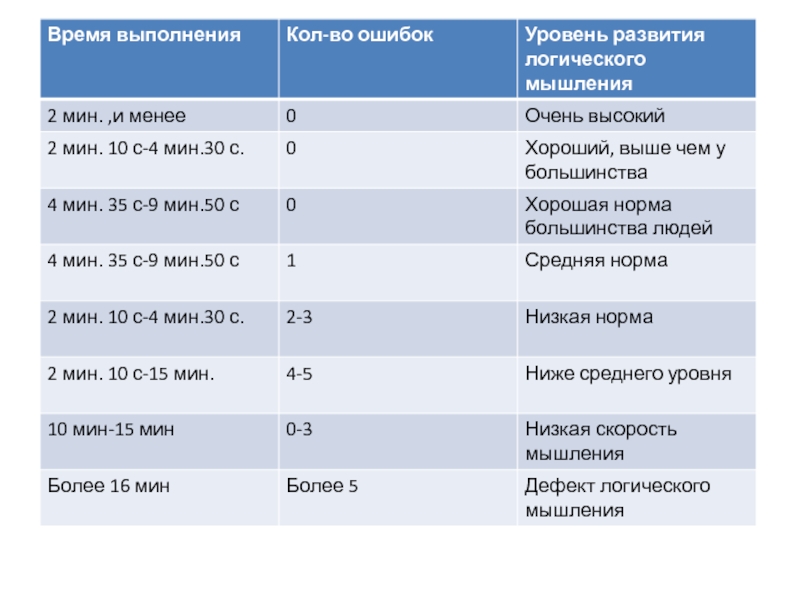
Слайд 15 Методика «Исследование гибкости мышления» Позволяет определить вариативность подходов, гипотез, исходных данных,
точек зрения, операций, вовлекаемых в процесс мыслительной деятельности. Время выполнения 3
минуты.Слайд 17Тест Липмана «Логические закономерности»
2, 3, 4, 5, 6, 7
6, 9,
12, 15, 18, 21
1, 2, 4, 8, 16, 32
4, 5,
8, 9, 12, 1319, 16, 14, 11, 9, 6
29, 28, 26, 23, 19, 14
16; 8; 4; 2; 1; 0,5
1; 4; 9; 16; 25; 36
21; 18; 16; 15; 12; 10
3; 6; 8; 16; 18; 36
Слайд 19Методика «Закономерности числового ряда»
Методика оценивает логический аспект мышления. Время выполнения
5 минут.
1) 24 21 19 18 15 13 _
_ 72) 1 4 9 16 _ _ 49 64 81 100
3) 16 17 15 18 14 19 _ _
4) 1 3 6 8 16 18 _ _ 76 78
5) 7 16 9 5 21 16 9 _ _ 1
6) 2 4 8 10 20 22 _ _ 92 94
7) 24 22 19 15 _ _
Слайд 20Методика «Исключение понятий»
Методика предназначена для исследования способности к классификации и
анализу. Задание - найти лишнее слово в каждом ряду. Время
выполнения 3 минуты.Василий, Федор, Семен, Иванов, Петр.
Дряхлый, маленький, старый, изношенный, ветхий
Скоро, быстро, поспешно, постепенно, торопливо
Лист, почва, кора, чешуя, сук
Ненавидеть, презирать, негодовать, возмущаться, понимать
Темный, светлый, голубой, яркий ,тусклый
Гнездо, нора, курятник, сторожка, берлога
Неудача, волнение, поражение, провал, крах
Успех, удача, выигрыш, спокойствие, неудача
Грабеж, кража, землетрясение, поджог, нападение
Молоко, сметана, сыр, сало, простокваша
Глубокий, низкий, светлый, высокий, длинный
Хата, шалаш, дым, хлев, будка
Береза, сосна, дуб, ель, сирень
Секунда, час, год, вечер, неделя
Смелый, храбрый, решительный, злой, отважный
Карандаш, ручка, рейсфедер, фломастер, чернила
Слайд 21Методика «Выделение существенных признаков математических понятий»
Цель - определить умение выделять
существенные признаки мат. понятий
1.Геометрия (фигура, точка, свойство, уравнение, теорема)
2. Уравнение
(корень, равенство, сумма, неизвестная, произведение)3. Планиметрия (плоскость, квадрат, прямоугольник, фигура, прямая)
4. Треугольник (вершина, катет, сторона, центр, перпендикуляр)
5. Сумма (слагаемое, равенство, плюс, делитель, множитель)
6. Периметр ( разность, сторона, сумма, фигура, прямоугольник)
7. Куб (угол, равенство, плоскость, сторона, вектор)
8. Дробь (делимое, делитель, частное, знаменатель, числитель)
9. Степень (корень, показатель, решение, основание, переменная)
10. Координата (плоскость, абсцисса, ось, ордината, прямая)
Слайд 22Логические задачи
Преподаватели
В пед. университете Смирнова, Лисичкина, Ежова, Петин, Рощин и
Кленов преподают философию, английский, немецкий, литературу, математику и биологию.
Преподаватели литературы
и биологии в студенчестве занимались художественной гимнастикой.2) Рощин старше Кленова, но стаж работы у него меньше, чем у преподавателя философии.
3) Студентками Смирнова и Лисичкина учились вместе в одном институте. Все остальные окончили пед. университет.
4) Кленов – отец преподавателя немецкого.
5) Преподаватель английского – самый старший из всех по возрасту и по стажу работы. Он работает в этом пед. университете с тех пор как окончил его.
6) Преподаватели биологии и математики его бывшие студенты.
7) Смирнова старше преподавателя литературы.
Кто какой предмет преподает?
Слайд 23Комплекс интеллектуальных игр для развития мышления учащихся
Составление предложений
Поиск общего
Исключение лишнего
слова
Поиск аналогов
Поиск противоположных предметов
Поиск предметов по заданным признакам
Поиск соединительных звеньев
Способы
применения предметаФормулирование определений
Выражение мысли другими словами
Перечень возможных причин
Перечень заглавий к рассказу
Сокращение рассказа
Построение сообщения по алгоритму
Факт (что произошло)-причины – повод - сопутствующие события - аналогии и сравнения-последствия
Кто – что – где – чем – зачем – как – когда (алгоритм Цицерона)
Слайд 24Об организации игровых занятий для развития мышления, воображения и памяти
школьников
Каковы исходные принципы построения занятий?
1. Использование на занятиях хорошо знакомого,
привычного для ребят материала.2. Взаимообмен различными подходами к выполнению заданий и тем самым значительное расширение диапазона познавательных процессов каждого из учащихся.
3. Интеллектуальная раскованность детей и общий положительный эмоциональный фон занятий.
Как можно оценить эффективность проведенных занятий?
Динамика успеха ребенка в выполнении самих игровых заданий.
Динамика успехов в выполнении традиционных интеллектуальных тестов.
Динамика общей успеваемости школьников и повышение их активности на уроках; анализ текущей успеваемости, наблюдение на уроках, беседы с учителями.
Слайд 25Какого возраста могут быть игроки?
От 11 до 17 лет, при
этом внутри тренинговой группы желательно собрать игроков одного возраста.
На какой
исходный уровень развития рассчитаны занятия?Развиваемые в ходе тренинга интеллектуальные качества являются универсальными. Сложность может варьироваться за счет изменения содержания.
В группе должны быть дети сходного или различного интеллектуального уровня ?
Сходный уровень – лучше ориентируются в ответах друг друга, проявляют большую инициативу, прогрессируют более или менее равномерно.
Различный уровень – задаются высокие стандарты ответов, есть возможность изучать и заимствовать интеллектуальные стратегии, опробуя их при выполнении последующих заданий.
Как определить исходный интеллектуальный уровень детей?
Слайд 26Сколько детей должно быть в группе?
Наиболее успешно группа работает при
числе игроков от 7 до 10.
Что делать с пассивными детьми?
Ненавязчивое
приглашениеТактика выжидания
Должен ли быть отсев и как с ним бороться?
От 25 до 28 % детей после 4-7 занятий отсеиваются.
На какое число занятий рассчитан тренинг?
Минимальное число занятий , при котором можно ожидать развивающего эффекта
в тренинге мышления 12-14 / 22-25
воображения 16-18 / 32 -35
памяти 8-10 / 20-22
Слайд 27Используемая литература
1.Тестирование детей/Автор составитель В. Богомолов Серия «Психологический практикум».-Ростов н/Д:
«Феникс», 2004.-352с.
2.Тихомирова Л. Ф Развитие интеллектуальных способностей школьника. Популярное пособие
для родителей и педагогов.- Ярославль: Академия развития, 1996.-240 с., ил.3. Заика Е. В. «Комплекс интеллектуальных игр для развития мышления учащихся» Вопросы психологии, № 6, 1990г